
|
|
Ожидаемые доходности и риск активов12 Доходность активов (ценных бумаг) Под инвестированием понимается любой процесс, имеющий целью сохранение и увеличение стоимости денежных или других средств. Средства, предназначенные для инвестирования, представляют собой инвестиционный капитал. Тот или иной вид инвестиционного капитала называется инвестиционным активом.
Финансовые активы, специальные контракты, определяющие взаимные обязательства сторон, участвующих в контракте, получили название ценных бумаг. Примеры ценных бумаг - акции, облигации, векселя, депозитные сертификаты. Каждая ценная бумага имеет свою стоимость на рынке ценных бумаг, причем стоимость ее меняется с течением времени.
Пусть ценная бумага куплена по некоторой цене. Будем ее называть начальной ценой. Продав на рынке ценную бумагу ее владелец получит определенный доход в размере стоимости ценной бумаги на момент ее продажи. Стоимость ценной бумаги на момент продажи ценной бумаги будем называть ее конечной ценой. Доход от операции купли-продажи за время ее владения будет разность между конечной и начальной ценой. Доход от изменения цены так же называют прирост капитала. Если конечная стоимость ценной бумаги уменьшилась по отношению к его начальной стоимости, то прирост капитала отрицательный.
Доход от владения ценной бумагой складывается не только от роста его стоимости, но и от текущего дохода. По облигациям это проценты, фиксируемые контрактом, а по акциям - дивиденды. Говоря о доходе необходимо указывать за какой промежуток времени он получен. Полный доход от владения ценной бумагой за некоторый период - сумма прироста капитала и текущего дохода за этот период. Для оценки полного дохода вводят такую характеристику как доходность за период. Доходность актива за период это отношение полного дохода за период к начальной стоимости актива. Доходность обычно измеряется в процентах, т.е. полученный результат умножается на 100%. Пример 1.1. Акция куплена в начале года за 40$. В конце года она продана за 50$. Дивиденды за год 10$. Найти годовую доходность в процентах. Решение Начальная цена - 40$, конечная цена - 50$. Прирост капитала - 50$-40$=10$. Текущий доход - 10$. Полный доход за год - прирост капитала + текущий доход = 10$+10$=20$. Доходность есть отношение полного дохода к начальной цене - 20/40=0,5 или 50%. Ответ: Годовая доходность - 50%. Пример 1.2. Акция куплена в начале года за 50$. В конце года она продана за 45$. Дивиденды за год 5$. Найти годовую доходность в процентах. Решение Начальная цена - 50$, конечная цена - 45$. Прирост капитала - 45$-50$=-5$. Текущий доход - 5$. Полный доход за год - прирост капитала + текущий доход = Ответ: Годовая доходность - 0%. Пример 1.3. Акция куплена в начале месяца за 20$. В конце месяца она продана за 15$. Дивиденды за месяц 0$. Найти месячную доходность в процентах. Решение Начальная цена - 20$, конечная цена - 15$. Прирост капитала - 15$-20$=-5$. Текущий доход - 0$. Полный доход за месяц - прирост капитала + текущий доход = =(-5)/20=-0,25 или -25%. Ответ: Месячная доходность - -25%.
Ожидаемые доходности и риск активов В портфельной теории Марковица значения доходностей актива рассматриваются как значения некоторой дискретной случайной величины. Будем обозначать ее - Рассмотрим некоторые характеристики дискретной случайной величины. Математическое ожидание случайной величины
дисперсия есть -
среднеквадратическое отклонение -
Математическое ожидание часто называют средним значением случайной величины - оно представляет собой число, вокруг которого “группируются” значения случайной величины. Дисперсия характеризует “степень отклонения” случайной величины от ее среднего значения. Из определения дисперсии видно, что она имеет размерность квадрата размерности величины В теории Марковица математическое ожидание есть формальный аналог понятия “ожидаемой доходности актива”, а дисперсия, или, что существу то же самое, стандартное отклонение служит мерой риска актива. Таким образом, каждому активу (если известен ряд доходностей актива) можно поставить в соответствие - дискретную случайную величину. Вычисляя математическое ожидание и дисперсию этой случайной величины мы получаем ожидаемую доходность и ожидаемый риск для актива.
Пример 2.1. Известен ряд ежемесячных доходностей акций AMBRND (в %) за 1987 год. Значения доходностей приведены в ниже. Вычислить ожидаемую доходность и риск. AMBRND - 17.694, 2.02, -3.713, -8.74, -0.518, 7.163,7.262, 16.877, -3.879, -22.556, -12.61, 19.463 Решение AMBRND - 17.694, 2.02, -3.713, -8.74, -0.518, 7.163,7.262, 16.877, -3.879, -22.556, -12.61, 19.463
Ожидаемая доходность акций 1.538583%. Для вычисления ожидаемого риска составим ряд значений 16,155417, 0.481417, -5.251583, -10.278583, -2.056583, 5.624417, 5.723417, 15.338417, -5.417583, -24.094583, -14.148583, 17.924417 Возведя в квадрат каждое значение получим ряд значений Ответ: Ожидаемая доходность 1.53%, ожидаемый риск - 152.47%. Задачи Ежемесячные доходности акций AMEX, CBS, EXXON за 1987 год приведены ниже. Найти их ожидаемые доходности и риск. 2.1. AMEX: 20.088, 8.824, 1.02, -8.403, -0.917, 2.044,7.664, 0.678, -3.367, -32.223, -7.254, 2.235 2.2. CBS: 9.941, 15.846, -5.435, 7.553, -0.458, 8.166, 11.325, 3.903, 11.619, -23.533, -9.558, 1.046 2.3. EXXON: 18.004, -4.199, 9.41, 1.02, 1.472, 7.184, 0.938, 6.906, -2.384, -12.339, -12.610, 3.741 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Значения этой случайной величины будем обозначать -
. Значения этой случайной величины будем обозначать -  . Пусть известны ее N значений, т.е.
. Пусть известны ее N значений, т.е.  .
. , (2.1)
, (2.1) (2.2)
(2.2) . (2.3)
. (2.3)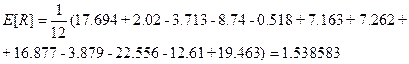
 .
. в %.
в %.