
|
|
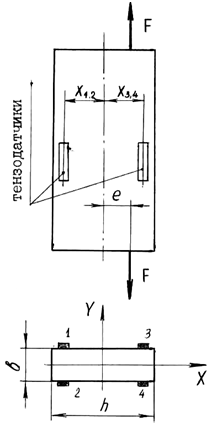
Порядок выполнения и обработка результатовДля проведения испытания используется машина ГРМ – 1А и опытный образец в виде бруса прямоугольного сечения. Для измерения деформации используются тензодатчики омического сопротивления. Тензодатчики попарно наклеиваются с каждой стороны параллельно оси образца на одинаковом расстоянии от нее (рисунке 20). После закрепления образца дается предварительная нагрузка и снимаются показания поочередно с 4-х датчиков, данные заносятся в таблицу журнала испытаний. Затем нагрузка увеличивается (приращение нагрузки ΔF), вновь снимаются показания датчиков, определяются приращения показаний ΔП для каждого датчика, средние приращения для групп датчиков ΔПср и полученное данные заносятся в таблицу. Зная тарировочный коэффициент Кσ, определяют напряжения в зоне наклейки датчиков от приращения нагрузки ΔF. Значения напряжений, полученные опытным путем, сравниваются с теоретическими значениями напряжений, найденными по формуле (21). Далее определяют процент погрешности опыта, строя эпюры распределения напряжений по сечению образца по данным, полученным экспериментально и теоретически, и дают выводы по выполненной работе.
Рисунок – 20 Схема нагружения образца и расположение датчиков
Контрольные вопросы 1. Какая деформация называется внецентренным растяжением (сжатием)? 2. Из каких простейших видов деформаций состоит сложная деформация внецентренного растяжения? 3. Какие допущения принимаются при решении задачи внецентренного растяжения (сжатия)? Какой вид при этом имеет формула напряжений? 4. Чем характерна нейтральная ось и какой вид имеет ее уравнение? Как определить ее положение в сечении? 5. Чему равны напряжения в центре тяжести сечения бруса? Как это доказать? 6. Как опытным путем определить нормальные напряжения в точках сечения бруса? Какие датчики при этом можно применять?
Лабораторная работа № 14 Испытание на устойчивость Цель работы – исследование явления потери устойчивости прямолинейной формы равновесия при осевом сжатии, проверить опытным путем справедливость формулы Эйлера.
Основные сведения У стержней, длина которых значительно больше поперечных размеров, при определенной величине осевой сжимающей силы происходит искривление оси. Это явление носит название продольного изгиба. Переход прямолинейной формы равновесия в криволинейную называется потерей устойчивости. Сжимающая сила, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической. Ее можно определить по формуле Эйлера
где: Е – модуль продольной упругости материала; l – длина стержня;
μ – коэффициент приведения длины, который зависит от способов закрепления концов стержня. Формула Эйлера применима лишь в том случае, если потеря устойчивости стержня происходит при напряжениях, меньших предела пропорциональности σпц, т.е. когда справедлив закон Гука
Здесь А – площадь поперечного сечения; λ=μ⋅l/imin – гибкость стержня;
– минимальный радиус инерции сечения.
Предельная гибкость, начиная с которой можно использовать формулу Эйлера, определяется по формуле
зависит лишь от физико-механических свойств и является постоянной для данного материала. Так, например, для стали Ст.З λпр = 100, для древесины λпр = 110, для чугуна λпр = 80, для дюралюминия λпр = 60. Стержни, у которых λ > λпр, называются стержнями большой гибкости. При меньших значениях гибкости (стержни средней гибкости) критические напряжения σкр > σпц определяются по эмпирическим формулам или соответствующим им таблицам (графикам). Например, формула Ясинского для определения критических напряжений имеет вид σкр = a – b λ, (25) где: a и b – эмпирические коэффициенты. Например, для стали Ст.3 a = 310 МПа, b = 1,14 МПа, для древесины (сосна) a = 28,7 МПа, b = 0,19 МПа. Эмпирические формулы, особенно для древесины, дают лишь приближенный результат. Для стержней малой гибкости, у которых σкр, подсчитанные по формуле Ясинского, получаются больше, чем опасные (предельные) напряжения, принимают: σкр = σт – для пластичных материалов; σкр = σв – для хрупких материалов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (22)
, (22) – минимальный момент инерции сечения;
– минимальный момент инерции сечения; . (23)
. (23)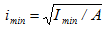
 , (24)
, (24)