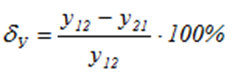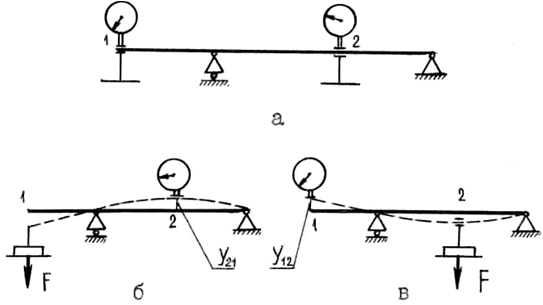
Порядок выполнения и обработка результатов

Опыты проводятся на настольной установке СМ-4, описанной в лабораторной работе № 9.

Проверка теоремы о взаимности перемещений (рисунок 13) выполняется следующим образом.

Рисунок – 13 Проверка теоремы о взаимности перемещений

В двух произвольных сечениях балки устанавливаются индикаторы и гиревые подвесы (сечения 1 и 2 рисунок 13, а). На индикаторе сечения 2 снимается начальный отсчет, балка нагружается в сечении 1 нагрузкой F и снимается отсчет индикатора, установленного в сечении 2 (см. рисунок 13, б). Разность данного и начального отсчетов равна величине прогиба у₂₁ в сечении 2. Затем балка разгружается.

Данные по F и у₂₁ заносятся в журнал испытаний. Далее на индикаторе, установленном в сечении 1, снимается начальный отсчет, балка нагружается в сечении 2 той же нагрузкой F и по разности отсчетов индикатора 1 определяется величина прогиба у₁₂ (см. рисунок 13, в).

Балка разгружается и данные по у₁₂ заносятся в журнал испытаний. Сопоставлением полученных данных по равенству (17) проверяется теорема о взаимности перемещений. Если равенство (17) не соблюдается, определяют процент погрешности

и делают выводы.

Используя теорему о взаимности перемещений, можно с помощью одного индикатора, закрепленного стационарно в сечении приложения нагрузки заданной расчетной схемы (рисунок 14), определить экспериментально перемещения балки в любом сечении и построить упругую линию балки.

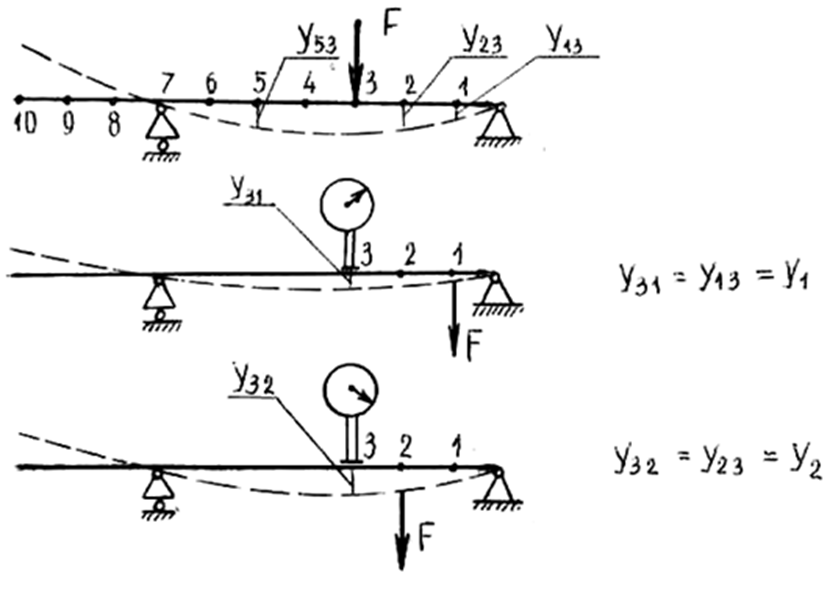
Рисунок – 14 Построение упругой линии балки

Индикатор линейных перемещений устанавливается в том сечении балки, в котором по расчетной схеме прикладывается заданная нагрузка. Один гиревой подвес размещается на консоли, второй – внутри пролета.

Определяются перемещения сечения, в котором установлен индикатор, при последовательном приложении заданной нагрузки F в расчетные точки 1 ... 10 (см. рисунок 14). Эта операция включает в себя установку гиревого подвеса в расчетную точку, снятие начального отсчета по индикатору, приложение заданной нагрузки F к гиревому подвесу, снятие отсчета индикатора и определение приращения отсчетов, равного определяемому перемещению. Для приложения нагрузки в сечениях, расположенных на консоли, используется второй гиревой подвес.

Согласно теореме о взаимности перемещений, эти перемещения будут равны перемещениям расчетных точек при приложении нагрузки F в сечении установки индикатора.

Полученные значения перемещений заносятся в журнал испытаний.

Для сравнения экспериментальных перемещений с теоретическими последние просчитываются для заданной расчетной схемы по универсальному уравнению в тех же сечениях. Расчет линейных перемещений может быть проведен на ЭВМ.

По результатам сравнения экспериментальных и теоретических значений прогибов необходимо сделать соответствующие выводы.

Контрольные вопросы

1. Сформулируйте теорему о взаимности работ и взаимности перемещений.

2. Поясните, как можно проверить теорему о взаимности перемещений в лабораторных условиях. Изложите порядок проведения работы.

3. Где можно использовать свойства теоремы о взаимности перемещений?

4. Как построить экспериментально линию прогибов балки, имея в наличии один индикатор линейных перемещений? Если предлагается несколько вариантов, то какой из них дает более точные результаты?

Лабораторная работа № 11

Определение лишней неизвестной в статически неопределимой балке

Цель работы – определить опытным путем лишнюю опорную реакцию однажды статически неопределимой балки и сравнить полученный результат с теоретическим.

Основные сведения

Система называется статически определимой, если внутренние усилия в ее элементах и реакции связей можно определить из условий равновесия статики. Система называется геометрически неизменяемой, если взаимные перемещения точек системы возможны лишь за счет деформации ее элементов.

То число внешних связей, при котором достигается геометрическая неизменяемость системы, называется необходимым числом связей. Всякую связь, наложенную сверх необходимой, называют дополнительной.

Наложение дополнительных связей на статически определимую систему увеличивает ее жесткость и прочность, но превращает ее в статически неопределимую систему, в которой реакции опорных связей и внутренние силовые факторы не могут быть определены с помощью уравнений равновесия статики. Степень статической неопределимости соответствует числу дополнительных связей.

Известно несколько методов расчета статически неопределимых систем. Наиболее простой и универсальный из них – метод сил, который заключается в следующем: устанавливается степень статической неопределимости системы, отбрасываются дополнительные связи, их действие заменяется неизвестными реакциями и записываются условия равенства нулю перемещений по направлению отброшенных связей.

Эти уравнения называются уравнениями совместности деформаций или каноническими уравнениями метода сил. Коэффициенты канонических уравнений, представляющие собой линейные или угловые перемещения, обычно определяются энергетическими методами.

Совместное решение уравнений статики и уравнений совместности деформаций дает возможность определить реакции всех связей.

При решении статически неопределимых задач вводятся следующие понятия: заданная система, основная система.

Любая рассматриваемая при решении статически неопределимая система называется заданной.

Основной системой называется любой из статически определимых (геометрически неизменяемых) вариантов рассматриваемой системы, полученный путем освобождения ее от лишних связей.

Рассмотрим вопрос определения лишней неизвестной для следующей заданной статически неопределимой системы (рисунок 15, a). Эта схема может быть осуществлена на настольной установке двухопорной балки СМ-4 (описание см. в лаб. работе №9).

Для иллюстрации определения лишней неизвестной в однажды статически неопределимой системе заданную систему (рисунок 15, а) выбираем такой, чтобы один из вариантов основной системы (см. рисунок 15, б) представлял собой, двухопорную балку с консолью, соответствующую расчетной схеме, рассмотренной в лабораторной работе №9.

Не нашли, что искали? Воспользуйтесь поиском по сайту: