
|
|
Определение реакций в кинематических парах
Определение реакций в кинематических парах начинаем с рассмотрения равновесия группы Ассура (2-3). На звенья этой группы действуют силы: движущая сила Fд, силы тяжести G3, G2, результирующие силы инерции Фu3, Фu2, реакция R03, заменяющая действие стойки 0 на ползун 3 и реакция R12, заменяющая действие кривошипа 1 на шатун 2. Силы, приложенные в точке B, приводим к одной силе F3. Величину этой силы определяем по формуле:
F3=+___+___+___=____ Н. Знак (+) показывает, что сила F3 направлена вверх. Условие равновесия группы (2-3) выражается следующим образом:
Реакцию R12 раскладываем на две составляющие: R Составляющую R Применительно к рассматриваемой схеме механизма это уравнение можно записать так: R откуда R R План сил (42) строим в масштабе: mF=___ Н/мм. Из произвольной точки Р последовательно откладываем вектора R По результатам расчета программы ТММ1 строим годограф реакции R12 в масштабе mR=_ Н/мм. Если в каждом из двенадцати положений ползуна отложить вектор R03 и соединить их конечные точки плавной кривой, то получим годограф реакции R03. По результатам расчета программы ТММ1 строим годограф реакции R03=R03(SB) в масштабе mR=_Н/мм, mS=_м/мм. Реакцию R32 в паре шатун – ползун определяем из условия равновесия ползуна:
и равенства:
или
Тогда R23X =R03 =_ H; R23Y =F3 =_ H; R23= R23= R32 =_ Н. По результатам расчета программы ТММ1 строим диаграмму реакции R32=R32(j1) в масштабе: mR=__ Н/мм.
Силовой расчет механизма 1 класса К кривошипу приложена сила тяжести G1, известная реакция
Чтобы кривошип мог совершать вращение по заданному закону, к нему со стороны отделенной части машинного агрегата должна быть приложена реактивная нагрузка в виде уравновешивающей силы Fy. Допустим, что неизвестная по модулю уравновешивающая сила приложена перпендикулярно кривошипу в точке А.
Определение сил тяжести Силу тяжести кривошипа определяем по формуле: G1=m1×g, (49) где m1 – масса кривошипа; g – ускорение силы тяжести. G1=_×9,81=_ Н. Определение реакций в кинематических парах Реакция R01 в паре кривошип-стойка и уравновешивающий момент My определяем из условия равновесия кривошипа ОА:
Силу Fy находим из условия: Fy× l1 –R21×h3=0. (51) Откуда Fy=R21×h3/l1; (52) Fy=_×_/_=_ Н. План сил строим в масштабе: mF=_ Н/мм. Из произвольной точки последовательно откладываем вектора R21, G1. Соединив конечную точку вектора G1 с начальной точкой вектора R21, получим вектор R01. Умножив полученную длину на масштабный коэффициент, получим: R01=___Н. По результатам расчета программы ТММ1 строим диаграмму реакции R01=R01(j1) в масштабе mR=__ Н/мм. Уравновешивающий момент My определяется по формуле: My=Fy×l1; (53) My=_×_=_Н×м. По результатам расчета программы ТММ1 строим диаграмму уравновешивающего момента Mу=Mу(j1) в масштабе: mM=___ Н×м/мм. Рычаг Жуковского С целью проверки правильности силового расчета механизма уравновешивающий момент My определяем с помощью рычага Жуковского. На план скоростей, предварительно повёрнутый на 90 градусов вокруг полюса, в соответствующие точки переносим все заданные силы, включая силы инерции и уравновешивающую силу Fy. Из условия равновесия плана скоростей, как рычага, определяем уравновешивающую силу Fy, прикладывая ее в точке a, считая ее как бы приложенной в точке A кривошипа, и направляем перпендикулярно линии кривошипа ОА. Таким образом: Fy×Pa+Фu2×h4+G2×h5-F3×Pb=0. (54) Откуда: Fy=(- Фu2×h4-G2×h5+F F Определяем величину уравновешивающего момента: M M Таблица 3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (41)
(41)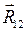 +
+  +
+  +
+  +
+  =0. (42)
=0. (42) – действующая вдоль оси звена AB и R
– действующая вдоль оси звена AB и R  – перпендикулярно звену AB.
– перпендикулярно звену AB. , F3+G2, Фu2. Через конечную точку вектора Фu2 проводим линию действия реакции R03, а через начальную точку вектора R
, F3+G2, Фu2. Через конечную точку вектора Фu2 проводим линию действия реакции R03, а через начальную точку вектора R  -линию действия силы R
-линию действия силы R  . Получим точку пересечения. Соединив конечную точку вектора Фu2с точкой пересечения, получим вектор R03. Соединив точку пересечения с конечной точкой вектора R
. Получим точку пересечения. Соединив конечную точку вектора Фu2с точкой пересечения, получим вектор R03. Соединив точку пересечения с конечной точкой вектора R  , получим вектор R12.Умножив соответствующие длины на масштабный коэффициент, получим: R03=_ H; R12=_ H.
, получим вектор R12.Умножив соответствующие длины на масштабный коэффициент, получим: R03=_ H; R12=_ H.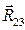 +
+  +
+ 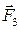 =0 (45)
=0 (45) , (46)
, (46) (47)
(47) (48)
(48) =_ Н;
=_ Н;
 . Неизвестная по значению и направлению реакция R01:
. Неизвестная по значению и направлению реакция R01: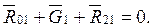
 =0. (50)
=0. (50) ×Pb)/Pa; (55)
×Pb)/Pa; (55) =( __×__ - __×__ + __×__ )/___=____ Н.
=( __×__ - __×__ + __×__ )/___=____ Н. =F
=F  ; (56)
; (56)