|
Векторное произведение двух векторов
Ориентация тройки некомпланарных векторов
Рассмотрим упорядоченную и некомпланарную тройку векторов  , ,  и и  . Откладываем их представители от произвольной точки О: . Откладываем их представители от произвольной точки О:    . Если из точки С видим, что кратчайший поворот вокруг точки О от точки А до точки В совершается против часовой стрелки, то упорядоченную тройку векторов . Если из точки С видим, что кратчайший поворот вокруг точки О от точки А до точки В совершается против часовой стрелки, то упорядоченную тройку векторов  , ,  и и  называем правой, а в противном случае левой. называем правой, а в противном случае левой.
Если две ориентированные тройки векторов обе правые или левые, то будем говорить, что они одной ориентации.
  
На рисунке показана правая тройка векторов (1) и левая тройка (2).
Представление о правой и левой тройке векторов можно получить, рассматривая первые три пальца, соответственно, правой и левой руки.
Замечание. Нетрудно заметить, что при перестановке двух векторов в упорядоченной тройке векторов  , ,  и и  или при замене одного вектора ему противоположным вектором, ориентация этой тройки векторов меняется на противоположную ориентацию. или при замене одного вектора ему противоположным вектором, ориентация этой тройки векторов меняется на противоположную ориентацию.
Определение. Под векторным произведением двух коллинеарных векторов понимаем нулевой вектор. Под векторным произведением двух неколлинеарных векторов  и и  понимаем новый вектор понимаем новый вектор  , который задается следующими условиями: , который задается следующими условиями:
1. |  | = | | = |  | | | |  |sinj, |sinj,
2.  ^ ^  , ,  ^ ^  , ,
3. Упорядоченная тройка векторов  , ,  , ,  – правая. – правая.
Обозначения:  = [ = [  , ,  ] или ] или  = =  ´ ´  . .
Свойства векторного произведения.
Свойство 1. [  , ,  ] = − [ ] = − [  , ,  ] . ] .
Доказательство. Так как угол j между векторами неориентированный, то правый и левый векторы рассматриваемого равенства имеют одинаковую длину |  | | | |  | sinj. | sinj.
Покажем, что направления рассматриваемых векторов одинаковое.
Действительно, [  , ,  ] ^ ] ^  и [ и [  , ,  ] ^ ] ^  . С другой стороны, [ . С другой стороны, [  , ,  ] ^ ] ^  и [ и [  , ,  ] ^ ] ^  . Следовательно, [ . Следовательно, [  , ,  ] êê [ ] êê [  , ,  ]. ].
Так как упорядоченная тройка векторов  , ,  , [ , [  , ,  ] – правая, то упорядоченная тройка векторов ] – правая, то упорядоченная тройка векторов  , ,  , [ , [  , ,  ] – левая. С другой стороны, упорядоченная тройка векторов ] – левая. С другой стороны, упорядоченная тройка векторов  , ,  , [ , [  , ,  ] – правая. ] – правая.
Следовательно,
[  , ,  ] ¯ [ ] ¯ [  , ,  ], а [ ], а [  , ,  ] −[ ] −[  , ,  ] . ] .
Векторы, имеющие одинаковую длину и одинаковое направление, равны. Свойство доказано.
Свойство 2. l[  , ,  ] = [l ] = [l  , ,  ] = [ ] = [  , l , l  ]. ].
Доказательство. Если l = 0 или   , то равенства выполняются, так как каждый из рассматриваемых векторов является нулевым вектором. , то равенства выполняются, так как каждый из рассматриваемых векторов является нулевым вектором.
Рассматриваем ненулевые случаи. Докажем, что l[  , ,  ] = [l ] = [l  , ,  ]. Для этого докажем равенство их длин и совпадение направлений. ]. Для этого докажем равенство их длин и совпадение направлений.
|l[  , ,  ]| = |l||[ ]| = |l||[  , ,  ]| = |l| | ]| = |l| |  | | | |  | sinj, где j – угол между векторами | sinj, где j – угол между векторами  и и  . .
|[l  , ,  ]| = |l ]| = |l  || ||  | sina, где a – угол между векторами l | sina, где a – угол между векторами l  и и  . .
Обратим внимание на то, что a = j, если l > 0 и a = p – j, если l < 0. В любом случае, sina = sinj и, следовательно, |l[  , ,  ]| = |[l ]| = |[l  , ,  ]|. ]|.
Рассмотрим направления этих векторов:
l[  , ,  ] [ ] [  , ,  ], если l > 0 и l[ ], если l > 0 и l[  , ,  ] ¯ [ ] ¯ [  , ,  ], если l < 0. ], если l < 0.
С другой стороны, если l > 0, то l   и [l и [l  , ,  ] [ ] [  , ,  ], а если ], а если
l < 0, то l  ¯ ¯  и [l и [l  , ,  ] ¯ [ ] ¯ [  , ,  ]. В том и другом случае получили: ]. В том и другом случае получили:
l[  , ,  ] [l ] [l  , ,  ]. ].
Свойство доказано.
Свойство 3. [  , ,  + +  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ]. ].
Доказательство. В случае, когда хотя бы один из данных векторов нулевой, равенство очевидно. Поэтому в дальнейшем считаем, что рассматриваемые вектора ненулевые. Доказательство разбиваем на три случая.
1. Рассмотрим случай, когда  ^ ^  , ,  ^ ^  и | и |  | = 1. Откладываем представители векторов | = 1. Откладываем представители векторов  , ,  , ,  и и  + +  от произвольной точки О: от произвольной точки О:   , ,  и и  . В плоскости ОВС рассмотрим поворот вокруг точки О на 90° по часовой стрелке, если смотреть из точки А. При этом образом точек О, В, С и D будут точки О, В¢, С¢ и D¢. Кроме того, мы получим правые тройки векторов . В плоскости ОВС рассмотрим поворот вокруг точки О на 90° по часовой стрелке, если смотреть из точки А. При этом образом точек О, В, С и D будут точки О, В¢, С¢ и D¢. Кроме того, мы получим правые тройки векторов  , ,  , ,  ¢, ¢,  , ,  , ,  ¢ и ¢ и  , ,  , ,  ¢. ¢.
В силу построения имеем
 ¢ = [ ¢ = [  , ,  ] , ] ,  ¢ = [ ¢ = [  , ,  ] и ] и  ¢ = [ ¢ = [  , ,  ] . ] .
Так как
 ¢ = ¢ =  ¢ + ¢ +  ¢, ¢,
то
[  , ,  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ]. ].
Таким образом,
[  , ,  + +  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ]. ].
Если вектор  не единичный, то его можно представить в виде не единичный, то его можно представить в виде  = | = |  | | 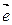 , где , где 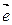 – единичный вектор, сонаправленный с – единичный вектор, сонаправленный с  . Тогда предыдущее равенство можно записать в виде . Тогда предыдущее равенство можно записать в виде
[ 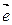 , ,  + +  ] = [ ] = [ 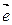 , ,  ] + [ ] + [ 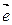 , ,  ]. ].
Умножая обе части равенства на |  |, получим: |, получим:
|  | [ | [ 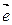 , ,  + +  ] = | ] = |  | [ | [ 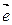 , ,  ] + | ] + |  | [ | [ 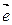 , ,  ] ]
и, соответственно,
[  , ,  + +  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ]. ].

2. Пусть условия случая 1 не выполнены. Тогда откладываем представители векторов  , ,  , ,  и и  + +  от произвольной точки О: от произвольной точки О:   , ,  и и  и через точку О проводим плоскость s, перпендикулярную направленному отрезку и через точку О проводим плоскость s, перпендикулярную направленному отрезку  . Спроектируем ортогонально на плоскость s точки В, С и D. При этом получим, соответственно, точки В0, С0 и D0. . Спроектируем ортогонально на плоскость s точки В, С и D. При этом получим, соответственно, точки В0, С0 и D0.
Как и в случае 1 находим
 ¢ = [ ¢ = [  , ,  0] , 0] ,  ¢ = [ ¢ = [  , ,  0] и 0] и  ¢ = [ ¢ = [  , ,  0] . 0] .
Так как
 ¢ = ¢ =  ¢ + ¢ +  ¢, ¢,
то
[  , ,  0] = [ 0] = [  , ,  0] + [ 0] + [  , ,  0]. 0].

( На рисунке показан только фрагмент с вектором  ) )
С другой стороны, [  , ,  0] = [ 0] = [  , ,  ] = ] =  ¢. ¢.
Действительно, вектор  ¢ перпендикулярен каждому из векторов ¢ перпендикулярен каждому из векторов  , ,  0 и 0 и  . Ориентация упорядоченных троек векторов . Ориентация упорядоченных троек векторов  , ,  0 , 0 ,  ¢ и ¢ и  , ,  , ,  ¢ – правая. Рассмотрим их длины. ¢ – правая. Рассмотрим их длины.
|[  , ,  ]| = | ]| = |  || ||  |sin j, где j – угол между векторами |sin j, где j – угол между векторами  и и  . .
|[  , ,  ]| = | ]| = |  || ||  0|. 0|.
Обозначим угол a между векторами  0 и 0 и  . Тогда sin j = cos a. . Тогда sin j = cos a.
С другой стороны,
|  |sin j = | |sin j = |  |cos a = | |cos a = |  0|. 0|.
Следовательно,
|[  , ,  0]| = |[ 0]| = |[  , ,  ]| = | ]| = |  ¢|. ¢|.
Аналогично,
|[  , ,  0]| = |[ 0]| = |[  , ,  ]| = | ]| = |  ¢|, ¢|,
и
|[  , ,  0]| = |[ 0]| = |[  , ,  ]| = | ]| = |  ¢|. ¢|.
Следовательно,
[  , ,  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ] ]
или
[  , ,  + +  ] = [ ] = [  , ,  ] + [ ] + [  , ,  ]. ].
Свойство доказано.
Замечание. Пусть  - упорядоченная ортонормированная тройка векторов. Тогда - упорядоченная ортонормированная тройка векторов. Тогда
[  , ,  ] = ] =  , ,  ] = ] =  , ,  ] = ] =  , ,  , ,  ] = ] =  , ,  , ,  ] = ] =  , ,   ] = ] =  , ,
[  , ,  ] = – ] = –  , [ , [  , ,  ] = – ] = –  , ,  ] = – ] = –  , ,
Свойство 4. Пусть в базисе {  } заданы векторы } заданы векторы  ( (  ), ),  ( (  ). Тогда ). Тогда
[  , ,  ] = ] =  . .
Доказательство. Доказанные свойства 1-3 позволяют векторно перемножать векторные многочлены по обычным правилам перемножения многочленов, не забывая при этом свойство антикоммутативности 1. Воспользуемся этими свойствами и предыдущим замечанием:
[  , ,  ] = [ ] = [   ] = [ ] = [  , ,  ] +[ ] +[  , ,  ] + [ ] + [  , ,  ] + +[ ] + +[  , ,  ] + [ ] + [  , ,  ] + [ ] + [  , ,  ] + [ ] + [   ] + [ ] + [   ] + [ ] + [   ] = ] =
=  , ,  ] + ] + 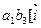 , ,  ] + ] +  , ,  ] + ] +  , ,  ] + ] +   ] + ] +   ] = ] =
=  – – 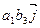 – –  + +  + +  – – 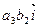 = =
=  ( (  – –  ) – ) –  ( (  – –  ) + ) +  ( (  – –  ) = ) =
=   – –   + +   = =  . .
Свойство доказано.
Свойство 5. Длина векторного произведения векторов  и и  численно равна площади параллелограмма, построенного на представителях данных векторов с общим началом. численно равна площади параллелограмма, построенного на представителях данных векторов с общим началом.
Доказательство. Если  || ||  , то параллелограмм вырождается, и его площадь рана нулю. При этом и [ , то параллелограмм вырождается, и его площадь рана нулю. При этом и [  , ,  ] = ] =  . Следовательно, свойство верно. . Следовательно, свойство верно.
 
Если данные векторы не коллинеарные, то |[  , ,  ] | = | ] | = |  | | | |  |sinj, но, с другой стороны, площадь параллелограмма также равна | |sinj, но, с другой стороны, площадь параллелограмма также равна |  | | | |  |sinj. |sinj.
Свойство доказано.
Пример 1. На представителях векторов  , ,  построен параллелограмм ABCD. Найти площадь треугольника ABD. построен параллелограмм ABCD. Найти площадь треугольника ABD.
Решение.
Ранее мы показали, что площадь параллелограмма можно находить, используя свойства векторного произведения двух векторов. Согласно этому свойству, имеем: 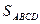 = | = |  |. Находим векторное произведение |. Находим векторное произведение
 , ,
откуда
 . .
Следовательно,  . .
Ответ: 12,5 (кв.ед).
Пример 2. Пусть  , ,  , ,  , ,  - произвольные векторы. Доказать, что - произвольные векторы. Доказать, что  . (1) . (1)
Решение.
Заметим, что левая и правая части данного равенства представляют собой числа. Покажем, что эти числа представимы в виде одного выражения.
Рассмотрим следующие случаи:
1. Векторы  и и  коллинеарные. коллинеарные.
Тогда  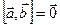 по определению векторного произведения. по определению векторного произведения.
 . .
Таким образом, левая часть равенства (1) равна  и равна ее правой части. и равна ее правой части.
2. Векторы  и и  неколлинеарные. неколлинеарные.
Тогда 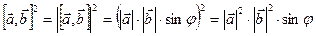 , где , где  - угол между векторами - угол между векторами  и и  . Итак, . Итак,
 . (2) . (2)
 . .
 . (3) . (3)
Из равенств (2) и (3) получаем, что левая часть равенства (1) равна  , ,
и равна ее правой части.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ,
,  и
и  . Откладываем их представители от произвольной точки О:
. Откладываем их представители от произвольной точки О: 

 . Если из точки С видим, что кратчайший поворот вокруг точки О от точки А до точки В совершается против часовой стрелки, то упорядоченную тройку векторов
. Если из точки С видим, что кратчайший поворот вокруг точки О от точки А до точки В совершается против часовой стрелки, то упорядоченную тройку векторов 


 и
и  , который задается следующими условиями:
, который задается следующими условиями: ,
,  . В плоскости ОВС рассмотрим поворот вокруг точки О на 90° по часовой стрелке, если смотреть из точки А. При этом образом точек О, В, С и D будут точки О, В¢, С¢ и D¢. Кроме того, мы получим правые тройки векторов
. В плоскости ОВС рассмотрим поворот вокруг точки О на 90° по часовой стрелке, если смотреть из точки А. При этом образом точек О, В, С и D будут точки О, В¢, С¢ и D¢. Кроме того, мы получим правые тройки векторов  ,
,  ,
,  ,
,  ,
, 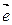 , где
, где 
 . Спроектируем ортогонально на плоскость s точки В, С и D. При этом получим, соответственно, точки В0, С0 и D0.
. Спроектируем ортогонально на плоскость s точки В, С и D. При этом получим, соответственно, точки В0, С0 и D0.
 - упорядоченная ортонормированная тройка векторов. Тогда
- упорядоченная ортонормированная тройка векторов. Тогда ,
,  ,
,  ] =
] =  ,
,  ] =
] =  ,
,  ,
,  ,
,  ,
, 
 ] = –
] = –  ),
),  ). Тогда
). Тогда .
.
 ] = [
] = [  ,
,  ] +[
] +[  ] + [
] + [  ] + +[
] + +[  ,
, 
 ,
, 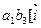 ,
,  ,
,  ,
, 

 –
– 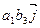 –
–  +
+  +
+  –
– 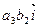 =
= –
–  ) –
) –  –
–  ) +
) +  –
–  ) =
) =
 –
–  +
+  =
= 

 ,
,  построен параллелограмм ABCD. Найти площадь треугольника ABD.
построен параллелограмм ABCD. Найти площадь треугольника ABD.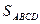 = |
= |  |. Находим векторное произведение
|. Находим векторное произведение ,
, .
. .
. ,
,  ,
,  ,
,  - произвольные векторы. Доказать, что
- произвольные векторы. Доказать, что  . (1)
. (1)
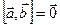 по определению векторного произведения.
по определению векторного произведения. .
. и равна ее правой части.
и равна ее правой части. , где
, где  - угол между векторами
- угол между векторами  . (2)
. (2) .
. . (3)
. (3) ,
,