Исследование системы линейных уравнений общего вида. Теорема Кромекера-Капелли.

Теорема о базисном миноре. Базисным называют минор порядка равного рангу матрицы отличной от нуля. Строчки(столбцы) образующие базисный минор и называемые базисными линейно зависимы. Любая строка(столбец) может быть выражена линейной комбинацией базисных. Теорема Кромекера-Капелли. Для того, чтобы система уравнений была совместна Н. И Д., чтобы ранг основной матрицы был равен рангу расширенной матрицы.

Схема исследования: 1-Rang главной матрицы = Rang расширенной матрицы => система совместна; 2-Сравнить число неизвестных и Rang. Если R=r, то система имеет единственное решение. Если они равны, то система имеет единственное решение. Если число неизвестных больше чем ранг, то система имеет бесчисленное кол-во решений и система неопределенная; 3-Выбрать базисный минор. Неизвестные коэффициенты, при которых входят в базисный минор, назовём базисными неизвестными. Именно они подлежат определению, все остальные назовём свободными неизвестными; 4-Переписать систему уравнений относительно базисных неизвестных. Т. е. Оставить их в первых частя уравнения, свободные неизвестные со своими коэффициентами перенести в правые части уравнения, уравнения, коэффициенты которых не входят в базисный минор – отбросить. Новых решений они не дадут.

11. Однородная система уравнений, нетривиальная совместность однородной системы.

Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной. Однородная система уравнений всегда совместна. Ранг основной матрицы равен рангу расширенной матрицы, которая отличается наличием столбца свободных членов(нулевого столбца). Для того, чтобы система была нетривиального совместна необходимо и достаточно, чтобы её ранг был меньше числа неизвестных. Если матрица квадратная, то Н. и Д., чтобы её определитель был равен нулю.

Модель Леонтьева. Продуктивные модели Леонтьева.

Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями. Математическая модель Леонтьева позволяет анализировать связь между отраслями. Xj – объём продукции i отрасли, валовый выпуск продукции i-ой отрасли. Xij – Объём продукции I отрасли, потребляемой j-ой при производстве. Yj – объём продукции i-ой отрасли предназначенной для реализации – конечный продукт. Работает балансовый принцип связи различных отраслей промышленности. Валовый выпуск i-ой отрасли должен быть равен сумме объемов потребления в производственной и непроизводственной сферах.

Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i-й

отрасли должен быть равен сумме объёмов потребления в производственной и непроизводственной сферах.

В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеют вид:

Xi=Xi1+Xi2+…+Xin+Yi. Эти уравнения называются соотношениями баланса. Модель Леонтьева называется продуктивной, если система имеет неотрицательное решение.

Основные понятия теории многочленов. Теории Безу. Основная теория алгебры. Разложение многочленов на многочлены.

, где n – целое число, коэффициенты – константы – коэффициенты многочлена. Высшая степень x – называется степенью многочлена. Два многочлена равные если равны их соответствующие коэффициенты(коэф. При одинаковых степенях x). Корнем многочлена называют такое значение x, при котором многочлен образуется в ноль. Теорема Безу.При делении многочлена от x на двучлен x- получается остаток равный значению многочлена при x= 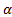. 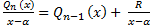, где остаток 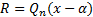. Следствие: Если – корень многочлена, то многочлен делится на x- без остатка. Основная теорема алгебры.Всякий многочлен имеет по крайней мере один корень. 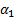Пусть – корень многочлена . – таким образом многочлен n-ой степени может быть представлен в виде произведения n-линейных множителей , где – корни многочлена и const. . Разложение многочлена на линейные множители 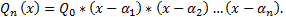Если многочлен имеет целые корни, то они содержатся среди делителей свободного члена многочлена. Если корни многочлена равны, то они называются кратными и тогда разложение многочлена можно представить в общем виде.

Не нашли, что искали? Воспользуйтесь поиском по сайту: