
|
|
Методы решения системы n уравнений с n неизвестными: матричный, метод Крамера.12 Матрицы. Матрицы частного вида. Матрица -прямоугольная таблица, имеющая n строк и m столбцов. Виды матрицы: строчная, столбец, квадратная, единичная матрица, нулевая, треугольная. У матрицы есть главная и побочная диагонали. Сложение матриц, умножение на число, перемножение матриц. Матрицы одинаковых размеров равны, если равны их соответствующие элементы. Суммой матриц A и B одинаковых размеров называется матрица тех же размеров, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц. Произведением числа на матрицу называют матрицу каждый элемент которой получен из исходной умножением на это число. Произведением матрицы A, имеющей m строк и n столбцов и m столбцов на матрицу B, имеющую n строк и p столбцов называется матрица C, имеющая m строк и p столбцов, каждый элемент которой равен сумме парных произведений элементов строки на соответствующие элементы столбца второй. Определители и их свойства. Определитель n-го порядка – число соответствующее квадратной матрице и полученное путем её преобразование по определенному правилу. Свойства: 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером. 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. 3. Определитель равен нулю, если имеет нулевую строку(столбец), имеет равные строки или пропорциональные. 4. Постоянный множитель строки(столбца) можно выносить за знак определителя. 5. Сумма парных произведений элементов некоторой строки(столбца) на алгебраическое дополнение другой строки равна нулю. 6. Если элементы некоторой строки определителя можно представить суммой двух слагаемых, то определитель можно представить суммой определителей, у которых элементы рассматриваемой строки равны соответствующим слагаемым. 7.Величина определителя не изменится, если к элементам некоторой строки(столбца) прибавить элементы другой строки умноженные на константу. 8.Треугольный определитель относительно главной диагонали равен произведению элементов стоящих на главной диагонали. Минор и алгебраическое дополнение элемента. Методы вычисления определителей. Разложение определителя по строкам и столбцам. Минором n-го порядка называется определитель, получаемый из исходной матрицы выделением произвольных строк и столбцов. Алгебраическое дополнение – минор, взятый со знаком, зависящим от номера строки и столбца. Определитель равен сумме произведений элементов любой строки (или любого столбца) определителя на их алгебраические дополнения. Невырожденная матрица, обратная матрица. Невырожденная матрица – квадратная матрица n-го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной. Матрица называется обратной, если при перемножении её и исходной матрицы мы получим единичную матрицу, она должна быть не вырожденной. 6. Ранг матрицы. Элементарные преобразования. Рангом матрицы называется наивысший порядок миноров этой матрицы, отличных от нуля. Элементарные преобразования: 1-перемена местами строк; 2-умножение всех элементов строки на const; 3-прибавление к элементам одной строки элементов другой строки умноженных на const; 4- отбрасывание нулевой строки. Системы линейных уравнений. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. В матричном виде система линейных уравнений представляется в виде столбца коэффициентов при неизвестных A, самого столбца неизвестных X и столбца свободных членов B. Методы решения системы n уравнений с n неизвестными: матричный, метод Крамера. Решение системы уравнений – это такой набор значений неизвестных, который удовлетворяет всем уравнениям системы. Система уравнений называется совместной, если она имеет решение и несовместной, если решений нет. Совместная система уравнений называется определенной, если решение единственное и неопределенной, если решений множество. Матричный способ решения. Столбец неизвестных получим , если столбец свободных членов умножим на матрицу обратную главной. Метод Крамера. Если главный определитель системы уравнений отличен от нуля, то система имеет единственное решение, определяемое по формулам Крамера Метод Гаусса. Суть метода состоит в том, чтобы путем применения элементарных преобразований главную матрицу системы привести к верхней правой треугольной относительно главной диагонали, причём на главной диагонали должны быть единицы. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
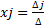 ,
,  – побочный определитель, получаемый из главного заменой j столбца на столбец свободных членов. Если главный определитель равен нулю: если все побочные определители равны нулю, то система будет неопределенной – множество решений; если существует
– побочный определитель, получаемый из главного заменой j столбца на столбец свободных членов. Если главный определитель равен нулю: если все побочные определители равны нулю, то система будет неопределенной – множество решений; если существует