
|
|
Ломаная линия, длина ломаной линии, периметр многоугольникаОпираясь на понятие отрезка, учащихся знакомят с ломаной линией (1 кл., с.38). Для этого по образцу, данному учителем, предлагают учащимся построить линию из палочек или бумажных полосок. Учитель дает название новой линии. Можно изготовить также модель ломаной, «сломав» на глазах у детей на части тонкую лучинку или кусок проволоки. На доске изображают иногда ломаную с помощью цветной нити, натянутой между несколькими кнопками - «точками», не лежащими на одной прямой. Учащиеся чертят ломаные линии на доске и в тетрадях: ставят 3 (4, 5 и т. д.) точки, не лежащие на одной прямой, и соединяют их отрезками. Каждый раз дети подсчитывают, сколько отрезков (звеньев) содержит ломаная линия и сколько у нее вершин. Учащиеся строят из палочек (полосок бумаги, кусочков проволоки) ломаную линию, находят ее начало (начало первого отрезка) и конец (конец последнего отрезка). Затем учащихся знакомят с измерением ломаных линий таким способом: измерить звенья ломаной и сложить полученные длины. Чтобы дети усвоили понятие длины ломаной линии, необходимо включить достаточное количество заданий в нахождении длины ломаных линий, которые содержат различное число звеньев. Понятие о периметре многоугольника в III классе даётся в процессе решения конкретной задачи на нахождение длины замкнутой ломаной линии. Сначала включают задачи на нахождение периметра многоугольников с неравными сторонами, в процессе решения которых закрепляется понятие о длине ломаной линии. Например, учащимся раздаются вырезанные из бумаги многоугольники или начерченные на карточках треугольники, четырехугольники и т. п. и дается задание найти сумму длин сторон данных фигур. Можно предложить построить многоугольники по точкам, не лежащим на одной прямой, соединить их последовательно отрезками, обозначить и раскрасить полученный многоугольник, а потом измерить стороны и найти сумму их длин. Затем специально рассматривается нахождение периметра равносторонних многоугольников, а также нахождение периметра прямоугольника. Периметр этих фигур дети находят сначала, как и на предыдущем этапе: измеряют каждую сторону и складывают полученные числа. Обращается внимание учащихся на равенство сторон, и учащиеся сами догадываются, что при нахождении суммы длин сторон равностороннего треугольника, квадрата и других многоугольников с равными сторонами достаточно измерить одну сторону, а затем умножить ее длину на число сторон многоугольника. При нахождении периметра прямоугольника достаточно узнать его длину и ширину (т. е. основание и высоту), затем умножить каждое из этих чисел на 2 и полученные произведения сложить. Здесь учащиеся, кроме геометрических знаний, закрепляют также и арифметические знания. Опираясь на чертеж, они подмечают, что можно поступить и по-другому: найти сумму длин смежных сторон, а затем умножить эту сумму на 2. Сравнивая полученные записи, например: 4-2+6-2 =20 (см) и (4 + 6)-2 = 20 (см), дети устанавливают, что во втором случае умножали сумму на число, а в первом - каждое слагаемое умножали на это число и результаты складывали. Так как использованное свойство умножения суммы на число известно детям, то они убеждаются в правильности своих рассуждений при нахождении периметра прямоугольника. В дальнейшем систематически решают задачи на вычисление периметра, а также задачи, им обратные, например: 1) Чему равна сторона квадрата, если сумма длин всех его сторон равна 2 дм 4 см? Начертите такой квадрат. 2) Участок квадратной формы с трех сторон обнесен забором, а одной стороной примыкает к дому, длина которого 9 м. Какова длина забора? 3) В треугольнике одна из сторон равна 10 см, а две другие равны между собой. Периметр треугольника 24 см. Какова длина каждой из равных сторон треугольника? При решении таких задач полезно выполнять чертеж на доске (хотя бы схематически). Наряду с решением готовых задач рекомендуется предлагать учащимся задания на составление подобных задач с геометрическим содержанием (подобрать и вставить в условие пропущенные числовые значения; составить задачу, обратную решенной задаче; составить задачу по данному решению и т. п.). В процессе выполнения таких заданий формируется понятие периметра многоугольника и умение находить его, а также развиваются пространственные и геометрические представления.
МЕТОДИКА ИЗУЧЕНИЯ ВЕЛИЧИН План 3.1. Общая характеристика методики изучения величин. 3.2.Время, порядок, задачи изучения темы. 3.3.Методика изучения величин. 3.1. Величина, так же как и число, является основным понятием курса математики начальных классов, в задачу которого входит формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое, прежде всего, связано с измерением. В I—IVклассах учащиеся получают представление о таких величинах, как длина, масса, емкость, время, площадь, и о единицах их измерения. В процессе решения задач они знакомятся с ценой, количеством, стоимостью, скоростью, временем, расстоянием и др. Формирование представлений о той или иной конкретной величине и оспособах ее измерения имеет свои особенности, тем не менее,целесообразно выделить общие этапы, которые имеют место при изучении каждой из величин и, ориентируясь на которые, учитель организует деятельность учащихся: 1 Формирование понятий о величине как свойстве окружающих объектов (выяснение и уточнение имеющихся у детей представлений о данной величине (обращение к опыту ребенка), сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок). 2. Знакомство с единицей измерения данной величиныи с измерительным прибором. 3. Формирование измерительных умений и навыков, измерение «на глаз». 4. Сложение и вычитание однородных величин, выраженныхв единицах одного наименования (в связи срешением задач). 5. Знакомство с новыми единицами измерения величины втесной связи с изучением нумерации по концентрам, перевод однородных величин, выраженных в единицах одних наименований, в другие, перевод величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот. 6. Сложение и вычитание величин, выраженных в единицах двух наименовании 7. Умножение и деление величинына число. С целью формирования представленийо разного рода величинах проводятся практические работы, используются специальные задания, применяются демонстрационные и индивидуальныенаглядные средства, при этом варьируются коллективные, индивидуальные и групповые формы работы на уроке. Учащиеся усваивают основные признакипонятия «величина» впроцессе выполнения различных практических заданий познавательного характера при широком использовании проблемных ситуаций. Знакомство с величинами и единицами их измерения имеет не только практическое значение: оно предоставляет большие возможности для формирования умения видеть проблему и находить пути ее решения, тем самым, способствуя развитию познавательных способностей учащихся. Время и порядок изучения единиц измерения величин
Методика изучения величин Длина
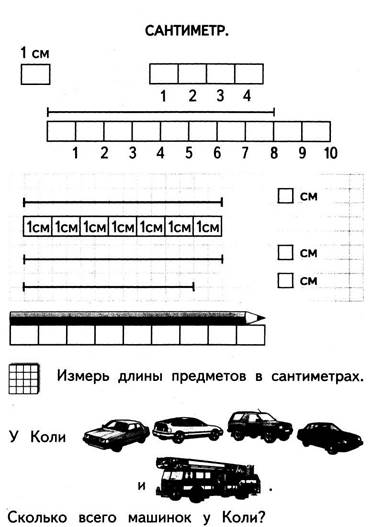
На первом этапе учитель выясняет, какие представления имеют учащиеся об изучаемой величине. С этой целью можно, например, показать два карандаша одного цвета, но разной длины и попросить учащихся охарактеризовать их. Умело направляя ответы детей с помощью наводящих вопросов, следует обратить их внимание именно на признак длины и добиться, чтобы они не только ответили, что один из карандашей длиннее, а другой короче, но и попытались доказать это, например, путем приложения карандашей друг к другу. Учитель варьирует подобные задания, используя при этом различные предметы, модели, рисунки, стремясь добиться того, чтобы учащиеся осознали, что предметы обладают свойством иметь длину и что их, например карандаши, можно сравнивать по этому признаку путем наложения, приложения и на глаз. Использование мерок для сравнения длин отрезков подготавливает учащихся к осознанию самого процесса измерения. Например, на доске начерчены два отрезка (90 см и 120 см). При этом они расположены так, что дать обоснованный ответ о том, какой из отрезков длиннее (короче), нельзя. (Способ наложения или приложения в этом случае не применим.). Учитель показывает ученикам планочку длиной 30 см, называет ее меркой и предлагает с ее помощью сравнить длины отрезков. Учащиеся самостоятельно укладывают планку сначала по длине одного отрезка, затем другого. Получают результат: 3<4 — и делают соответствующий вывод: первый отрезок короче, а второй длиннее. Аналогичное задание выполняют с другой планкой (15 см). Получают: 6<8 — и делают тот же вывод: первый отрезок короче второго. Затем учитель предлагает уложить первую планку по длине второго отрезка (она укладывается 4 раза), а вторую — по длине первого (укладывается 6 раз). Получается: 6>4. «Мы получили, что первый отрезок длиннее второго. Может быть, мы раньше делали неправильный вывод?» — спрашивает учитель. Созданная проблемная ситуация поможет учащимся осознать тот факт, что для сравнения длин отрезков необходимо пользоваться одной меркой. Это подготовит их к пониманию того, что числовое значение величины зависит от единицы измерения. Усвоение этого продолжается в процессе различных упражнений. Используя групповую форму работы на уроке, можно провести, например, такую практическую работу. На каждой парте модель отрезка (синего цвета) и две мерки (одна красного, а другая зеленого цвета). Учитель дает задание: «Ученики, сидящие слева, измеряют отрезок красной меркой, а сидящие справа — зеленой». В процессе измерения получаются разные числовые значения величины. Это позволяет учителю задать проблемный вопрос: «Разве может быть так: измерялся один и тот же отрезок, а числа получились совсем разные? В чем дело? Была допущена ошибка?» (Учащиеся должны осознать, что причина разных ответов — в использовании разных мерок при измерении одного и того же отрезка.) Можно предложить и такое задание: «Трое учеников измеряли один и тот же отрезок (отрезок предварительно вычерчивается в тетрадях). В результате первый из них получил в ответе 8, второй — 4, а третий — 2. Почему так могло получиться и кто из них прав?» Дети должны ответить, что первый принял за единицу измерения длину одной клеточки, второй — длину двух клеточек, а третий — длину четырех клеточек. Каждый из измерявших был бы прав, если бы указал в ответе единицу измерения. Учитель может сделать на доске такую условную запись: 8□, 4□□, 2 □□□□. Аналогичным заданием является измерение длины класса шагами или длины доски разными мерками. В результате практических работ учащиеся подводятся к выводу о необходимости введения единицы измерения длины. В качестве первой единицы измерения длины вводится сантиметр.
М.1, ч.1, с.60
Прежде чем ознакомить детей с линейкой и с правилами измерения длин отрезков с помощью этого инструмента, учитель предлагает ученикам ряд заданий: - измерение данного отрезка с помощью модели сантиметра путём укладывания на отрезке и подсчёта числа шагов; - изготовление и измерение отрезка с помощью неоцифрованной линейки; - нанесение шкалы на неоцифрованную линейку; - измерение ею длин отрезков, ознакомление с правилами измерения. Выполнение таких заданий позволяет предупредить главную ошибку при измерении отрезков: прикладывание к началу отрезка деления линейки с цифрой 1. Учащиеся упражняются в сложении и вычитании длин, выраженных в единицах одного наименования, в процессе решения задач на увеличение и уменьшение длины отрезка, на разностное сравнение, на нахождение суммы длин отрезков. Введение новых единиц длины — дециметра и метра осуществляется в процессе практической деятельности; соотношения между единицами длины закрепляются путем упражнений.
Масса В концентре «Десяток» учащиеся знакомятся с массой и единицей ее измерения — килограммом. При изучении этой темы необходимо особенно внимательно отнестись к терминологии. Дело в том, что до последнего времени при измерении массы с помощью чашечных весов было распространено неудачное использование слова «вес». Масса и весне одно и то же. Вес представляет собой силу, т. е. произведение массы на ускорение. Поэтому вместо вопроса: «Сколько весит предмет?» — следует приучить детей к такой форме вопроса «Какова масса предмета?» Эта форма вопроса принята теперь и в учебниках математики, начиная с I класса. В методике формирования представленияо массеможно выделить этапы, о которых шла речь ранее. Прежде всего, необходимо выяснить, какие представления имеются у детей о массе, и уточнить их. Для этого учитель может, например, создать такую ситуацию. Поставить на стол два одинаковых по цвету и размеру кубика (их можно изготовить один из дерева, другой из картона). Никаких внешних признаков различия учащиеся немогут обнаружить. Учитель подчеркивает, что различие между ними все-таки существует (учащиеся заинтересованы и пытаются угадать, в чем оно). У кого-то возникает желание рассмотреть кубики поближе, взять их в руки. Подняв кубики, они сразу же дают ответ: «Этот кубик тяжелее (легче)». Учитель уточняет, что со словами «легче» и «тяжелее» связано такое свойство предметов, как м а с с а . Вместо слов «предмет легче» или «предмет тяжелее» в математике принято говорить «масса предмета меньше» или «масса больше».
Рис. 1 Рис. 2 Затем учитель предлагает каждому из вызванных учеников взять в руки две книги (которые незначительно отличаются массой) — одну в левую руку, а другую в правую — и определить, какая из книг тяжелее. Выслушав различные мнения, учитель подчеркивает, что, оказывается, не всегда можно сравнить массы предметов, просто взяв их в руки. В таких случаях нужно воспользоваться простейшим прибором — чашечными весами. Учитель показывает весы, изображает их схематически на доске (рис. 1) и разъясняет принцип их использования при сравнении масс предметов. Необходимые навыки закрепляются в процессе упражнений. Внимание учеников фиксируется на положении стрелок при пустых чашках весов, а затем после того, как на них положены предметы. Учитель сообщает, что, так же как и для измерения длины, для измерения массы необходима единица измерения. Такой единицей является килограмм. Учитель показывает гири в 1 кг, 2 кг, 5 кг. Учащиеся выполняют упражнения по взвешиванию предметов, в процессе чего они не только расширяют свои представления о величинах, но и лучше усваивают другие вопросы курса математики, в частности совершенствуют свои вычислительные навыки. С этой целью предлагается такое задание: «Подумайте, какие предметы (какой массы) следует поставить на правую чашку весов (рис. 2), чтобы чашки весов были в равновесии». (На наборном полотне или на фланелеграфе размещены карточки, изображающие предметы различной массы: 2 кг, 3 кг, 5 кг, 1 кг и т. д.).
М.1, ч.2, с. 34
В процессе решения задач на нахождение суммы, остатка, на разностное сравнение и др. учащиеся упражняются в сложении и вычитании масс, выраженных в единицах одного наименования.
Емкость
С этой величиной и единицей ее измерения — литром учащиеся знакомятся в I классе. Никаких других единиц емкости вначальных классах не вводится. Поэтому такие этапы, как переход от одних единиц измерения к другим, сложение и вычитание величин, выраженных в единицах двух наименований, при изучении емкости отсутствуют. При ознакомлении учащихся с емкостью и ее единицей — литром можно, например, использовать следующие проблемные ситуации: 1. На столе учителя стоят два сосуда с водой: один узкий, другой широкий (уровень воды в обоих сосудах одинаков), два пустых стаканчика разной емкости (обозначим их № 1 и № 2), а также посуда для переливания. Учитель предлагает выяснить с помощью мерки № 1, в каком сосуде больше воды. Учащиеся устанавливают, что в широком сосуде помещается 10 таких мерок воды, а в узком только 5. Делается соответствующий вывод. Затем с той же целью используется мерка № 2. В широком сосуде помещаются 4 такие мерки воды, а в узком — 2. Делается вывод. После этого учитель предлагает измерить количество воды в широком сосуде с помощью мерки № 2, а в узком — с помощью мерки № 1. Обсуждение результатов подводит учащихся к выводу, что для сравнения количества воды в сосудах необходимо пользоваться единой меркой. Полезно и здесь провести сопоставление: так же как длину измеряем сантиметром, массу — килограммом, емкость будем измерять единицей емкости — литром. 2. Два сосуда с водой: один широкий, другой узкий, по при этом уровень воды в узком сосуде выше, чем н широком Учитель задает вопрос: «В каком сосуде больше воды?» Ответы противоречивы. Нужно решить проблему: как убедиться, в каком из сосудов больше воды? Учащиеся сами предлагают использовать в качестве мерки третий сосуд. Им будет интересно, если окажется, что и в тот и в другой сосуд налито одинаковое количество воды. Учитель подводит итог: при сравнении емкостей не всегда можно полагаться на ощущения — предположение следует проверять измерением. После введения единицы измерения емкости решаются разного рода практические задачи, например: «В одном сосуде 5 л воды, а в другом 3 л. Что нужно сделать, чтобы воды в сосудах стало поровну?» (Можно, например, перелить из первого сосуда во второй 1 л воды, тогда в каждом сосуде станет по 4 л. Или из первого вылить 2 л. И т. д.) «В одном сосуде 3 л воды, а в другом на 2 л больше. Как сделать, чтобы воды во втором сосуде было больше на 1 л?» Так же как и первая, задача требует от ребенка проведения предварительных рассуждений, которые должны предвосхитить практический результат. Учащиеся могут предложить долить в первый сосуд 1 л воды; отлить из второго сосуда 1 л; долить в первый сосуд 2 л, а во второй 1 л. Каждый из предложенных способов проверяется практически, т. е. сводится к простым упражнениям в измерении емкости. Предложенные задачи вызывают у детей больший интерес, нежели просто задание измерить с помощью литровой банки количество воды в сосуде.
Время
В соответствии с программой знакомство с этой величиной и единицами ее измерения осуществляется во II- IV классах. Однако, учитывая сложность процесса формирования временных представлений, необходимо с I класса вести работу в этом направлении. В I классе учащиеся имеют дело с временными понятиями в силу практической необходимости записать число и месяц, определить количество дней в неделе и месяце, длительность урока и перемены и т. п. Во II классе изучаются такие единицы времени, как час, минута; в III классе - год, месяц, сутки, в IV — секунда и век. Знакомство с единицами времени способствует уточнению временных представлений детей. Эффективным приемом формирования представлений о единицах времени является использование различных занимательных упражнений, например такого. Учитель предлагает ученикам хлопнуть в ладоши ровно через минуту после того, как хлопнет он. (Многие дети уже знают, что нужно досчитать до 60.) Вызывает у детей интерес и работа с календарем. В учебнике приводится большое количество заданий, которые могут при этом использоваться. В процессе их выполнения дети усваивают количество месяцев в году, дней в неделе и их последовательность. Большую роль в формировании представлений о единицах времени играют задачи на пропорциональную зависимость между такими величинами, как производительность, общая выработка и время, скорость и время, расстояние и время. В IV классе обобщаются знания детей о единицах времени и их соотношения. С этой целью используются такие задания: а) Вырази:
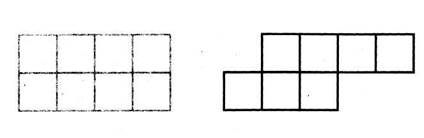
б) Вырази в более крупных единицах времени: 48 ч, 96 ч, 240 мин, 600 мин. Площадь Методика формирования представлений оплощади фигуры строится в соответствии с общей методикой формирования представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное — большее или меньшее — место на плоскости. Для разъяснения рассматриваемого понятия используются демонстрационные или индивидуальные модели различных фигур. Рис. 3
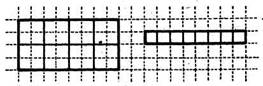
Рис. 4 Путем наложения их друг на друга учащиеся устанавливают, что площади первой и второй фигур одинаковы, а площадь четвертой меньше площади пятой, так как вся четвертая фигура помещается внутри пятой, и т. д. Учитель может предложить выписать номера фигур, расположив их в порядке возрастания площадей. В процессе таких упражнений уточняются представления детей о площади. После этого учитель может раздать ученикам листы клетчатой бумаги, на которых изображены различные фигуры, например фигуры, представленные на рисунке 4, и предложить сравнить площади этих фигур. Учащиеся сами догадываются, что для этого нужно сосчитать число клеток в каждой фигуре. Фигура, содержащая большее число клеток, имеет большую площадь. Можно предложить учащимся и такой вариант рисунка, чтобы при сравнении площадей изображенных на нем фигур появилась возможность выбрать другую мерку, например треугольник. Следует обратить внимание учащихся на тот факт, что при сравнении площадей необходимо пользоваться одной и той же меркой. Для этого можно взять демонстрационные модели фигур, каждая из которых разбита на квадраты разных размеров. Учитель предлагает посчитать число квадратов в каждой фигуре. Число квадратов оказывается одинаковым. - Можно ли утверждать, что площади данных фигур одинаковы? (Нет. Квадраты разные.) Полезно предложить также и задание, аналогичное тому, которое учащиеся выполняли, когда знакомились с длиной отрезка: «Трое учеников измеряли площадь одной и той же фигуры. В результате первый из них получил в ответе 8, второй — 4, а третий — 2. Почему так могло получиться и кто из них правильно измерил фигуру?» (Фигура предварительно
Рис. 5 чертится в тетради)
Рис. 6 Учащиеся должны указать на то, что каждый мальчик пользовался своей меркой. Учитель предлагает покрасить эти мерки в разные цвета. Такого рода задания подводят учащихся к осознанию необходимости введения общепринятой единицы площади 1 кв. см (квадрат со стороной, равной одному сантиметру). У каждого ученика должна быть модель квадратного сантиметра. Для того чтобы учащиеся освоили процесс измерения площади, полезно раздать им геометрические фигуры и предложить измерить их площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры — значит, узнать, сколько квадратных сантиметров она содержит. Учащиеся практически убеждаются в том, что укладывать модель квадратного сантиметра в фигуре долго и неудобно — гораздо удобнее использовать прозрачную бумагу, на которую нанесена сетка из квадратных сантиметров. Таким образом, учащиеся знакомятся с палеткой и правилами пользования ею, упражняются в определении площадей фигур с ее помощью. При определении площади прямоугольника необходимо также широко использовать практический метод.
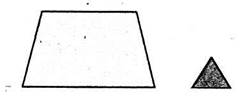
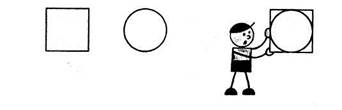
М. 3, ч. 1, с. 68 ПЛОЩАДЬ. ЕДИНИЦЫ ПЛОЩАДИ Классная доска висит на стене. Можно сказать, что площадь классной доски меньше, чем площадь этой стены. Ковёр лежит на полу и полностью его закрывает. Площадь ковра и площадь пола равны. Площадь четырёхугольника больше, чем площадь треугольника. Это видно на глаз. Сравнить площади круга и квадрата на глаз трудно. В таком случае используют способ наложенияфигур.
Круг весь поместился внутри квадрата. Значит, площадь круга ... , чем площадь квадрата, а площадь квадрата ... , чем площадь круга. Часто бывает, что способом наложения сравнить площади фигур нельзя. В этом случае можно подсчитать квадраты с одинаковой площадью, на которые разбита каждая фигура, и сравнить полученные числа.
Это поможет учащимся осознать тот факт, что найти площадь прямоугольника — значит узнать, сколько квадратных сантиметров в нем содержится. Однако найти число этих квадратных сантиметров можно рациональнее: путем умножения длины на ширину. При введении новой единицы площади — квадратного дециметра можно поступить следующим образом: нарисовать на доске прямоугольник и предложить учащимся измерить его площадь, пользуясь двумя моделями — квадратного сантиметра и квадратного дециметра. Учащиеся убеждаются практически, что использование квадратного сантиметра для измерения площади данной фигуры нерационально. Гораздо удобнее пользоваться большей меркой — квадратным дециметром. У каждого ученика должна быть модель квадратного дециметра, разбитая на квадратные сантиметры. Учащиеся самостоятельно устанавливают соотношение между данными единицами площади: 1 кв. дм = 100 кв. см. При знакомстве с квадратным метром необходимо иметь его демонстрационную модель, разбитую на квадратные дециметры. Соотношения между единицами площади закрепляются в процессе выполнения различных упражнений.
Арифметические действия с величинами Рассматривается сложение и вычитание однородных величин, умножение и деление величины на число. Приведем пример различного объяснения того, как выполнено действие 42 м 65 см + 26 м 83 см = 69 м 48 см: 1) 4265 2) 42 м 65 см + + 2683 или 26 м 83 см 6948 см 69 м 48 см 69 м 48 см Однако в любом случае дети должны понимать, что сложение и вычитание длины, массы и т. д. выполняется так же, как сложение и вычитание многозначных чисел. Аналогично для умножения и деления величины на число.
4. МЕТОДИКА ИЗУЧЕНИЯ ДРОБЕЙ В соответствии с программой по математике в начальных классах должна быть проведена подготовка к изучению дробей в последующих классах. Это значит, в начальных классах надо создать конкретные представления о доле и дроби. С этой целью npедусматривается в III классе ознакомить детей с долями, записью, научить сравнивать доли на наглядной основе, решать задачи на нахождение доли числа и числа по его доле. В IV классе ознакомить с дробями, их записью, научить сравнивать доли и дроби. Все названные вопросы раскрываются на наглядной основе. 4.1.Ознакомление с долями (М. 3, ч.1, с.96-99). Ознакомить детей с долями - значит сформировать конкретные представления о долях, т. е. научить детей образовывать доли практически. Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть; чтобы получить одну пятую долю отрезка, надо разделить его на пять равных частей и взять одну такую часть. Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги; можно использовать рисунки фигур, выполненные на бумаге или в диапозитивах (круги, прямоугольники, треугольники, бруски, отрезки и т. п.). Очень важно, чтобы пособия были не только у учителя, но и у каждого из учащихся. Правильные представления о долях, а позднее о дробях будут сформированы тогда, когда ученики будут своими руками получать, например, половину круга, квадрата и т. п., четверть отрезка и т. п. Покажем, как можно ознакомить детей с долями. У каждого из учащихся и у учителя несколько одинаковых кругов, прямоугольников (квадратов). Возьмите два одинаковых круга. Один из них paзделите на 2 равные части (показывает, как надо перегнуть и как разрезать круг).
Это целый круг, а это половина круга иначе говорят, одна вторая доля круга. Сколько вторых долей в целом круге? (2.) Покажите их. Возьмите квадрат. Как получить одну вторую долю, или половину квадрата? (Разделить его на дне равные части и взять одну такую часть.) Выполняйте. Учащиеся могут это сделать разными способами, например: разрезать квадрат по диагонали и получить два равных треугольника или же разрезать по средней линии, тогда получатся два прямоугольника. Некоторые учащиеся могут предложить и другие способы деления квадрата на две равные части (см. рис.)
Как получили одну вторую часть круга? (Разделили круг на две равные части и взяли одну такую часть.) Как получили одну вторую долю квадрата? Как иначе называют одну вторую долю круга, квадрата? (Половина круга, половина квадрата.) Сколько половин круга в целом круге? (2.) Учащиеся накладывают половины круга на целый круг. Доли записывают с помощью двух чисел. Одна вторая доля круга, квадрата обозначается так: Учащиеся записывают на половинах круга « Так же образуются доли При этом учащиеся должны уяснить, что для получения, например, Для закрепления этих знаний и умений учащимся предлагаются различные задания. Это, прежде всего, задания в назывании и записи долей. Назовите и запишите, какая доля квадрата (круга) отрезана (закрашена, заштрихована). Можно предлагать самим детям изобразить какую-либо долю отрезка (круга, квадрата и др.) и записать эту долю. В каждом случае надо спрашивать, сколько всего долей в целом. Например, сколько четвертых долей круга в целом круге? Сколько третьих долей отрезка во всем отрезке? и т. п. Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. В этом их основное назначение. Поэтому решение задач на нахождение доли числа и числа по его доле выполняется на наглядной основе.
Рассмотрим, как можно ознакомить учащихся с решением задач каждого вида. Сначала вводятся задачи на нахождение доли числа. Для ознакомления с решенном задач лучше предлагать задачи, которые легко иллюстрировать. Например, предлагается задача: «От полоски длиной 15 см отрезали —1/3 ее. Чему равна длина отрезанного куска полоски?» Ученики вырезают полоску длиной 15 см. Затем выясняется, как найти одну третью часть полоски (разделить ее на 3 равные части и взять одну такую часть). Учащиеся практически выполняют деление (перегибают полоску), а затем отрезают одну третью часть. Запись решения выполняется так: 15:3 = 5 (см) –длина отрезанного куска. Ответ: 5 см. При решении других задач достаточно воспользоваться чертежом: число изобразить отрезком, который учащиеся делят на заданное число равных частей, обозначают долю, после чего выполняют решение устно или письменно. В дальнейшем задачи на нахождение доли числа должны включаться для устной и письменной работы. Следует больше включать заданий вида: сколько сантиметров в Надо объяснить детям, почему принято говорить: «половина второго», «без четверти 10» и т. п. Задачи на нахождение числа по его доле вначале надо брать такие, чтобы их можно было непосредственно иллюстрировать, например: «Серёжа отрезал от куска проволоки 4 см. Это Изобразим кусок проволоки, который отрезал Сережа. (Чертят отрезок длиной 4 см.) Какую часть всего куска составляет отрезанный кусок (одну третью часть). Как изобразить весь кусок? (Взять 3 раза по 4 см.) Почему? (4 см — это Запись решения: 4· 3 = 12(см) –длина всего куска проволоки. Ответ: 12 см. Далее оба вида задач предлагаются в перемежении и предлагаются как для устного решения, так и для письменного решения. 4.2. Углубление знаний о долях (М.4, часть 2, с. 103-104). Образование дробей, как и образование долей рассматривается с помощью наглядных пособий ( термин «дробь» по традиционной программе не используется, что весьма непонятно). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


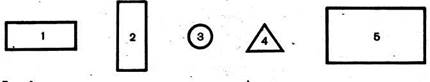





 . Число 2 показывает, что круг, квадрат или другая фигура (или предмет) разделены на две равные части, а число 1 показывает, что взяли одну такую часть.
. Число 2 показывает, что круг, квадрат или другая фигура (или предмет) разделены на две равные части, а число 1 показывает, что взяли одну такую часть.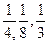 и др. и объясняют, что показывает в этой записи каждое число.
и др. и объясняют, что показывает в этой записи каждое число.  отрезка (прямоугольника, бумажной полоски и т.п.) надо данный отрезок (прямоугольник, полоску и т.п.) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке (прямоугольнике, полоске и т.п.) 5 пятых долей, что одна пятая доля записывается так:
отрезка (прямоугольника, бумажной полоски и т.п.) надо данный отрезок (прямоугольник, полоску и т.п.) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке (прямоугольнике, полоске и т.п.) 5 пятых долей, что одна пятая доля записывается так: 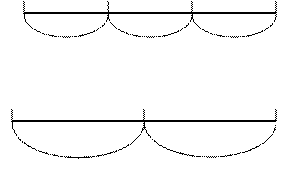
 м? Сколько минут в
м? Сколько минут в  часа и т. д.?
часа и т. д.?