
|
|
Последовательного исключения неизвестных12 (методом Гаусса). Контрольные вопросы: 1. Система m линейных уравнений с n неизвестными. 2. Основная матрица системы линейных уравнений. 3. Расширенная матрица системы линейных уравнений. 4. Решение системы линейных уравнений. 5. Совместная система линейных уравнений. 6. Несовместная система линейных уравнений. 7. Определенная система линейных уравнений. 8. Неопределенная система линейных уравнений. 9. Равносильные системы линейных уравнений. 10. Элементарные преобразования системы линейных уравнений. 11. Ранг матрицы. 12. Теорема Кронекера-Капелли. 13. Алгоритм решения системы линейных уравнений методом Гаусса. План занятия. 1. Теоретический диктант. 2. Решение типовых задач.
Задание 1.Решить систему линейных уравнений методом Гаусса: 1) 2) 3) 4) 5) 6)
7) 8)
Практическое занятие 8. Решение систем линейных уравнений Матричным методом. План занятия. 1. Самостоятельная работа. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. Решить систему линейных уравнений матричным методом: 1) 2) 3) 4) 5) 6) Практическое занятие 9. Решение систем линейных уравнений Методом Крамера.
Контрольные вопросы: 1. Теорема Крамера. План занятия. 1. Теоретический диктант. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. Решить систему линейных уравнений методом Крамера: 1) 2) 3) 4) 5) Практическое занятие 10. Векторы и операции над ними. Линейная комбинация системы векторов. Контрольные вопросы: 1. n-мерный вектор. 2. n-мерное векторное пространство. 3. Равные векторы. 4. Нулевой вектор. 5. Сумма векторов. 6. Произведение вектора на число. 7. Система векторов. 8. Линейная комбинация системы векторов. 9. Длина вектора. 10. Скалярное произведение векторов. 11. Ортогональные векторы. 12. Единичный (нормированный) вектор. План занятия. 1. Теоретический диктант. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1.Заданы векторы Задание 2.Заданы векторы Задание 3.Найдите длину вектора
Задание 4.Вычислите скалярное произведение векторов Задание 5.Найти скалярное произведение векторов
Задание 6.Найти квадрат длины вектора Задание 7.Найти |
Задание 8.Даны векторы a) b)
Практическое занятие 11. Система векторов и ее линейная зависимость. Базис системы векторов. Контрольные вопросы: 1. Линейно зависимая система векторов. 2. Линейно независимая система векторов. 3. Максимальная линейно независимая подсистема системы векторов. 4. Базис системы векторов. 5. Ранг системы векторов. План занятия. 1. Теоретический диктант. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. На основании определения установить, является ли данная система векторов линейно зависимой или линейно независимой: 1) 2) 3) 4) 5) 6)
Задание 2. Для данной системы векторов найти ранг, какой-нибудь базис и выразить через этот базис все векторы системы: 1) 2) 3) 4) 5) 6)
Практическое занятие 12. Базис и ранг системы векторов. Разложение вектора по базису.
Контрольные вопросы: 1. Максимальная линейно независимая подсистема системы векторов. 2. Базис системы векторов. 3. Ранг системы векторов. План занятия. 1. Самостоятельная работа. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. Относительно базиса а) доказать, что векторы б) найти координаты вектора 1) 2) 3) 4) 5)
Практическое занятие 13. Однородные системы линейных уравнений. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
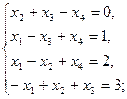
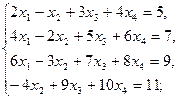
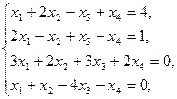
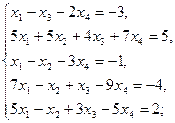
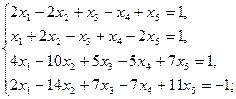

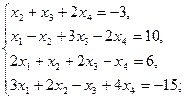
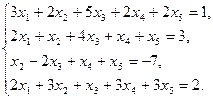





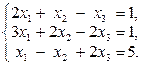
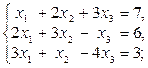
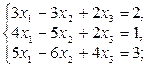
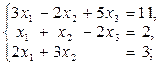
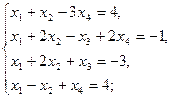
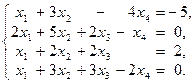
 ,
,  ,
,  относительно некоторого базиса. Найдите координаты вектора
относительно некоторого базиса. Найдите координаты вектора  относительно этого же базиса.
относительно этого же базиса. ,
,  , если
, если  ,
,  ,
,  .
.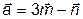 ,
,  , если
, если  ,
, 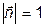 ,
,  .
. и
и  где
где  - единичные векторы, составляющие между собой попарно углы, равные
- единичные векторы, составляющие между собой попарно углы, равные  .
. , если
, если  .
. |, если
|, если  ,
,  ,
,  =3,
=3,  .
. ={6,-3,2}. Вычислить:
={6,-3,2}. Вычислить: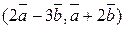
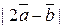 .
.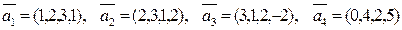 ;
; ;
; ;
;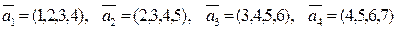 ;
; ;
; .
. ;
; ;
;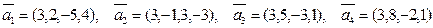 ;
; ;
;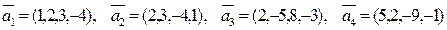 ;
; ,
, 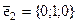 ,
,  заданы векторы
заданы векторы  .
.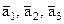 образуют базис пространства
образуют базис пространства  ;
; в базисе
в базисе 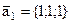 ,
, 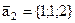 ,
, 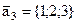 ,
,  ;
; ,
,  ,
, 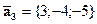 ,
,  ;
;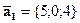 ,
, 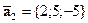 ,
, 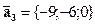 ,
, 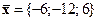 ;
; ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ,
,  .
.