
|
|
Решение систем линейных уравнений методом12 ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ для студентов 1 курса группы ЭОО 12 Практическое занятие 1. Матрицы и операции над ними. Контрольные вопросы: 1. Матрица размера 2. Квадратная матрица 3. Главная диагональ квадратной матрицы. 4. Побочная диагональ квадратной матрицы. 5. Нулевая матрица. 6. Единичная матрица. 7. Матрица ступенчатого вида. 8. Элементарные преобразования матриц. 9. Сумма матриц. 10. Произведение матрицы на число. 11. Транспонирование матрицы. 12. Произведение матриц.
План занятия. 1. Теоретический диктант. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1(устно). Чему равны в матрице A элементы Задание 2 (устно). Какие элементы в матрице Задание 3 (устно). Укажите, какие из матриц Задание 4 (устно). Даны две матрицы 1) A = B; 2) A > B; 3) Задание 5. Даны матрицы 1) матрицы 2) матрицы Задание 6.Найдите матрицу X, если: 1) 2) Задание 7. Перемножьте матрицы: 1) 2) 3) 4) 5)
Задание 8. Найти 1) 2) 3) 4) 5) Задание 9. Вычислить матричный многочлен: 1) 2) 3) 4) 5)
Практическое занятие 2. Определители. Вычисление определителей Го и 3-го порядков. Вычисление определителей порядка Контрольные вопросы: 1. Перестановка 2. Инверсия перестановки. 3. Четная перестановка. 4. Нечетная перестановка. 5. Определитель 6. Свойства определителей. 7. Вычисление определителя второго порядка. 8. Вычисление определителя третьего порядка (правило Сарриуса). 9. Алгебраическое дополнение элемента определителя. 10. Минор элемента. 11. Разложение определителя по 12. Разложение определителя по 13. Связь алгебраического дополнения и минора элемента. 14. Вычисление определителей порядка
План занятия. 1. Теоретический диктант. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1(устно). Как изменится определитель 3-го порядка, если у всех его элементов изменить знак на противоположный? Задание 2. Определить число инверсий в перестановке: 1) 2) 3) 4) Задание 3.Подберите 1) 2) 3) 4) Задание 4.Входит ли в определитель 1) 2) 3) 4) 5) 6) Задание 5.Вычислить определители: 1) 2) 3) 4) 5) 6) 7) 8) Задание 6. Найдите 1) 2) 3) Задание 7.Разложить следующие определители: 1) 2) 3)
Задание 8(устно). Как изменится определитель n-го порядка, если: 1) каждый его элемент умножить на -1; 2) его строки записать в обратном порядке; 3) к каждой строке, начиная со 2-ой, прибавить предыдущую. Задание 9. Вычислить определители: 1) 2) 3) 4) 5) 6)
Практическое занятие 3. Обратная матрица. Нахождение обратной матрицы С помощью линейных преобразований. Контрольные вопросы: 1. Обратимая матрица. План занятия. 1. Проверка домашнего задания. 2. Решение типовых задач.
Задание 1.Непосредственным подсчётом покажите, что Задание 2.При каких значениях параметра λ матрица имеет обратную? 1) 2)
Задание 3. Для матрицы 1) 2) 3) 4) 5) 6) Практическое занятие 4. Алгебраическое дополнение и минор элемента. Нахождение обратной матрицы с помощью Алгебраических дополнений. Контрольные вопросы: 1. Теорема о нахождении обратной матрицы с помощью алгебраических дополнений. План занятия. 1. Самостоятельная работа. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. Для матрицы
1) 2) 3) 4) 5) 6)
Практическое занятие 5. Матричные уравнения. План занятия. 1. Самостоятельная работа. 2. Проверка домашнего задания. 3. Решение типовых задач.
Задание 1. Решить матричное уравнение: 1) 2) 3) 4) 5) 6) 7) Практическое занятие 6. Рубежная аттестация 1. В-0
Практическое занятие 7. Решение систем линейных уравнений методом 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. -го порядка.
-го порядка. ,
,  , если
, если  ?
? составляют главную диагональ, а какие – побочную?
составляют главную диагональ, а какие – побочную? ,
,  ,
,  ,
,  ,
,  ,
,  являются диагональными, треугольными, ступенчатыми?
являются диагональными, треугольными, ступенчатыми? и
и  . Какое из соотношений верно?
. Какое из соотношений верно? ; 4) A = B = E;
; 4) A = B = E;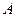 и
и  . Найти:
. Найти: и
и  , если
, если  ,
,  ;
; и
и  ,
,  .
. ;
; .
.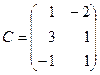 ,
,  ;
; ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  .
. , если:
, если: ,
,  ;
; ,
,  ;
;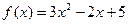 ,
,  ;
; ,
,  ;
; ,
,  .
. , если
, если  ,
,  ,
,  ;
; , если
, если  ,
,  ,
,  ,
,  ;
; , если
, если  ,
,  ,
,  ;
; , если
, если  ,
,  ,
,  ;
; , если
, если  ,
,  ,
,  .
.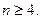
 -ой строке.
-ой строке. -му столбцу.
-му столбцу. ;
; ;
; ;
; .
. и
и  так, чтобы перестановка
так, чтобы перестановка была нечетной;
была нечетной; была четной;
была четной; была четной;
была четной; была нечетной.
была нечетной. ,
,  ;
; ,
,  ,
,  ;
;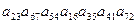 ,
,  ,
,  ,
,  ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. из уравнения:
из уравнения: ;
; ;
; .
. по элементам 4-го столбца;
по элементам 4-го столбца; по элементам 1-го столбца;
по элементам 1-го столбца; по элементам 3-ей строки.
по элементам 3-ей строки. ;
; ;
; ;
; ;
; ;
; .
. , если
, если  ,
,  . Будет ли матрица B обратной A?
. Будет ли матрица B обратной A? ;
; .
. ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
;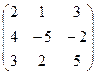 ;
; ;
; .
. ;
; ;
; ;
; ;
;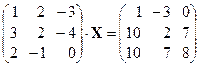 ;
; ;
; .
.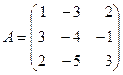 и
и  . Найти:
. Найти:  ;
; ;
; . Сделать проверку.
. Сделать проверку. ,
,  .
. ;
; .
. ;
; .
.