
|
|
Однородные линейные системыОбщее решение однородной системы Однородной линейной системой называется система уравнений вида
Любая однородная система совместна, так как всегда имеет нулевое (тривиальное) решение. Для существования нетривиального решения необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных. Особенностью однородной системы является то, что всякая линейная комбинация ее решений вновь является решением системы. Определение. Если ранг матрицы равен Для отыскания общего решения системы достаточно найти ее фундаментальную систему решений
Фундаментальная система решений строится следующим образом. Выделяем базисную систему уравнений, главные и свободные неизвестные. Предположим, что свободными являются неизвестные
Принимая значения элементов
Пример. Найти фундаментальную систему решений и построить общее решение системы уравнений
Приведем матрицу системы к ступенчатому виду
Очевидно, ранг матрицы системы равен 3, следовательно, фундаментальная система будет состоять из двух решений. За главные неизвестные можно принять
Задаем свободные неизвестные
Решая базисную систему, получим фундаментальные решения
Тогда общее решение
Задачи Найти фундаментальную систему решений и построить общее решение систем уравнений. 1. 3. 5. Неоднородные системы Общее решение неоднородной системы Рассмотрим неоднородную линейную систему Решения неоднородной и приведенной систем связаны следующим образом. Сумма любого решения неоднородной системы и любого решения приведенной системы является решением неоднородной системы. Разность двух произвольных решений неоднородной системы есть решение приведенной системы. Поэтому общее решение неоднородной системы можно получить, прибавляя к любому ее частному решению общее решение приведенной системы
Пример 1. Найти общее решение системы уравнений
Выделим базисную систему уравнений, приведя расширенную матрицу системы к ступенчатому виду
Так как
Найдем теперь частное решение неоднородной системы. Примем
Соответствующая приведенная система имеет вид
Для нахождения фундаментальной системы решений зададим значения свободных неизвестных
Тогда фундаментальные решения приведенной системы
Откуда общее решение неоднородной системы
Пример 2. Исследовать систему и найти общее решение в зависимости от значения параметра
Исследование начинаем с проверки системы на совместность. Так как система является квадратной, то по теореме Крамера при
Если
Пусть
Очевидно, что
Решая эту систему так же как в примере 1, получим общее решение
где Пусть
По виду первой строки ступенчатой матрицы определяем, что система несовместна. Задачи Исследовать системы уравнений и найти общее решение в зависимости от значений входящих в коэффициенты параметров: 1. 3. 5. 7. 9. Система
имеет единственное решение. Доказать, что Литература 1. Воеводин В. В. Линейная алгебра. — М.: «Наука», 1974. — 400 с. 2. Ефимов Н. В., Розендрон Э. Р. Линейная алгебра и многомерная геометрия. — М.: «Наука», 1974. — 250 с. 3. Проскуряков И. В. Сборник задач по линейной алгебре. — М.: «Наука», 1970. — 355 с. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
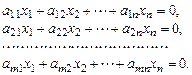
 , то всякая совокупность из
, то всякая совокупность из 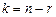 линейно независимых решений называется фундаментальной системой решений.
линейно независимых решений называется фундаментальной системой решений.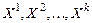 и составить их линейную комбинацию
и составить их линейную комбинацию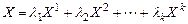 .
.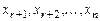 . Зададим определитель
. Зададим определитель  порядка
порядка 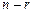 , отличный от нуля
, отличный от нуля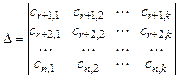 .
. го столбца определителя
го столбца определителя  .
.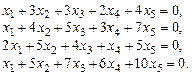
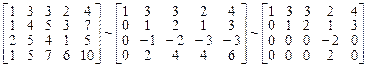 .
. , за свободные
, за свободные 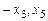 . Базисная система уравнений
. Базисная система уравнений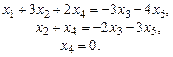
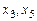
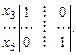
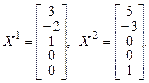
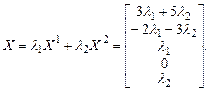
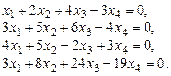 2.
2. 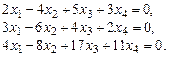
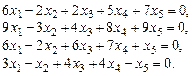 4.
4. 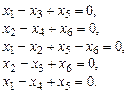
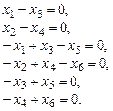
 . Соответствующая ей однородная система
. Соответствующая ей однородная система 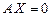 называется приведенной системой уравнений.
называется приведенной системой уравнений.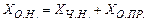 .
.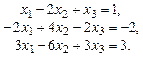
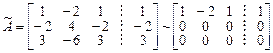 .
.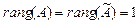 , то система совместна. Базисная система уравнений
, то система совместна. Базисная система уравнений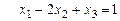 .
.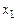 за главное, а
за главное, а 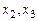 за свободные неизвестные. Положим
за свободные неизвестные. Положим 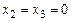 . Тогда частное решение
. Тогда частное решение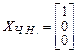 .
.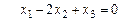 .
.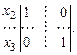
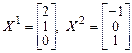 .
.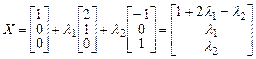 .
.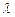 :
: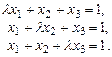
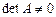 она совместна и имеет единственное решение. Для значений
она совместна и имеет единственное решение. Для значений 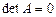 необходимы дополнительные исследования. Вычислим
необходимы дополнительные исследования. Вычислим 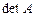
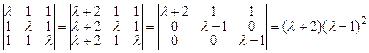 .
.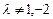 , то
, то 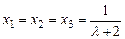 .
.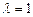 . Тогда расширенная матрица системы
. Тогда расширенная матрица системы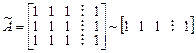 .
. .
. ,
,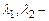 произвольные постоянные.
произвольные постоянные.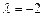 . Преобразуем расширенную матрицу системы к ступенчатому виду
. Преобразуем расширенную матрицу системы к ступенчатому виду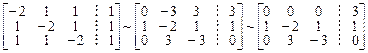 .
.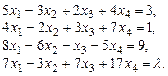 2.
2. 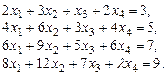
 4.
4. 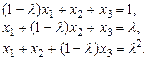
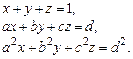 6.
6. 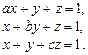
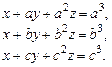 8.
8. 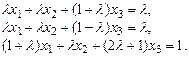
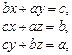
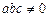 b и найти решение системы.
b и найти решение системы.