
|
|
Условие принадлежности двух прямых одной плоскости12 Примеры 1. Найти плоскость, проходящую через точку Для данной плоскости вектор нормали
2. Составить уравнение плоскости, проходящей через точки Воспользуемся уравнением
3. Составить уравнение плоскости, проходящей через точку Данная прямая проходит через точку 4. Найти уравнение плоскости, проходящей через точку Векторы нормали заданных плоскостей соответственно равны
5. Найти угол между плоскостями Векторы нормали заданных плоскостей соответственно равны 6. Доказать, что прямые Используем условие принадлежности двух прямых плоскости 7. Найти точку пересечения прямой Запишем параметрическое уравнение прямой Подставим полученные
8. Найти уравнение плоскости, проходящей через точку Из условия направляющий вектор прямой
9. Найти уравнение прямой, проходящей через точку Из условия вектор нормали плоскости 10. Найти точку, симметричную точке Эта задача решается в три этапа: Напишем уравнение прямой, проходящей через точку Находим точку пересечения прямой и плоскости Теперь решаем задачу о нахождении координат точки симметричной данной плоскости - прямой. Координаты этой точки, которую обозначим 11. Найти расстояние от точки Эта задача решается в три этапа: Напишем уравнение плоскости, проходящей через точку перпендикулярно прямой Вычислим проекцию точки на плоскость, для чего найдем пересечение прямой и плоскости И наконец находим расстояние от точки до прямой Кривые второго порядка Эллипс Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых до двух точек
Рис. 5 Каноническое уравнение эллипса
Параметры Эксцентриситет эллипса есть отношение Расстояния точки эллипса Примеры 1. Дано каноническое уравнение эллипса Из уравнения 2. Написать каноническое уравнение эллипса, зная, что расстояние между фокусами равно 8, а малая полуось равна 3. Из условия имеем Следовательно, каноническое уравнение эллипса имеет вид 3. Написать каноническое уравнение эллипса, зная, что большая полуось равна 6, а эксцентриситет равен 0,5. И условия Следовательно, каноническое уравнение эллипса имеет вид Гипербола Гиперболой называется геометрическое место точек, разность расстояний каждой из которых до двух точек
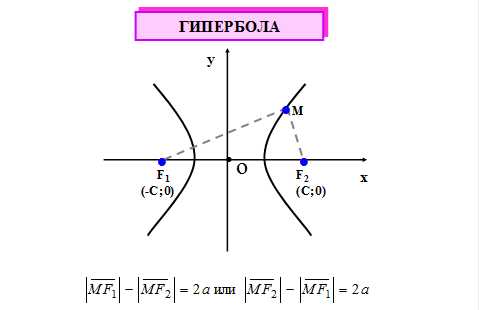
Рис. 6 Каноническое уравнение гиперболы Параметр Эксцентриситет гиперболы есть отношение Расстояния точки Прямые Гиперболы Примеры 1. Дана гипербола Из условия 2. Написать каноническое уравнение гиперболы, зная, что расстояние между фокусами Из условия 3. Написать каноническое уравнение гиперболы, зная, что вещественная полуось Используя формулу Парабола Параболой называется геометрическое место точек , одинаково удаленных от данной точки – фокуса и данной прямой – директрисы (рис. 7). Каноническое уравнение параболы имеет два вида: 1.
Рис. 7 2. Парабола Парабола Примеры 1. Составить геометрическое место точек, одинаково удаленных от точки Из условия 2. Написать уравнение параболы, проходящей через точку Каноническое уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. , параллельно плоскости
, параллельно плоскости  .
. . Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости:
. Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости: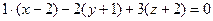 , отсюда
, отсюда  .
.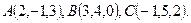
 , получим определитель
, получим определитель , затем – общее уравнение плоскости
, затем – общее уравнение плоскости 
 и прямую
и прямую  .
. с направляющим вектором
с направляющим вектором 
 . Составим вектор
. Составим вектор  . Вектор нормали
. Вектор нормали  искомой плоскости должен быть перпендикулярен векторам
искомой плоскости должен быть перпендикулярен векторам 
 . Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим
. Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим  , отсюда получаем общее уравнение плоскости
, отсюда получаем общее уравнение плоскости  .
. перпендикулярно плоскостям
перпендикулярно плоскостям  .
. . Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.
. Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.

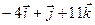 . Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим
. Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим  ,
,  отсюда получаем общее уравнение плоскости
отсюда получаем общее уравнение плоскости 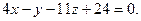
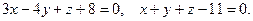
 . Тогда используя формулу
. Тогда используя формулу  , получим
, получим  , т.е. плоскости перпендикулярны.
, т.е. плоскости перпендикулярны. ,
,  пересекаются.
пересекаются. 0. Следовательно, эти прямые пересекаются.
0. Следовательно, эти прямые пересекаются. с плоскостью
с плоскостью 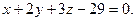
 .
. в уравнение плоскости , получим
в уравнение плоскости , получим , тогда
, тогда 
 . Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости
. Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости  .
. перпендикулярно прямой
перпендикулярно прямой  .
. будет вектором нормали для искомой плоскости, т.е.
будет вектором нормали для искомой плоскости, т.е.  . Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали
. Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали . Отсюда получим общее уравнение плоскости
. Отсюда получим общее уравнение плоскости  .
. .
. будет направляющим вектором для искомой прямой, т.е.
будет направляющим вектором для искомой прямой, т.е.  . Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой
. Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой 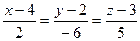 .
. относительно плоскости
относительно плоскости  .
. , это будет
, это будет  .
. . Это будет точка
. Это будет точка  .
. , вычисляются по формулам
, вычисляются по формулам  . Отсюда получим искомую точку
. Отсюда получим искомую точку 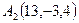 .
. до прямой
до прямой  .
.
 .
. .
. .
. и
и  , называемых фокусами, есть величина постоянная и равная
, называемых фокусами, есть величина постоянная и равная  (рис. 5).
(рис. 5).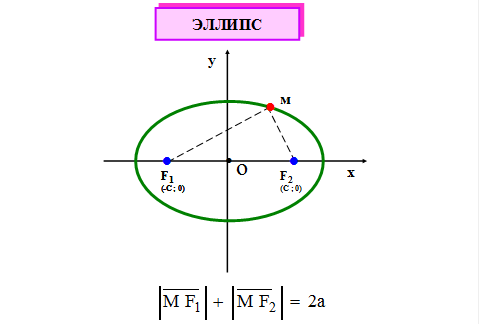
 .
. и
и  называются полуосями эллипса, большой и малой соответственно, если
называются полуосями эллипса, большой и малой соответственно, если 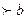 . Фокусы
. Фокусы  от центра.
от центра. .
. от его фокусов определяются формулами
от его фокусов определяются формулами  ,
,  .
. , найти его фокусы и эксцентриситет.
, найти его фокусы и эксцентриситет. и, следовательно, фокусы имеют следующие координаты
и, следовательно, фокусы имеют следующие координаты  , а эксцентриситет
, а эксцентриситет  .
. , а
, а  . Тогда
. Тогда  , отсюда
, отсюда  .
. .
. . Тогда
. Тогда  , отсюда
, отсюда  . Используя формулу
. Используя формулу  , найдем
, найдем 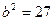 .
. .
.
 .
. ,
,  .
. называются асимптотами гиперболы.
называются асимптотами гиперболы. называются сопряженными.
называются сопряженными.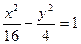 . Найти ее асимптоты, фокусы, эксцентриситет.
. Найти ее асимптоты, фокусы, эксцентриситет. , тогда получим уравнения асимптот
, тогда получим уравнения асимптот  . Найдем расстояние от центра до фокуса
. Найдем расстояние от центра до фокуса  , а затем напишем координаты фокусов
, а затем напишем координаты фокусов  и вычислим эксцентриситет
и вычислим эксцентриситет  .
. , а между вершинами
, а между вершинами 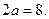
 , тогда из формулы
, тогда из формулы  получим
получим  , теперь можно написать каноническое уравнение гиперболы
, теперь можно написать каноническое уравнение гиперболы  .
. , а эксцентриситет
, а эксцентриситет  .
. , найдем
, найдем 
 , тогда из формулы
, тогда из формулы  , теперь можно написать каноническое уравнение гиперболы
, теперь можно написать каноническое уравнение гиперболы  .
. - парабола, симметричная относительно Ох;
- парабола, симметричная относительно Ох;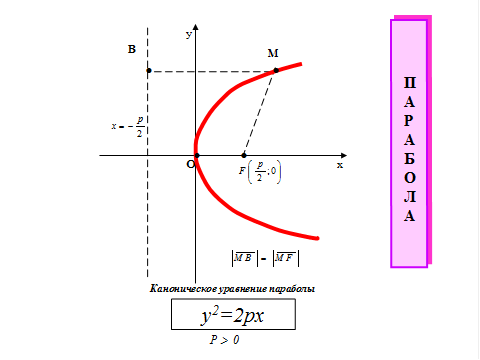
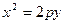 - парабола, симметричная относительно Oу.
- парабола, симметричная относительно Oу. имеет фокус
имеет фокус  и директрису
и директрису  .
. и директрису
и директрису  .
. и прямой
и прямой 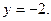
 , получаем
, получаем  , следовательно, это парабола, каноническое уравнение которой имеет вид
, следовательно, это парабола, каноническое уравнение которой имеет вид  или
или  .
. и
и  и симметричной относительно оси Ох.
и симметричной относительно оси Ох. , тогда искомое уравнение имеет вид
, тогда искомое уравнение имеет вид  .
.