Уравнение прямой в отрезках на осях
Прямая линия на плоскости
Уравнение прямой с угловым коэффициентом
 , , 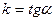 , где , где 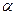 - угол наклона прямой к оси ОХ . - угол наклона прямой к оси ОХ .
Если 1)  , то прямая , то прямая 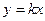 проходит через начало координат ; проходит через начало координат ;
2) 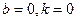 , то прямая , то прямая  совпадает с осью ОХ . совпадает с осью ОХ .
Замечание. Уравнение  описывает все прямые на плоскости за исключением прямых вида : описывает все прямые на плоскости за исключением прямых вида : 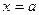 . .
Угол между двумя прямыми 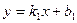 и и 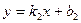 . .
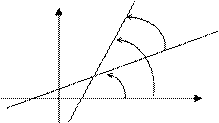  . Угол между прямыми . Угол между прямыми  (рис. 1). (рис. 1).
 , Y , Y 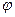
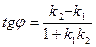 . . 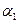  Х Х
Рис. 1
Из полученной формулы следует:
1. Условие параллельности двух прямых; 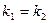 . .
2. Условие перпендикулярности двух прямых; 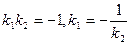 . .
Уравнение прямой, проходящей через заданную точку 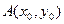 с заданным угловым коэффициентом с заданным угловым коэффициентом 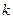
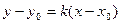 . .
Уравнение пучка прямых
Рассмотрим уравнение 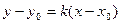 . .
Изменяя его угловой коэффициент, получим множество прямых, проходящих через точку 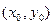 , которое назовем пучком прямых, а рассматриваемое уравнение – уравнением пучка прямых. , которое назовем пучком прямых, а рассматриваемое уравнение – уравнением пучка прямых.
Уравнение прямой , проходящей через две заданные точки
 
Уравнение прямой в отрезках на осях
 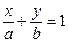 (рис. 2). (рис. 2).
Рис. 2
Примеры
1. Найти угол между двумя прямыми 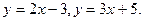
Из условия следует, что 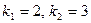 , тогда , тогда
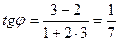 , , 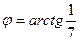 . .
2. Написать уравнение прямой, проходящей через точку А 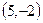
параллельно прямой 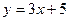 . .
Угловой коэффициент данной прямой 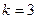 , а из условия параллельности угловой коэффициент искомой прямой , а из условия параллельности угловой коэффициент искомой прямой  .Следовательно, уравнение параллельной прямой имеет вид .Следовательно, уравнение параллельной прямой имеет вид 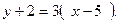 Отсюда Отсюда 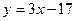 . .
3. Написать уравнение прямой, проходящей через точку А 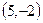
перпендикулярно прямой 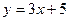 . .
Угловой коэффициент данной прямой 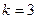  , а из условия перпендикулярности угловой коэффициент искомой прямой , а из условия перпендикулярности угловой коэффициент искомой прямой 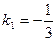 . .
Следовательно, уравнение перпендикулярной прямой имеет вид  
Отсюда  . .
4. Дана точка М( 1 ; 1 ). Провести через эту точку прямую под углом 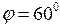 к прямой к прямой 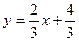 . .
Воспользуемся уравнением пучка прямых , проходящих через точку (1,1) ,
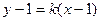 . Теперь найдем угловой коэффициент искомой прямой, воспользовавшись формулой : . Теперь найдем угловой коэффициент искомой прямой, воспользовавшись формулой :
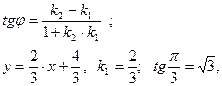
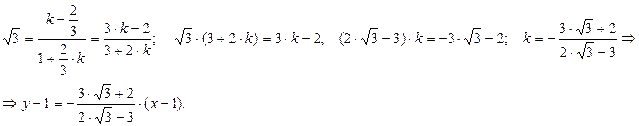
5.Дан треугольник с вершинами 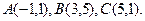 Найти уравнение высоты Найти уравнение высоты 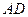 . .
Найдем уравнение стороны 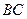 как уравнение прямой, проходящей через две заданные точки как уравнение прямой, проходящей через две заданные точки 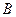 и и  . .
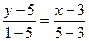 , отсюда , отсюда 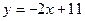 . .
Прямые 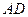 и и 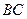 перпендикулярны, следовательно, угловой коэффициент прямой перпендикулярны, следовательно, угловой коэффициент прямой 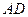 равен равен 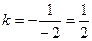 . .
Теперь запишем уравнение прямой 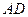 как уравнение прямой, проходящей через точку как уравнение прямой, проходящей через точку 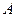 , с угловым коэффициентом , с угловым коэффициентом 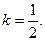
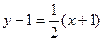 , отсюда , отсюда 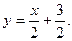
6. Дан треугольник с вершинами 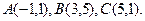 Найти уравнение медианы Найти уравнение медианы 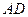 . .
Точка D лежит на середине отрезка ВС, тогда ее координаты равны полусумме, соответствующих координат, точек В и С, т.е.  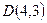 . .
Напишем уравнение прямой, проходящей через две точки A и B,
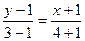 .Отсюда получаем искомое уравнение .Отсюда получаем искомое уравнение 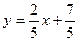 . .
7. Прямая отсекает на оси ОХ отрезок длинной 5, а на оси ОY отрезок длинной 4.
Найти уравнение этой прямой.
Используя уравнение в отрезках на осях , получим 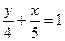 . Отсюда получаем . Отсюда получаем
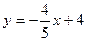 . .
Общее уравнение прямой
Всякое уравнение первого порядка вида 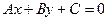
есть уравнение прямой, и, наоборот, любую прямую линию можно задать уравнением данного вида.
Уравнение 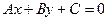 называется общим уравнением прямой. Если называется общим уравнением прямой. Если  , то из общего уравнения можно получить уравнение прямой с угловым коэффициентом , то из общего уравнения можно получить уравнение прямой с угловым коэффициентом 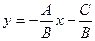 , т.е. , т.е.  . .
Пусть заданы две прямые  и и  . .
Угол 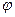 между этими прямыми можно определить из формулы : между этими прямыми можно определить из формулы :  . .
Отсюда следует , что равенство  будет условием параллельности, а равенство будет условием параллельности, а равенство  будет условием перпендикулярности двух прямых . будет условием перпендикулярности двух прямых .
Примеры
1. Определить точки пересечения прямой 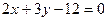 с координатными осями. с координатными осями.
Полагаем 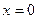 , подставляя в уравнение прямой, получаем , подставляя в уравнение прямой, получаем 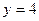 . .
Полагаем  , подставляя в уравнение прямой, получаем , подставляя в уравнение прямой, получаем 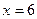 . .
Точка пересечения прямой с координатными осями имеет координаты 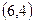 . .
2. Написать уравнение прямой, проходящей через точку  параллельно прямой параллельно прямой  . .
Перейдем от общего уравнения к уравнению прямой с угловым коэффициентом
 . Угловой коэффициент этой прямой . Угловой коэффициент этой прямой 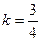 . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом, и получим . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом, и получим 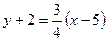 . Отсюда . Отсюда  . .
3. Написать уравнение прямой, проходящей через точку  перпендикулярно прямой перпендикулярно прямой 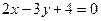 . .
Перейдем от общего уравнения к уравнению прямой с угловым коэффициентом
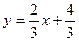 . Угловой коэффициент этой прямой . Угловой коэффициент этой прямой 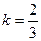 . Из условия перпендикулярности следует, что угловой коэффициент искомой прямой . Из условия перпендикулярности следует, что угловой коэффициент искомой прямой 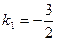 . .
Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом, и получим 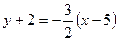 . Отсюда . Отсюда  . .
4. Найти угол между двумя прямыми 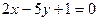 и и 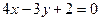 . .
Угол 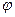 между этими прямыми можно определить из формулы : между этими прямыми можно определить из формулы :  . .
Здесь  , тогда , тогда  , отсюда , отсюда 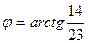 . .
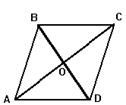 5. Дан ромб АВСD уравнения двух сторон ромба ВС и AD, а также диагонали BD (рис. 3). Найти уравнения диагонали АС. 5. Дан ромб АВСD уравнения двух сторон ромба ВС и AD, а также диагонали BD (рис. 3). Найти уравнения диагонали АС.
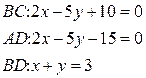
Найдем координаты точки В:
Рис. 3
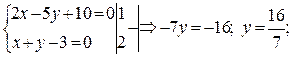 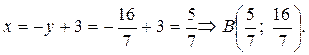
Найдем координаты точки D:
 ; ; 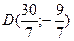 . .
Координаты центра - (B+D)/2: 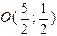 . .
Найдем уравнение диагонали АС:

6. Найти расстояние от точки 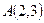 до прямой, проходящей через точки до прямой, проходящей через точки  и и 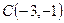 . .
Напишем уравнение прямой, проходящей через две заданные точки 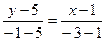 . Отсюда получаем . Отсюда получаем 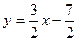 . Теперь напишем уравнение прямой, проходящей через точку . Теперь напишем уравнение прямой, проходящей через точку 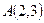 , перпендикулярно полученной прямой. Из условия перпендикулярности получим ее угловой коэффициент , перпендикулярно полученной прямой. Из условия перпендикулярности получим ее угловой коэффициент 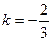 . Тогда уравнение перпендикуляра имеет вид . Тогда уравнение перпендикуляра имеет вид 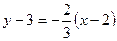 . Отсюда . Отсюда 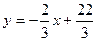 . Найдем проекцию точки . Найдем проекцию точки 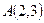 на прямую на прямую 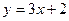 . Для чего решим систему уравнений . Для чего решим систему уравнений 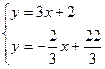 и получим и получим  , т.е. проекция точки , т.е. проекция точки 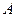 , которую обозначим , которую обозначим 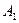 , имеет координаты , имеет координаты 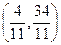 . Найдем расстояние . Найдем расстояние 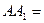  , что и будет искомым расстоянием. , что и будет искомым расстоянием.
7. Найти точку 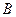 , симметричную точке , симметричную точке 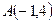 относительно прямой относительно прямой 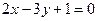 . .
Угловой коэффициент заданной прямой 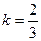 , тогда угловой коэффициент перпендикуляра к ней , тогда угловой коэффициент перпендикуляра к ней 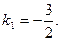 Теперь можно написать уравнение прямой, проходящей через точку Теперь можно написать уравнение прямой, проходящей через точку 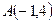 , перпендикулярно прямой , перпендикулярно прямой 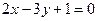 , , 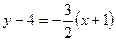 или или 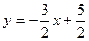 . Найдем проекцию точки . Найдем проекцию точки 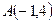 , которую обозначим , которую обозначим 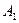 , на прямую , на прямую 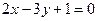 . Для чего решим систему уравнений . Для чего решим систему уравнений 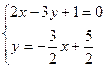 и получим координаты точки и получим координаты точки 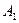 , , 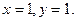
Обозначим 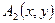 точку симметричную точке точку симметричную точке 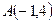 относительно прямой относительно прямой 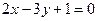 . Ее координаты найдем из соотношений . Ее координаты найдем из соотношений 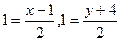 . Получим . Получим  , это и будут координаты симметричной точки. , это и будут координаты симметричной точки.
Прямая линия в пространстве 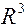
Дано (рис. 4). (рис. 4).
 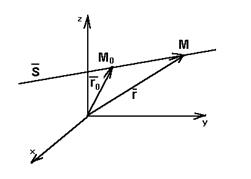
.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ,
, 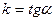 , где
, где 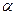 - угол наклона прямой к оси ОХ .
- угол наклона прямой к оси ОХ . , то прямая
, то прямая 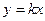 проходит через начало координат ;
проходит через начало координат ;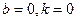 , то прямая
, то прямая  совпадает с осью ОХ .
совпадает с осью ОХ .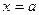 .
.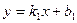 и
и 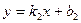 .
.
 . Угол между прямыми
. Угол между прямыми  (рис. 1).
(рис. 1). , Y
, Y 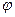
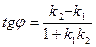 .
. 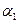
 Х
Х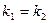 .
.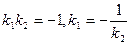 .
.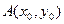 с заданным угловым коэффициентом
с заданным угловым коэффициентом 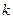
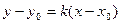 .
.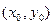 , которое назовем пучком прямых, а рассматриваемое уравнение – уравнением пучка прямых.
, которое назовем пучком прямых, а рассматриваемое уравнение – уравнением пучка прямых.


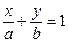 (рис. 2).
(рис. 2). 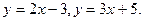
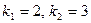 , тогда
, тогда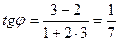 ,
, 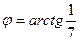 .
.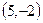
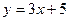 .
.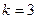 , а из условия параллельности угловой коэффициент искомой прямой
, а из условия параллельности угловой коэффициент искомой прямой  .Следовательно, уравнение параллельной прямой имеет вид
.Следовательно, уравнение параллельной прямой имеет вид 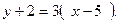 Отсюда
Отсюда 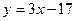 .
. , а из условия перпендикулярности угловой коэффициент искомой прямой
, а из условия перпендикулярности угловой коэффициент искомой прямой 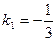 .
.
 .
.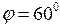 к прямой
к прямой 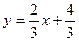 .
.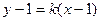 . Теперь найдем угловой коэффициент искомой прямой, воспользовавшись формулой :
. Теперь найдем угловой коэффициент искомой прямой, воспользовавшись формулой :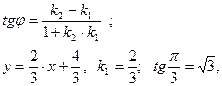
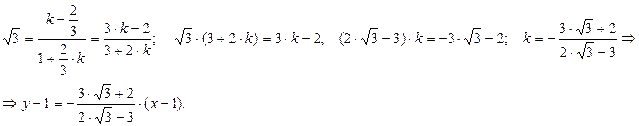
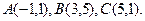 Найти уравнение высоты
Найти уравнение высоты 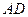 .
.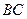 как уравнение прямой, проходящей через две заданные точки
как уравнение прямой, проходящей через две заданные точки 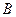 и
и  .
.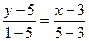 , отсюда
, отсюда 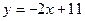 .
.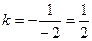 .
.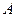 , с угловым коэффициентом
, с угловым коэффициентом 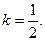
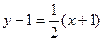 , отсюда
, отсюда 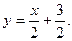
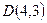 .
.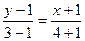 .Отсюда получаем искомое уравнение
.Отсюда получаем искомое уравнение 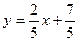 .
.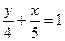 . Отсюда получаем
. Отсюда получаем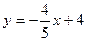 .
.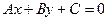
 , то из общего уравнения можно получить уравнение прямой с угловым коэффициентом
, то из общего уравнения можно получить уравнение прямой с угловым коэффициентом 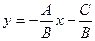 , т.е.
, т.е.  .
. и
и  .
. .
. будет условием параллельности, а равенство
будет условием параллельности, а равенство  будет условием перпендикулярности двух прямых .
будет условием перпендикулярности двух прямых .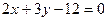 с координатными осями.
с координатными осями.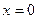 , подставляя в уравнение прямой, получаем
, подставляя в уравнение прямой, получаем 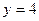 .
.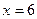 .
.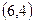 .
. параллельно прямой
параллельно прямой  .
. . Угловой коэффициент этой прямой
. Угловой коэффициент этой прямой 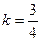 . Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом, и получим
. Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом, и получим 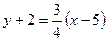 . Отсюда
. Отсюда  .
.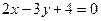 .
.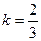 . Из условия перпендикулярности следует, что угловой коэффициент искомой прямой
. Из условия перпендикулярности следует, что угловой коэффициент искомой прямой 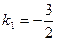 .
.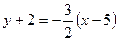 . Отсюда
. Отсюда  .
.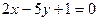 и
и 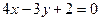 .
. , тогда
, тогда  , отсюда
, отсюда 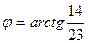 .
. 5. Дан ромб АВСD уравнения двух сторон ромба ВС и AD, а также диагонали BD (рис. 3). Найти уравнения диагонали АС.
5. Дан ромб АВСD уравнения двух сторон ромба ВС и AD, а также диагонали BD (рис. 3). Найти уравнения диагонали АС.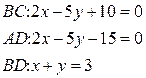
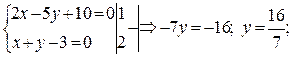
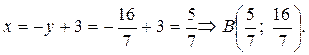
 ;
; 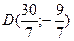 .
.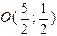 .
.
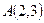 до прямой, проходящей через точки
до прямой, проходящей через точки  и
и 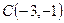 .
.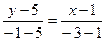 . Отсюда получаем
. Отсюда получаем 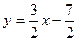 . Теперь напишем уравнение прямой, проходящей через точку
. Теперь напишем уравнение прямой, проходящей через точку 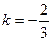 . Тогда уравнение перпендикуляра имеет вид
. Тогда уравнение перпендикуляра имеет вид 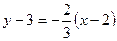 . Отсюда
. Отсюда 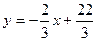 . Найдем проекцию точки
. Найдем проекцию точки 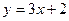 . Для чего решим систему уравнений
. Для чего решим систему уравнений 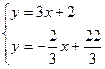 и получим
и получим  , т.е. проекция точки
, т.е. проекция точки 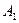 , имеет координаты
, имеет координаты 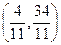 . Найдем расстояние
. Найдем расстояние 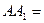
 , что и будет искомым расстоянием.
, что и будет искомым расстоянием.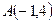 относительно прямой
относительно прямой 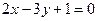 .
.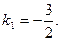 Теперь можно написать уравнение прямой, проходящей через точку
Теперь можно написать уравнение прямой, проходящей через точку 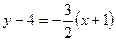 или
или 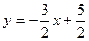 . Найдем проекцию точки
. Найдем проекцию точки 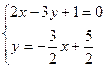 и получим координаты точки
и получим координаты точки 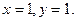
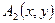 точку симметричную точке
точку симметричную точке 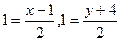 . Получим
. Получим  , это и будут координаты симметричной точки.
, это и будут координаты симметричной точки.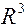
 (рис. 4).
(рис. 4).
