
|
|
Решения систем линейных уравнений методом Гаусса12
Следовательно, система имеет единственное решение. Найдем решение системы:
Пример 2
Следовательно, система имеет бесконечное множество решений, каждое из которых может быть найдено по формулам:
,
где численные значения z задаются произвольно. Пример 3
Следовательно, система несовместна. Векторная алгебра Основные понятия Вектором будем называть направленный отрезок
Векторы , параллельные одной прямой или лежащие на этой прямой , называются коллинеарными . Два вектора Векторы Произведением вектора Проекцией вектора
0
Проекция вектора на ось равна длине вектора, умноженной на косинус угла между положительным направлением оси и вектором, прl Если заданы точки
Теперь найдем разложение вектора Векторы
ij У Х Рис. 2 Выражение вида Скалярное произведение двух векторов Скалярное произведение векторов
Пусть даны два вектора Скалярное произведение двух векторов в этом случае вычисляется по формуле
Используя скалярное произведение, запишем формулы для вычисления проекции вектора
Нормой вектора Если вектор
Направляющие косинусы вектора Из определения скалярного произведения двух векторов имеем Пусть дан вектор
 Z Z
X
Тогда Пусть даны два вектора Вычислить 1. Скалярное произведение
2. Угол между векторами
3. Проекции векторов друг на друга
4. Направляющие косинусы вектора
5. Определить, при каком значении
6. Найти вектор Из условия коллинеарности 7. Даны векторы Вычислить скалярное произведение векторов
8. Найти норму вектора
Векторное произведение двух векторов Векторным произведением двух векторов а) б) перпендикулярен плоскости, образованной векторами
Замечание. Длина вектора Свойства векторного произведения 1. Векторное произведение равно нулю , если хотя бы один из векторов нулевой или векторы 2. 3. Векторное произведение ортов Исходя из определения векторного произведения, получим следующие равенства: Z
 (рис. 5). X (рис. 5). X 
Векторное произведение двух векторов , заданных своими координатами Пусть даны векторы Тогда их векторное произведение вычисляется по формуле
1. Найти векторное произведение двух векторов
2. Найти площадь треугольника Найдем векторы
3. Пусть даны векторы Найти длину их векторного произведения
4. Упростить выражение
5. Доказать тождество

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Пример 1
Пример 1
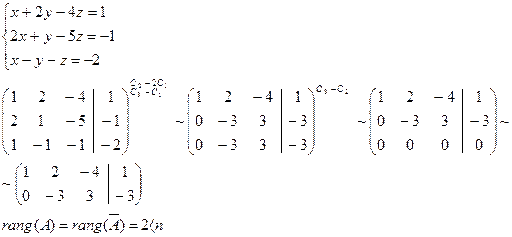
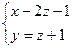
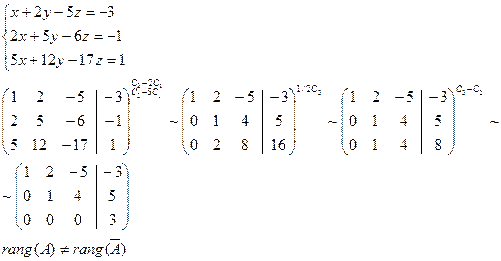
 , в котором
, в котором  - начало, а
- начало, а 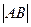 - длина вектора .
- длина вектора .
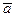 и
и 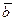 называются равными , если они имеют одно и то же направление , и
называются равными , если они имеют одно и то же направление , и  .
. называются компланарными, если они лежат в одной плоскости или параллельных плоскостях .
называются компланарными, если они лежат в одной плоскости или параллельных плоскостях . называется вектор, длина которого равна
называется вектор, длина которого равна  , коллинеарный вектору
, коллинеарный вектору  на ось
на ось  называется разность
называется разность  между координатами проекций конца и начала вектора
между координатами проекций конца и начала вектора 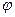

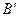

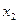
 .
. и
и  , то тогда вектор
, то тогда вектор .
. на составляющие, направленные по осям координат ,
на составляющие, направленные по осям координат , образуют базис в пространстве R3 и называются ортами (рис 2).
образуют базис в пространстве R3 и называются ортами (рис 2).
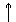








 Z
Z k
k  называется разложением вектора
называется разложением вектора  , где
, где  .
.
 .
.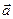 на вектор
на вектор  и наоборот,
и наоборот, ,
, 
 ,
,  .
. равна норме вектора .
равна норме вектора . , где
, где 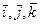 .
.
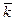
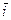
 Y
Y , где
, где  - углы, образованные вектором
- углы, образованные вектором  .
.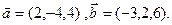
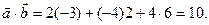
 ,
,  .
. ,
, 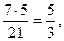
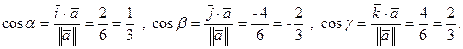
 векторы
векторы  будут ортогональны.
будут ортогональны.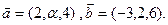
 , отсюда
, отсюда  .
. , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию 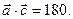
 , тогда
, тогда  , отсюда
, отсюда 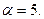
 и
и  , известно , что
, известно , что  и угол между векторами
и угол между векторами  и
и  равен
равен  .
.


 =
= 


 .
. .
. такой , что
такой , что
 , где
, где 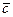 , можно наблюдать перемещение вектора
, можно наблюдать перемещение вектора 
 .
. .
.
 ,
, 
 ,
, 
 и
и 
 .
.
 .
.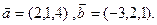
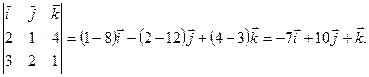
 , заданного координатами своих вершин,
, заданного координатами своих вершин, 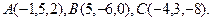
 и
и  .
.  .
. .
.  .
. и
и  и угол между векторами
и угол между векторами 


 .
.
 .
.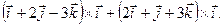
 =
=  =
=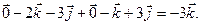

 =
=  =
=  =
=  +
+  .
.