
|
|
Линейное векторное пространство12 Решение систем уравнений методом Крамера 1. Определитель системы Вспомогательные определители
Решение системы
2. Определитель системы вычислим по формуле (4)
Вспомогательный определитель
определитель
определитель
Пусть дана линейная система
Таблица из числа Если Диагональ этой матрицы , составленная из элементов Квадратная матрица порядка Пусть дана матрица, А = Операции над матрицами Суммой А + В двух матриц А = ( Произведением kА матрицы А = ( В = ( Произведением матрицы А = ( Пусть дана квадратная матрица А = Если определитель квадратной матрицы равен нулю, то матрица называется вырожденной ( особенной ) , и невырожденной (неособенной) – в противоположном случае . Матрица В называется обратной для матрицы А, если АВ = ВА = Е и будем ее обозначать В = А-1 . Для невырожденной матрицы А существует обратная матрица, причем единственная и А-1 = Примеры 1. 2. 3. Дана матрица
Матричный способ решения систем линейных уравнений Пусть дана система n линейных уравнений с n неизвестными
А = Если определитель системы отличен от нуля , то ее решение находится следующим образом
Решить систему уравнений матричным способом 1. Cоставим матрицу системы
Найдем алгебраические дополнения
Получаем обратную матрицу
2. Составим матрицу системы
Найдем алгебраические дополнения
Получаем обратную матрицу Тогда Линейное векторное пространство Упорядоченная система из n чисел a = ( Векторы a = ( Суммой векторов a и b называется вектор Вектор 0 = (0,0,…,0) называется нулевым . Вектором, противоположным вектору a, назовем вектор -a =( Произведением вектора a на число k называется вектор ka = ( Вектор b называется линейной комбинацией векторов a1, a2, …, as, если существуют такие числа р1 , р2 , … , рs , что b = р1a1+ р2a2 + … + рsas . Система векторов a1 , a2 , … , as линейно зависима , если существуют такие числа р1 , р2 , … , рs , хотя бы одно из которых отлично от нуля , когда имеет место равенство р1a1+ р2a2 + … + рsas = 0 ,в противном случаи система линейно зависима. Система из n векторов образует базис линейного n - мерного пространства , если они линейно независимые и любой другой вектор линейного пространства является их линейной комбинацией . Система векторов e1=(1, 0, … , 0), e2=(0, 1, … , 0), … , en=(0, 0, …, 1), которые называются единичными, образует базис n - мерного векторного пространства . Доказать, что система векторов Рассмотрим равенство
то система имеет только нулевое решение и , следовательно , векторы
Теперь покажем, что любой вектор Действительно записанное ранее векторное равенство эквивалентно следующей линейной системе:
Теперь найдем координаты вектора Следовательно, в новом базисе вектор Пусть дана матрица А = Строки матрицы можно рассматривать как n - мерные векторы, которые могут быть линейно зависимые. Максимальное число линейно независимых строк матрицы А называется рангом этой матрицы. Пусть дана система линейных уравнений
Построим так называемую “расширенную” матрицу,
Система линейных уравнений тогда и только тогда совместна, когда ранг расширенной матрицы Совместная система тогда и только тогда обладает единственным решением, когда ранг матрицы А равен числу неизвестных. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
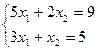
 .
. ,
,  .
.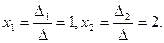
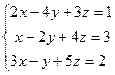
 = 2(-2)5+1(-1)3+3(-4)4 – ( 3(-2)3+2(-1)4+5(-4)1 ) =-25
= 2(-2)5+1(-1)3+3(-4)4 – ( 3(-2)3+2(-1)4+5(-4)1 ) =-25 вычислим разложением по элементам первой строки
вычислим разложением по элементам первой строки =
= 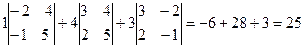 ,
, вычислим разложением по элементам первого столбца
вычислим разложением по элементам первого столбца ,
, вычислим разложением по элементам третьей строки
вычислим разложением по элементам третьей строки
 .
.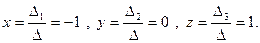
 .
. элементов
элементов  называется матрицей из
называется матрицей из  строк и
строк и  столбцов ;
столбцов ; называются элементами матрицы .
называются элементами матрицы . , то матрица называется квадратной порядка
, то матрица называется квадратной порядка  , называется главной диагональю .
, называется главной диагональю .
 называется транспонированной матрицей матрицы А .
называется транспонированной матрицей матрицы А . ) размерности
) размерности  ) такая , что
) такая , что  .
. k
k  ) размерности
) размерности  называется матрица С = АВ = (
называется матрица С = АВ = (  ) размерности
) размерности  такая , что
такая , что 
 .
.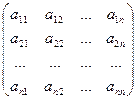 и ее определитель
и ее определитель  А
А 
 .
. .
. .
.
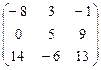
 =
=  , найти обратную.
, найти обратную.
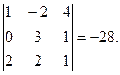

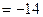 ,
, ,
,  ,
,  =
=  ,
, ,
,  ,
,  .
.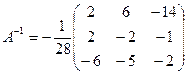 .
. .
. и Х =
и Х =  , тогда исходную систему можно записать в матричной форме АХ = в (*) .
, тогда исходную систему можно записать в матричной форме АХ = в (*) . .
. 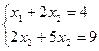
 и вычислим определитель матрицы
и вычислим определитель матрицы  .
.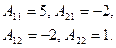
 , тогда
, тогда ,
, 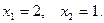
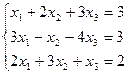
 и вычислим определитель матрицы
и вычислим определитель матрицы  .
.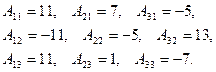
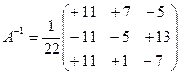 .
.

 ,
, 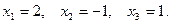
 ) называется n - мерным вектором, а числа
) называется n - мерным вектором, а числа  называются компонентами вектора a .
называются компонентами вектора a . ) будут считаться равными , если
) будут считаться равными , если  .
. a + b = (
a + b = (  ) .
) . ).
). ) .
) . образует базис в R3, и найти координаты вектора
образует базис в R3, и найти координаты вектора  в этом базисе .
в этом базисе . . Оно эквивалентно следующей линейной однородной системе :
. Оно эквивалентно следующей линейной однородной системе : , т.к. определитель системы
, т.к. определитель системы  ,
, - линейно независимые .
- линейно независимые . из R3 можно представить в виде их линейной комбинации, т.е.
из R3 можно представить в виде их линейной комбинации, т.е.  , и тем самым докажем , что векторы
, и тем самым докажем , что векторы  есть координаты вектора
есть координаты вектора  в новом базисе .
в новом базисе . . Так как определитель системы
. Так как определитель системы  , то, по правилу Крамера, система имеет решение при любой правой части, а это означает, что любой вектор из R3 можно выразить через векторы
, то, по правилу Крамера, система имеет решение при любой правой части, а это означает, что любой вектор из R3 можно выразить через векторы  в этом базисе, для чего запишем систему :
в этом базисе, для чего запишем систему : 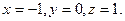
 .
. =
=  .
.