
|
|
Метод сопряженных градиентов
Метод сопряженных градиентов предназначен для решения систем линейных алгебраических уравнений с симметричной положительно определенной матрицей. Матрица Рассмотрим систему линейных алгебраических уравнений (4.1) с положительно определенной симметричной матрицей. Пусть
Так как матрица Будем искать этот минимум итерационным методом. Для этого предположим, что заданы два вектора
где
Параметры
Для определения минимума
Т.о., получаем систему уравнений
Так как
Это система двух уравнений с двумя неизвестными
Покажем, что метод сопряженных градиентов всегда сходится к решению системы
Так как векторы
где
Таким образом, последовательность Выберем начальные вектора
Для выполнения условия ортогональности векторов
Можно показать, что при таком выборе векторов Основной операцией метода сопряженных градиентов является вычисление произведений
Рассмотрим пример. Методом сопряженных градиентов решить систему линейных уравнений
Решение: Шаг 1. Возьмем произвольный вектор
Шаг 2.
Шаг 3.
ЛЕКЦИЯ № 13
4.6. Итерационные методы решения СЛАУ.
Метод простой итерации При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами. Изложим здесь один из этих методов — метод итерации. Пусть дана линейная система
Введя в рассмотрение матрицы
A =
систему (4.26) коротко можно записать в виде матричного уравнения Ах = b. Предполагая, что диагональные коэффициенты aii ≠ 0 ( i = 1, 2, .... n), разрешим первое уравнение системы (4.26) относительно х1, второе - относительно х2 и т. д. Тогда получим эквивалентную систему
x1 = β1 + α12 x2 + α13 x3 + …+ α1n xn ,
x2 = β2 + α21 x1 + α23 x3 + …+ α2n xn , (4.27) …………………………………….. xn = βn + αn1 x1 + αn2 x2 + …+ αn,n-1 xn-1 ,
где и αij = 0 при i = j ( i,j = 1, 2, .... n). Введя матрицы
а = систему (4.27) можем записать в матричной форме х = β+ α x(4.28) Систему (4.27) будем решать методом последовательных приближений. За нулевое приближение принимаем столбец свободных членов х (0) = β Далее, последовательно строим матрицы-столбцы
первое приближение - х(1) = β+ α x (0) второе приближение - х(2) = β+ α x (1) и т. д. Вообще говоря, любое (k+1)-е приближение вычисляют по формуле
х(k+1) = β+ α x (k) (k = 0, 1, 2, . . .). (4.29)
Если последовательность приближений x (0) ,x (1) , ....., x (k) , …. имеет предел x = lim x (k) при к → 0, то этот предел является решением системы (4.27). В самом деле, переходя к пределу в равенстве (4.29), будем иметь:
lim x (k+1) = β + lim x (k)
или х = β+ α x, т. е. предельный вектор хявляется решением системы (4.28), а следовательно, и системы (4.26). Заметим, что иногда выгоднее приводить систему (4.26) к виду (4.27) так, чтобы коэффициенты аи не были равны нулю. Метод последовательных приближений, определимых формулами (4.27) или (4.29), носит название метода итерации. Процесс итерации (4.29) хорошо сходится, т. е. число приближений, необходимых для получения корней системы (4.26) с заданной точностью, невелико, если элементы матрицы α малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (4.26) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют). Пример 1. Решить методом итерации систему
4x1 + 0,24 x2 - 0,08 x3 = 8, 0,09 x1 + 3 x2 - 0,15x з = 9, (4.30) 0,04 x1 - 0,08 x2 +4x3 = 20.
Решение. Здесь диагональные коэффициенты 4; 3; 4 системы значительно преобладают над остальными коэффициентами при неизвестных. Приведем эту систему к нормальному виду (4.27) x1 = 2 - 0,06x2 + 0,02x3, x2 = 3 - 0,03x1 + 0.05x3, (4.31) x3 = 5 - 0,01x1 + 0,02x2.. В матричной форме систему (4.31) можно записать так:
За нулевые приближения корней системы (4.30) принимаем: x1 (0)=2, x2 (0) =3, x3 (0)=5. Подставляя эти значения в правые части уравнений (4.31), получим лервые приближения корней:
x1 (1) = 2 - 0,06 · 3+ 0,02 · 5= 1,92; x2 (1) = 3 - 0,03 · 2 + 0,05 · 5 = 3,19; x3 (1) = 5 - 0,01 · 2 + 0,02 · 3 = 5,04.
Далее, подставляя эти найденные приближения в формулу (4.31) получим последующие приближения корней, табл. 20:
Таблица 20
Замечание. При применении метода итерации (формула (4.29) нет необходимости за нулевое приближение х(0) принимать столбец свободных членов, т.к. сходимость процесса итерации зависит только от свойств матрицы α, причем при выполнении известных условий, если этот процесс сходится при каком-нибудь выборе исходного начального приближения, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения. Поэтому начальный вектор х(0) в процессе итерации может быть взят произвольным.
Метод Зейделя Метод Зейделя представляет собой некоторую модификацию метода итерации. Основная его идея заключается в том, что при вычислении (к + 1)-гоприближения неизвестной xi учитываются уже вычисленные ранее (к + 1) - e приближения неизвестных x1, х2,…. Заметим, что указанная выше условие сходимости для простой итерации остается верной для итерации по методу Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации, но, вообще говоря, он приводит к более громоздким вычислениям. Процесс Зейделя может сходиться даже в том случае, если расходится процесс итерации. Однако это бывает не всегда. Возможны случаи, когда процесс Зейделя сходится медленнее процесса итерации. Более того, могут быть случаи, когда процесс итерации сходится, а процесс Зейделя расходится.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется положительно определенной, если скалярное произведение
называется положительно определенной, если скалярное произведение  для всех ненулевых векторов
для всех ненулевых векторов  . Для того чтобы матрица
. Для того чтобы матрица  - решение этой системы. Покажем, что в этом случае
- решение этой системы. Покажем, что в этом случае  . Имеем
. Имеем
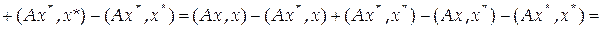
 .
. .
. и
и  . Последовательные приближения
. Последовательные приближения  к решению системы (4.1) будем строить по формулам
к решению системы (4.1) будем строить по формулам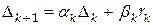 , (4.22)
, (4.22) , (4.23)
, (4.23) . (4.24)
. (4.24) и
и  будем определять из условия минимума функционала
будем определять из условия минимума функционала  и натянутой на векторы
и натянутой на векторы  и
и  , т.е. минимум функционала ищется на множестве
, т.е. минимум функционала ищется на множестве  . Преобразуем наш функционал на этом множестве
. Преобразуем наш функционал на этом множестве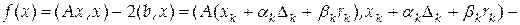
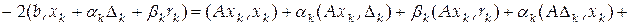
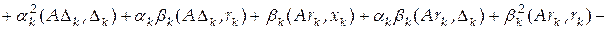
 .
.
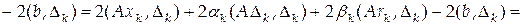
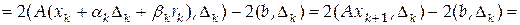
 ,
,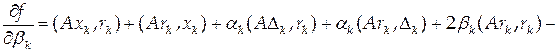

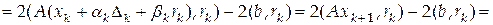
 .
. , (4.24)
, (4.24) . (4.25)
. (4.25)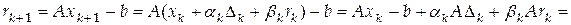
 , то последнюю систему можно представить в виде
, то последнюю систему можно представить в виде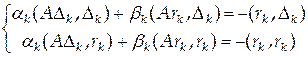
 ,
,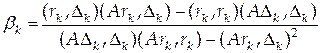
 и
и  , получим
, получим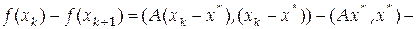

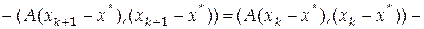
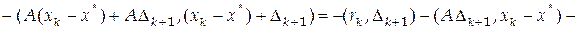
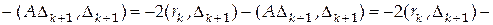
 .
.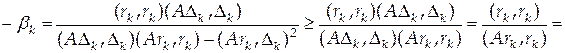
 ,
, - наибольшее собственное значение матрицы
- наибольшее собственное значение матрицы 
 .
. монотонно убывает и ограничена снизу значением
монотонно убывает и ограничена снизу значением  . Так как всякая монотонно убывающая последовательность сходится, т.е.
. Так как всякая монотонно убывающая последовательность сходится, т.е.  , то по признаку Коши имеем
, то по признаку Коши имеем  . Тогда из последнего неравенства следует, что
. Тогда из последнего неравенства следует, что  , а это означает, что последовательность векторов
, а это означает, что последовательность векторов  - произвольный вектор. Построим вектор
- произвольный вектор. Построим вектор  , где вектор
, где вектор  выбирается по направлению
выбирается по направлению  так, чтобы векторы
так, чтобы векторы  и
и  . Обозначим
. Обозначим  . Тогда
. Тогда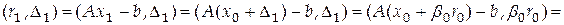
 .
. .
. -ом шаге, давая точное решение системы (4.1) (
-ом шаге, давая точное решение системы (4.1) (  и
и  , причем ни в какие другие операции матрица
, причем ни в какие другие операции матрица  .
. .Построим векторы
.Построим векторы  ,
, ,
, 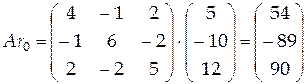 ,
,  ,
, ,
,  ,
, .
. ,
, ,
, ,
, ,
,  ,
,  ,
, ,
, ,
, ,
, ,
,  .
. ,
, ,
, ,
, ,
,  ,
,  ,
,  ,
, ,
, ,
, ,
, ,
,  .
. (4.26)
(4.26) x =
x =  , b=
, b=  ,
,
 при i ≠ j
при i ≠ j  иβ =
иβ =  ,
, =
=  +
+  ·
·