
|
|
Абсолютная величина и норма матрицыОсновные определения Система т п чисел (действительных или комплексных), расположенных в прямоугольной таблице из т строк и п столбцов,
называется матрицей. Строки и столбцы таблицы (3.1) называются рядами матрицы. Числа aij (i = 1, 2, .... т; j = 1, 2, . .., n), составляющие данную матрицу, называются ее элементами. Здесь первый индекс i обозначает номер строки элемента, а второй j — номер его столбца. Для матрицы (3.1) часто употребляется сокращенная запись
А = [ aij ] aij (i = 1, 2, .... т; j = 1, 2, . .., n)или А = [ aij ]m,n ,
причем говорят, что матрица А имеет тип m Если т = п, то матрица называется квадратной порядка п. Если же т ≠ п, то матрица называется прямоугольной. В частности, матрица типа 1
A =
называется диагональной и обозначается кратко так: [
Действия с матрицами 3.2.1. Сумма и разность матриц
Суммой (разностью) двух матриц А = [аij ]и B =[bij ]одинакового типа называется матрица С = [сi j]того же типа, элементы которой сi j= аij + bij или сi j= аij - bij соответственно. Из определения суммы матриц непосредственно вытекают следующие ее свойства: 1) А + (В + С) = (А + В) + С; 2) А + В = В + А ; 3) А + 0 = А .
Умножение матриц а)Умножение матрицы на число Произведением матрицы А = [аij ]на число α (или произведением числа αна матрицу А) называется матрица, элементы которой получены умножением всех элементов матрицы А на число α . Заметим, что если матрица А - квадратная порядка n, то det α A = α n det A.
б) Умножение матриц Пусть А = [аij ]и B =[bij ]матрицы типов соответственно m Изопределения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй и полученные произведения сложить. Произведение АВ имеет смысл тогда и только тогда, когда матрица А содержит в строках столько элементов, сколько элементов имеется в столбцах матрицы В. В частности, можно перемножать квадратные матрицы лишь одинакового порядка. Произведение двух матриц не обладает переместительным свойством, т. е., вообще говоря, АВ ≠ В А, в чем можно убедиться на примерах. Более того, может даже случиться, что произведение двух матриц, взятых в одном порядке, будет иметь смысл, а произведение тех же матриц, взятых в противоположном порядке, смысла иметь не будет. В тех частных случаях, когда АВ = В А, матрицы А и В называются перестановочными (коммутативными). Так, например, как нетрудно убедиться, единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем АЕ = ЕА = А.Таким образом, единичная матрица Е играет роль единицы при умножении. Если А и В — квадратные матрицы одного и того же порядка, то det (АВ) = det (ВА) = det A • det В. Эта формула вытекает из правила перемножения определителей.
в) Обратная матрица Определение 1. Обратной матрицей по отношению к данной называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Для матрицы Аобозначим обратную ей матрицу через А-1. Тогда по определению имеем: АА-1 = А-1 А = Е, где Е— единичная матрица. Нахождение обратной матрицы для данной называется обращением данной матрицы. Определение 2. Квадратная матрица называется неособенной, если определитель ее отличен от нуля. В противном случае матрица называется особенной, или сингулярной. Теорема. Всякая неособенная матрица имеет обратную матрицу.
Абсолютная величина и норма матрицы
Неравенство А ≤ В между матрицами А = [аij ]и B =[bij ]одинаковых типов обозначает, что аij ≤ bij . В этом смысле не всякие две матрицы сравнимы между собой. Под абсолютной величиной (модулем) матрицы А= [аij ]будем понимать матрицу | А| = [| аij| ] где | аij| — модули элементов матрицы А. Если А и В— матрицы, для которых операции А + В и АВ имеют смысл, то: а) | А + В | ≤ | А | + | В |; б) | А В | ≤ | А | · | В |; в) | α А | = | α | · | А |; | (α — число). Под нормой матрицы А = [аij ]понимается действительное число || A ||, удовлетворяющее условиям: а) ||A|| ≥ 0, причем ||A]| =0 тогда и только тогда, когда A = 0; б) || α А || = | α | · ||А ||( α — число) и, в частности, || - А || = ||А ||; в) || А + В || ≤ || А || + || В ||; г) || А В || ≤ || А || · || В ||; (А и В — матрицы, для которых соответствующие операции имеют смысл). В дальнейшем для матрицы А = [аij ]произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы; 1) || А || m = 2) || А || l = 3) || А || l =
ЛЕКЦИЯ № 7
4. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
4.1 Классификация методов решения систем линейных алгебраических уравнений
К решению систем линейных алгебраических уравнений сводится подавляющее большинство задач вычислительной математики. В настоящее время предложено огромное количество алгоритмов решения таких систем. Все методы решения линейных алгебраических уравнений можно разделить на две большие группы: прямые и итерационные. В прямых (или точных) методах решение системы находится за конечное число арифметических действий. Итерационные методы позволяют найти за конечное число итераций приближенное решение системы с любой наперед заданной точностью Примером прямого метода решения СЛАУ служит метод Крамера, в соответствии с которым
Однако на практике этот метод не используется, так как он требует выполнения очень большого количества арифметических операций. Большая часть существующих прямых методов укладывается в следующую схему. Пусть задана система
линейных алгебраических уравнений. Умножим обе части равенства (4.1) слева на такие матрицы
равносильна исходной и легко решается. Для этого достаточно, чтобы матрица
была треугольной или диагональной. Методы, основанные на подобных преобразованиях, составляют в настоящее время самую значительную группу среди численных методов задач алгебры. Одним из старейших является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. Он использует левые треугольные матрицы Непосредственно к методу Гаусса примыкают метод Жордана и метод оптимального исключения. Эти методы используют треугольные матрицы Перечисленные методы входят в группу методов исключения. Это название объясняется тем, что при каждом умножении на матрицу

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (3.1)
(3.1) n.
n. (3.2)
(3.2) ]. Если в (3.2) все αi = 1, то такая матрица называется единичной и обозначается буквой Е .
]. Если в (3.2) все αi = 1, то такая матрица называется единичной и обозначается буквой Е . n и р
n и р  | аij| (т-норма);
| аij| (т-норма);  | аij| (l-норма);
| аij| (l-норма); (k -норма).
(k -норма).  .
. ,
,  .
. (4.1)
(4.1) , при которых новая система
, при которых новая система (4.2)
(4.2)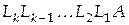
 и позволяет свести исходную систему уравнений к системе с правой треугольной матрицей. Этот метод легко реализуется на компьютере, его схема с выбором главного элемента позволяет решать системы с произвольной невырожденой матрицей, а компактная схема – получить результаты с повышенной точностью. Среди всех прямых методов метод Гаусса требует минимального объема вычислений.
и позволяет свести исходную систему уравнений к системе с правой треугольной матрицей. Этот метод легко реализуется на компьютере, его схема с выбором главного элемента позволяет решать системы с произвольной невырожденой матрицей, а компактная схема – получить результаты с повышенной точностью. Среди всех прямых методов метод Гаусса требует минимального объема вычислений. -ом шаге (
-ом шаге (