Свойства (умножения матриц).
1) Ассоциативность умножения матриц, т.е.,  справедливо справедливо  . .
2) Дистрибутивность сложения относительно умножения, т.е.,
 , ,  . .
 , ,  . .
3)  . .
5. Линейное пространство и его свойства, линейно зависимые и независимые вектора, их свойства. Базис и размерность линейного пространства.
Определение 1.Множество  вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы: , если удовлетворяются следующие аксиомы:
1)  является абелевой группой; является абелевой группой;
2) Для любых  и и  выполняются равенства: выполняются равенства:
а) Умножение  на на  не изменяет не изменяет  , т.е. , т.е.  . .
б)     . .
в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е.     . .
г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е.     . .
Обозначение.  . .
//НАПОМИНАНИЕ
Абелева (коммутативная) – значит «+» коммутативная операция. Группа:
1.1) + – ассоциативная операция.
1.2) В G  нейтральный элемент нейтральный элемент  . .
1.3)   симметричный элемент из симметричный элемент из  // //
Замечание.Так как  − абелева группа, то существует единственный нейтральный (нулевой) элемент, обозначаемый − абелева группа, то существует единственный нейтральный (нулевой) элемент, обозначаемый  , для каждого вектора , для каждого вектора  существует единственный симметричный (противоположенный) элемент, обозначаемый существует единственный симметричный (противоположенный) элемент, обозначаемый  , и для , и для  уравнение уравнение  имеет единственное решение имеет единственное решение  , называемое разностью , называемое разностью 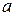 и и  . .
//НАПОМИНАНИЕ По свойству групп: Для  уравнения уравнения   имеют единственное решение: имеют единственное решение:  , ,  // //
Свойствалинейного пространства.
1)  выполняется выполняется  . .
2) 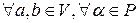 выполняется выполняется 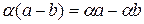 . .
3)  выполняется выполняется  . .
4)  выполняется выполняется  . .
5)  . .
6)  . .
7)  . .
Доказательство.
1) Так как    в силу г) в силу г)  имеем имеем 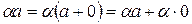   . Аналогично, . Аналогично,  имеем имеем      . .
2) В силу г) имеем   в силу разности векторов в силу разности векторов  . .
3) Следует из 2) при  . .
4) В силу в) имеем   в силу разности векторов в силу разности векторов 
5) Если  и и  , то умножая это равенство на симметричный элемент , то умножая это равенство на симметричный элемент  получаем: получаем:  и и    . Если . Если  и и  ,то ,то  . Т.о., если . Т.о., если  , то , то    . Обратное утверждение следует из 1). . Обратное утверждение следует из 1).
6) Из  . .
7) Аналогично. ■
Примеры.
1) Если  − поле и − поле и  , то , то  имеем имеем    − векторное пространство, называемое нулевым. − векторное пространство, называемое нулевым.
2)  − векторное пространство комплексных чисел над полем вещественных чисел. − векторное пространство комплексных чисел над полем вещественных чисел.  − векторное пространство вещественных чисел над полем рациональных чисел. − векторное пространство вещественных чисел над полем рациональных чисел.
3) Множество  матриц размера матриц размера  образует векторное пространство образует векторное пространство  . .
4) Множество многочленов степени не выше n образует векторное пространство  . .
5) Множество 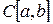 непрерывных на непрерывных на  функций образует векторное пространство функций образует векторное пространство  . .
6)  – n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: – n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел:  . Операции определены следующим образом: . Операции определены следующим образом:
 ; ;
 . .
2о. Линейно зависимые и линейно независимые системы векторов
Определение 2.Линейной комбинацией векторов  с коэффициентами с коэффициентами  называется выражение вида: называется выражение вида:  . .
Определение 3.Вектора  называются линейно независимыми, если называются линейно независимыми, если  , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими с этими  является нулевым вектором V, т.е. является нулевым вектором V, т.е.  . Вектора . Вектора  , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,  называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что 
Теорема 1.
1) Для того, чтобы элементы  были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных. были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.
2) Если среди  один элемент нулевой, то они линейно зависимы. один элемент нулевой, то они линейно зависимы.
3) Если часть элементов множества  линейно зависима, то и все элементы линейно зависимы. линейно зависима, то и все элементы линейно зависимы.
Доказательство.
1.   одновременно неравные нулю, так что одновременно неравные нулю, так что  Пусть например Пусть например  . .  - линейная комбинация остальных. - линейная комбинация остальных.

2. Если    и и  – любое, например, – любое, например,    линейно зависимы. линейно зависимы.
3. Если  – линейно зависимы, то – линейно зависимы, то  одновременно неравные нулю, так что одновременно неравные нулю, так что    и хотя бы одно из и хотя бы одно из  отлично от нуля отлично от нуля   линейно зависимы. ч.т.д. линейно зависимы. ч.т.д.
3о. Базис линейного пространства и координаты вектора в базисе.
Определение 5. Совокупность векторов  называют базисом в называют базисом в  , если , если
1. вектора  – линейно независимы; – линейно независимы;
2. для  может быть представлен как линейная комбинация этих векторов (т.е. найдутся может быть представлен как линейная комбинация этих векторов (т.е. найдутся   .) (1) .) (1)
При этом равенство (1) называется разложением элемента  по базису по базису  , а , а  называются координатами называются координатами  относительно базиса относительно базиса  . .
Теорема 2 (о единственности разложения по базису). Любой элемент  может быть единственным образом разложен по базису может быть единственным образом разложен по базису  , т.е. координаты вектора относительно базиса определяются однозначно. , т.е. координаты вектора относительно базиса определяются однозначно.
Доказательство.  Пусть Пусть  и и  . Тогда . Тогда  . В силу линейной независимости . В силу линейной независимости    , что и требовалось доказать. , что и требовалось доказать.
Теорема 3 (операции над векторами, заданными своими координатами). При сложении любых двух векторов  и и  их координаты (относительно любого фиксированного базиса в их координаты (относительно любого фиксированного базиса в  ) складываются; при умножении ) складываются; при умножении  на на  , все координаты вектора умножаются на это число. , все координаты вектора умножаются на это число.
Доказательство. Пусть  – базис в – базис в  , ,  , ,  . Тогда в силу аксиом линейного пространства . Тогда в силу аксиом линейного пространства  , ,  . В силу единственности разложения по базису . В силу единственности разложения по базису  что теорема доказана. что теорема доказана.
Примеры.
1. Базис в  – любое ненулевое число. – любое ненулевое число.
2.  . Базис образуют матрицы . Базис образуют матрицы  , ,  , …, , …,  с одним единичным элементом. с одним единичным элементом.
3.  – множество многочленов степени не выше n. Базис: – множество многочленов степени не выше n. Базис:  , ,  , …, , …,  . .
4.  – см. выше. – см. выше.
4о. Размерность линейного пространства.
Определение 6. Линейное пространство  называется n–мерным, если называется n–мерным, если
1. В нем  n линейно независимых векторов. n линейно независимых векторов.
2.  векторов линейно зависимы. векторов линейно зависимы.
Тогда n называется размерностью  и обозначается и обозначается  . .
Определение 7.Линейное пространство называется бесконечномерным, если в нем  любое число линейно независимых векторов. любое число линейно независимых векторов.
Выясним связь между понятием базиса и размерности линейного пространства.
Теорема 4. Если  – линейное пространство размерности n, то – линейное пространство размерности n, то  линейно независимых векторов этого пространства образуют его базис. линейно независимых векторов этого пространства образуют его базис.
Доказательство. Пусть  – система n линейно независимых векторов из – система n линейно независимых векторов из  . Если . Если  – любой вектор из – любой вектор из  , то по определению линейного пространства, вектора , то по определению линейного пространства, вектора  – линейно зависимы, т.е. – линейно зависимы, т.е. 

и среди  есть хотя бы одно отличное от нуля (из определения линейно зависимых векторов). Очевидно, что есть хотя бы одно отличное от нуля (из определения линейно зависимых векторов). Очевидно, что  (т. к. иначе (т. к. иначе  – линейно зависимы) – линейно зависимы) 
 , т.е. , т.е.
 – линейная комбинация – линейная комбинация   т. к. т. к.  – произвольный, то – произвольный, то  –базис. –базис.
Теорема 5. Если  имеет базис, состоящий из n элементов, то имеет базис, состоящий из n элементов, то  . .
Доказательство. Пусть  – базис в – базис в  . Достаточно показать, что . Достаточно показать, что  векторов векторов  линейно зависимы. Разложим их по базису: линейно зависимы. Разложим их по базису:
 , ,
…
 , ,
где  . .
Очевидно, что линейная зависимость векторов  эквивалентна линейной зависимости строк матрицы эквивалентна линейной зависимости строк матрицы
 . .
Ранг матрицы не более, чем n. Это значит, что базисный минор расположен не более чем в n строках. По теореме о базисном миноре оставшаяся строка представляет собой линейную комбинацию базисных строк. Значит, строки матрицы линейно зависимы, тогда вектора  линейно зависимы. линейно зависимы.
Примеры.
1.  . .
2.  . .
3.  . .
4.  . .
5.  . .
НАПОМИНАНИЕТеорема о базисном миноре.
Рассмотрим матрицу  , где , где  –поле матрицы размера –поле матрицы размера  . .
Определение 3.Число  называется рангом матрицы называется рангом матрицы  , если , если
1)  минор порядка минор порядка  , отличный от нуля. , отличный от нуля.
2) Все миноры  –го порядка равны нулю. –го порядка равны нулю.
Т.о., рангом матрицы называется порядок наибольшего отличного от нуля минора.
Минор  –го порядка, отличный от нуля, называется базисным минором, строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами. –го порядка, отличный от нуля, называется базисным минором, строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами.
Теорема 2(теорема о базисном миноре): Базисные строки (столбцы) линейно независимы. Любая строка (любой столбец) матрицы  является линейной комбинацией базисных строк (базисных столбцов). является линейной комбинацией базисных строк (базисных столбцов).
ВСЕ, ЧТО НИЖЕ, ПИСАТЬ НЕ НАДО!
5о. Изоморфизм линейных пространств.
Здесь будет показано, что линейные пространства одной и той же размерности в смысле некоторых свойств, связанных с введенными операциями, не отличаются друг от друга.
Определение 6.Два произвольных линейных пространства V и  над одним и тем же полем над одним и тем же полем  называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам называются изоморфными, если между элементами этих пространств можно установить взаимнооднозначное соответствие так, что если векторам  отвечают соответственные вектора отвечают соответственные вектора  , то вектору , то вектору 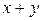 отвечает вектор отвечает вектор  , а вектору , а вектору  при при  отвечает вектор отвечает вектор  . .
6. Подпространство линейного пространства. Линейная оболочка векторов как пример подпространства. Размерность подпространства. Сумма и пересечение подпространств линейного пространства, их размерности. Прямая сумма подпространств.
1о. Определение подпространства и линейной оболочки
Определение 1.Непустое подмножество  линейного пространства линейного пространства  над полем над полем  называется линейным подпространством (или просто подпространством) линейного пространства называется линейным подпространством (или просто подпространством) линейного пространства  , если выполняются следующие свойства: , если выполняются следующие свойства:
1.  , их сумма , их сумма 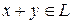 . .
2.  , ,  , имеем: , имеем:  . .
Лемма 1. Подпространство  векторного пространства векторного пространства  само является векторным пространством. само является векторным пространством.
Доказательство.
//Повторим определение векторного пространства:
Определение.Множество  вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы: , если удовлетворяются следующие аксиомы:
1)  является абелевой группой;// является абелевой группой;//
2) Для любых  и и  выполняются равенства: выполняются равенства:
а) Умножение  на на  не изменяет не изменяет  , т.е. , т.е.  . .
б)     . .
в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е.     . .
г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е.     . .
НАПОМИНАНИЕ
Абелева (коммутативная) – значит «+» коммутативная операция. Группа:
1.1) + – ассоциативная операция.
1.2) В G  нейтральный элемент нейтральный элемент  . .
1.3)   симметричный элемент из симметричный элемент из 
//
Покажем, что  – абелева группа относительно сложения. Так как ассоциативность и коммутативность выполняются для любых элементов – абелева группа относительно сложения. Так как ассоциативность и коммутативность выполняются для любых элементов  , то эти свойства выполняются и для , то эти свойства выполняются и для  . Осталось проверить, что . Осталось проверить, что  и и  , его противоположный элемент , его противоположный элемент  . Действительно, так как . Действительно, так как     при при   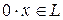   . Так . Так  , и , и  – элемент, противоположный – элемент, противоположный  , принадлежит , принадлежит    и и    и является противоположным к и является противоположным к  . Остальные свойства умножения на скаляр справедливы, так как они справедливы для любых элементов . Остальные свойства умножения на скаляр справедливы, так как они справедливы для любых элементов  , значит и для L. , значит и для L.
Примеры:
1)  и и  подпространства линейного пространства подпространства линейного пространства  . они называются несобственными подпространствами. . они называются несобственными подпространствами.
2)  – подпространство в пространстве – подпространство в пространстве  . .
3)  - многочлены степени не выше n. Подпространство: - многочлены степени не выше n. Подпространство:  - многочлены степени не выше k. - многочлены степени не выше k.
Рассмотрим множество  векторов пространства векторов пространства   . .
Определение 2.Линейной оболочкой множества  (линейной оболочкой (линейной оболочкой  ) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида ) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида
 , ,
где  – произвольные элементы – произвольные элементы  . .
Обозначение.  – линейная оболочка – линейная оболочка  . Множество . Множество  называется множеством или системой образующих для называется множеством или системой образующих для  . .
Лемма 2. Любая линейная оболочка является подпространством основного линейного пространства  , причем линейная оболочка является наименьшим подпространством, содержащим , причем линейная оболочка является наименьшим подпространством, содержащим  . .
Доказательство. То, что  – подпространство, следует из того, что для – подпространство, следует из того, что для  выполняются аксиомы 1о, 2о подпространства. Так как любое подпространство, содержащее вектора выполняются аксиомы 1о, 2о подпространства. Так как любое подпространство, содержащее вектора  содержит также их линейные комбинации, то это означает, что линейная оболочка содержит также их линейные комбинации, то это означает, что линейная оболочка  является подмножеством этого линейного подпространства. является подмножеством этого линейного подпространства.
Пример. Если рассмотреть 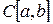 , и , и  , ,  , , 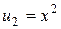 , …, , …, 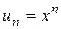 , то , то  . .
Лемма 3.
1. Если  – подпространство в – подпространство в   (размерность) (размерность) 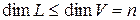 . .
2. Если подпространство  не совпадает со всем векторным пространством не совпадает со всем векторным пространством  размерности размерности  , то , то  . .
Доказательство. Методом от противного.
1. Если  и и    независимых векторов в независимых векторов в  по определению размерности пространства по определению размерности пространства  они линейно независимы в они линейно независимы в  , т.е. противоречие. , т.е. противоречие.
//НАПОМИНАНИЕ
Определение 6. Линейное пространство  называется n–мерным, если называется n–мерным, если
1. В нем  n линейно независимых векторов. n линейно независимых векторов.
2.  векторов линейно зависимы.// векторов линейно зависимы.//
2. Пусть   по теореме (Теорема: Если по теореме (Теорема: Если  – линейное пространство размерности n, то – линейное пространство размерности n, то  линейно независимых векторов этого пространства образуют его базис.) линейно независимых векторов этого пространства образуют его базис.)  любые любые  векторов образуют базис в векторов образуют базис в  . Но так как любые . Но так как любые  векторов образуют базис в векторов образуют базис в   значит любой элемент в значит любой элемент в  может быть представлен как их линейная комбинация и следовательно все элементы в может быть представлен как их линейная комбинация и следовательно все элементы в  представимы как линейная комбинация векторов из представимы как линейная комбинация векторов из   значит значит  и и  совпадают совпадают   . .
4о. Сумма и пересечение подпространств
Рассмотрим два подпространства  и и 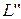 пространства пространства  . .
Определение 6.Будем называть суммой подпространств  и и 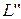 и обозначать и обозначать  множество всех векторов, которые можно представить в виде множество всех векторов, которые можно представить в виде  , где , где  и и  . .
Лемма 4.Сумма подпространств является подпространством.
Доказательство.Действительно, если есть  ; ;  , то , то  , ,  : :  , ,    . Также, . Также,  . ■ . ■
Если  , ,  , то , то  базис базис  , а в , а в 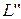 – базис – базис  . Каждый вектор из . Каждый вектор из  есть линейная комбинация есть линейная комбинация  , ,  , т.е. , т.е.  есть линейная комбинация этих векторов есть линейная комбинация этих векторов  , ,  . Выбрав из них линейно независимые, получаем базис в . Выбрав из них линейно независимые, получаем базис в  . .
Определение 7.Назовём пересечением подпространств  и и 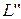 и обозначим и обозначим  множество векторов, которые принадлежат одновременно обоим подпространствам. множество векторов, которые принадлежат одновременно обоим подпространствам.
Лемма 5.Пересечение  есть подпространство. есть подпространство.
Доказательство.Если  , то , то  и и  и и 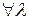 , ,  и и  и и   и и  . ■ . ■
Теорема 6.Сумма размерностей произвольных подпространств  и и 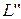 конечномерного линейного пространства конечномерного линейного пространства  равна сумме размерности пересения этх подпространств и размерности суммы этих подпространств, т.е. равна сумме размерности пересения этх подпространств и размерности суммы этих подпространств, т.е.  . .
Доказательство.Пусть  , ,  , ,  , ,  . Выберем в . Выберем в  базис базис  . Тогда по теореме (Теорема. Если элементы . Тогда по теореме (Теорема. Если элементы  составляют базис k-мерного подпространства составляют базис k-мерного подпространства  пространства пространства   , то этот базис может быть дополнен элементами , то этот базис может быть дополнен элементами  так, что совокупность так, что совокупность  , ,  – базис – базис  .) его можно дополнить до базиса .) его можно дополнить до базиса

| (1)
| подпространства  и до базиса и до базиса

| (2)
| подпространства  . Если . Если  , т.е. , т.е.  , то рассмотрим простое объединение базисов в , то рассмотрим простое объединение базисов в  и и  . .
Докажем в начале, что каждый вектор  является линейной комбинацией векторов является линейной комбинацией векторов
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 справедливо
справедливо  .
. ,
,  .
. ,
,  .
. .
. вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем
вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы:
, если удовлетворяются следующие аксиомы: является абелевой группой;
является абелевой группой; и
и  выполняются равенства:
выполняются равенства: на
на  не изменяет
не изменяет  , т.е.
, т.е.  .
.


 .
. .
.

 .
. .
. нейтральный элемент
нейтральный элемент  .
.
 //
// , для каждого вектора
, для каждого вектора  существует единственный симметричный (противоположенный) элемент, обозначаемый
существует единственный симметричный (противоположенный) элемент, обозначаемый  , и для
, и для  имеет единственное решение
имеет единственное решение  , называемое разностью
, называемое разностью 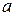 и
и  .
. уравнения
уравнения 
 имеют единственное решение:
имеют единственное решение:  ,
,  //
// выполняется
выполняется  .
.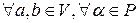 выполняется
выполняется 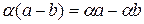 .
. выполняется
выполняется  .
. выполняется
выполняется  .
. .
. .
. .
.
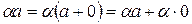
 . Аналогично,
. Аналогично, 

 .
.
 .
. .
.
 и
и  , то умножая это равенство на симметричный элемент
, то умножая это равенство на симметричный элемент  получаем:
получаем:  и
и 
 ,то
,то  . Т.о., если
. Т.о., если 

 .
. , то
, то 
 − векторное пространство комплексных чисел над полем вещественных чисел.
− векторное пространство комплексных чисел над полем вещественных чисел.  − векторное пространство вещественных чисел над полем рациональных чисел.
− векторное пространство вещественных чисел над полем рациональных чисел. матриц размера
матриц размера  образует векторное пространство
образует векторное пространство  .
. .
.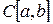 непрерывных на
непрерывных на  функций образует векторное пространство
функций образует векторное пространство  .
. – n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел:
– n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел:  . Операции определены следующим образом:
. Операции определены следующим образом: ;
; .
. с коэффициентами
с коэффициентами  называется выражение вида:
называется выражение вида:  .
. , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация
, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация  с этими
с этими  является нулевым вектором V, т.е.
является нулевым вектором V, т.е.  . Вектора
. Вектора 

 одновременно неравные нулю, так что
одновременно неравные нулю, так что  Пусть например
Пусть например  .
.  - линейная комбинация остальных.
- линейная комбинация остальных.

 и
и  – любое, например,
– любое, например, 
 одновременно неравные нулю, так что
одновременно неравные нулю, так что 
 и хотя бы одно из
и хотя бы одно из  отлично от нуля
отлично от нуля  называют базисом в
называют базисом в  – линейно независимы;
– линейно независимы; может быть представлен как линейная комбинация этих векторов (т.е. найдутся
может быть представлен как линейная комбинация этих векторов (т.е. найдутся 
 .) (1)
.) (1) по базису
по базису  называются координатами
называются координатами  относительно базиса
относительно базиса  Пусть
Пусть  и
и  . Тогда
. Тогда  . В силу линейной независимости
. В силу линейной независимости  , что и требовалось доказать.
, что и требовалось доказать. их координаты (относительно любого фиксированного базиса в
их координаты (относительно любого фиксированного базиса в  , все координаты вектора умножаются на это число.
, все координаты вектора умножаются на это число. . Тогда в силу аксиом линейного пространства
. Тогда в силу аксиом линейного пространства  ,
,  . В силу единственности разложения по базису
. В силу единственности разложения по базису  – любое ненулевое число.
– любое ненулевое число. . Базис образуют матрицы
. Базис образуют матрицы  ,
,  , …,
, …,  – множество многочленов степени не выше n. Базис:
– множество многочленов степени не выше n. Базис:  ,
,  .
. векторов линейно зависимы.
векторов линейно зависимы. .
. линейно независимых векторов этого пространства образуют его базис.
линейно независимых векторов этого пространства образуют его базис. – линейно зависимы, т.е.
– линейно зависимы, т.е. 

 есть хотя бы одно отличное от нуля (из определения линейно зависимых векторов). Очевидно, что
есть хотя бы одно отличное от нуля (из определения линейно зависимых векторов). Очевидно, что  (т. к. иначе
(т. к. иначе  , т.е.
, т.е. линейно зависимы. Разложим их по базису:
линейно зависимы. Разложим их по базису: ,
, ,
, .
. эквивалентна линейной зависимости строк матрицы
эквивалентна линейной зависимости строк матрицы .
. .
. .
. .
. .
. .
. , где
, где  .
. называется рангом матрицы
называется рангом матрицы  , если
, если , отличный от нуля.
, отличный от нуля. –го порядка равны нулю.
–го порядка равны нулю. над одним и тем же полем
над одним и тем же полем  отвечают соответственные вектора
отвечают соответственные вектора  , то вектору
, то вектору 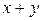 отвечает вектор
отвечает вектор  , а вектору
, а вектору  при
при  отвечает вектор
отвечает вектор  .
. линейного пространства
линейного пространства  , их сумма
, их сумма 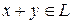 .
. ,
,  , имеем:
, имеем:  .
. и
и  , его противоположный элемент
, его противоположный элемент  . Действительно, так как
. Действительно, так как 


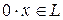
 , и
, и  – элемент, противоположный
– элемент, противоположный  и
и 
 и является противоположным к
и является противоположным к  и
и  подпространства линейного пространства
подпространства линейного пространства  – подпространство в пространстве
– подпространство в пространстве  .
. - многочлены степени не выше n. Подпространство:
- многочлены степени не выше n. Подпространство:  - многочлены степени не выше k.
- многочлены степени не выше k. векторов пространства
векторов пространства 
 .
. ) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида
) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида ,
, – произвольные элементы
– произвольные элементы  – линейная оболочка
– линейная оболочка  ,
,  ,
, 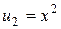 , …,
, …, 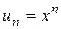 , то
, то  .
.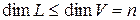 .
. , то
, то  .
. и
и 
 независимых векторов в
независимых векторов в 
 и
и 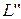 пространства
пространства  множество всех векторов, которые можно представить в виде
множество всех векторов, которые можно представить в виде  , где
, где  и
и  .
. , то
, то  ,
,  :
:  ,
, 

 . Также,
. Также,  . ■
. ■ ,
,  , то
, то  базис
базис  , а в
, а в  . Каждый вектор из
. Каждый вектор из  множество векторов, которые принадлежат одновременно обоим подпространствам.
множество векторов, которые принадлежат одновременно обоим подпространствам. , то
, то  и
и  и
и 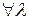 ,
,  и
и  и
и 
 и
и  . ■
. ■ .
. ,
,  ,
,  ,
,  . Выберем в
. Выберем в  . Тогда по теореме (Теорема. Если элементы
. Тогда по теореме (Теорема. Если элементы  составляют базис k-мерного подпространства
составляют базис k-мерного подпространства  , то этот базис может быть дополнен элементами
, то этот базис может быть дополнен элементами  так, что совокупность
так, что совокупность  – базис
– базис 

 . Если
. Если  , т.е.
, т.е.  , то рассмотрим простое объединение базисов в
, то рассмотрим простое объединение базисов в  является линейной комбинацией векторов
является линейной комбинацией векторов