
|
|
Свойства (сложения матриц).12 Примеры. 1. (R, +). Операция сложения коммутативна и ассоциативна. 2. (R, -). Операция вычитания не коммутативна и не ассоциативна. Например, 3. (R, 4. Умножение матриц является ассоциативной, но не коммутативной операцией. Определение 4. Элемент
Определение 5.Множество Определение 6. Элемент
Обычно умножение называют мультипликативной операцией, сложение – аддитивной. В случае мультипликативной операции результат операции
2°. Группа, свойства группы. Определение 7.Непустое множество G с заданной алгебраической операцией 1) 2) В G 3) Если Операция, относительно которой G − группа, называется групповой операцией. Если групповая операция Примеры. 1. (N,+) – коммутативная полугруппа без нейтрального элемента. 2. (N, 3. (Z, +)– аддитивная абелева (коммутативная) группа. 4. (Q, +)– аддитивная абелева (коммутативная) группа. 5. (R, +)– аддитивная абелева (коммутативная) группа. 6. (R, 7. (R 8. 9. Множество векторов на плоскости или в пространстве относительно операции сложения. Свойства группы. 1) В группе G Доказательство следует из теорем 1 и 2. Теорема 1. Нейтральный элемент единственен. Доказательство.
Одной паре соответствует 1 элемент Теорема 2. Если для Доказательство. Пусть для данного
2) Для
Доказательство. Покажем, что Предположи, что есть другое решение – z, то
3°. Кольцо, свойства кольца. В алгебре изучаются множества и с несколькими, например, с двумя, алгебраическими операциями. Определение 9. Непустое множество K с 2-мя операциями сложения и умножения называется кольцом и обозначается (K 1) (K, +) – абелева группа. 2) умножение на множестве K ассоциативно, т.е.
3) умножение дистрибутивно относительно сложения, т.е.
Кольцо называется коммутативным (понятия абелева кольца нет!!!), если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей. Примеры колец. 1. (Z; +; 2. Множество {0}, содержащее лишь одно число 0, образует кольцо, называемое нулевым кольцом. 3. Множество
образует коммутативное кольцо с единицей. 4. Множество V3 всех векторов пространства относительно операций сложения векторов и векторного произведения векторов, образует кольцо. Так как ( Свойства кольца. 1) Умножение дистрибутивно относительно вычитания, т.е.
Доказательство.
Аналогично доказывается 2-е равенство. 2) Доказательство. Т.к. Утверждение, обратное свойству 2), неверно. А именно, существуют кольца, в которых произведение двух ненулевых элементов равно нулю, т.е Аналогично, 3) Если
Доказательство.
4) Доказательство.
Так же 4°. Поле, свойства поля. Определение 10. Множество 1) (P;+) – абелева группа. 2) (P\{0}; 3) Умножение дистрибутивно относительно сложения, т.е.
Т.о., поле – это коммутативное и ассоциативное кольцо с единицей, в котором все ненулевые элементы составляют мультипликативную группу. Примеры полей. 1) (Q; +, 2) ( Свойства поля. 1) В поле Р нет делителей нуля. Доказательство. Пусть 2) Свойство сокращения на ненулевой элемент: 3) Доказательство. При 2. Понятие многочлена над полем. Множество многочленов как коммутативное кольцо над полем с единицей и без делителей нуля. Делители многочленов, наибольший общий делитель. Алгоритм Евклида построения наибольшего общего делителя многочленов. Определение 1. Многочленом от одной переменной с коэффициентами из поля Множество многочленов с коэффициентами из поля Введем операции сложения и умножения многочленов. Пусть
Очевидно, что Теорема 1. Доказательство. Опр. Непустое множество K с 2-мя операциями сложения и умножения называется кольцом и обозначается (K 1) (K, +) – абелева группа. Абелева (коммутативная) – значит «+» коммутативная операция. Группа: 1.1) + – ассоциативная операция. 1.2) В G 1.3) 2) умножение на множестве K ассоциативно, т.е.
3) умножение дистрибутивно относительно сложения, т.е.
Кольцо называется коммутативным (понятия абелева кольца нет!!!), если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей.
Проверим все эти свойства. 0)Сумма многочленов = многочлен. 1.1) (f+g)+h=f+(g+h) 1.2) Нейтральный (нулевой) элемент e=
1.3) К 2) Проверим ассоциативность умножения. Пусть
Необходимо доказать, что
и
т.е. ассоциативность умножения выполняется. 3) Проверим дистрибутивность, т.е. выполнение равенств
Имеем
Аналогично доказывается второе равенство. 4) Проверим коммутативность умножения. Имеем
5) Легко проверить, что 6) (делители нуля – это, если произведение 2-х не нулевых элементов=0) Покажем, что в
4o. Делители многочленов. Наибольший общий делитель. Определение 3. Пусть Свойства (делимости многочленов). Пусть 1) Если Доказательство. Так как 2) Доказательство. Так как
3) Доказательство. Аналогично 2) 4) Доказательство.
5) Если
6) Доказательство. Если 7) 8) Действительно, ноль представим как 9) Доказательство.
10) Доказательство.
Если
11) Если Определение 4. Многочлен Замечание. Ненулевая постоянная является общим делителем любых двух многочленов. Утверждение 2. Если НОД двух многочленов Доказательство. Пусть Осталось показать, что если НОД Утверждение 3. Если Доказательство. Пусть Лемма 4. Если Доказательство следует из того, что Теорема 3. Для Доказательство. Рассмотрим Если Пусть
Здесь Из равенств ( Если Замечание 1. Алгоритм построения НОД, использованный в теореме 3, называется алгоритмом Евклида или алгоритмом последовательного деления. Замечание 2. Если Замечание 3. Так как НОД определен с точностью до множителя, то будем считать, что коэффициенты при старшей степени равен 1. Пример. Если Замечание 4. При вычислении НОД результаты вычисления можно умножать и делить на элементы из 3. Основная теорема алгебры и следствия из неё (разложимость на множители, единственность разложения и число корней многочлена). Многочлен с действительными коэффициентами. Свойства комплексных корней многочлена с действительными коэффициентами. Теорема 8 (ОТА). Всякий многочлен Доказательство.Первые попытки доказательства этой теоремы в XVII в. – Роте, Жирар, Декарт, в XVIII в. – Д’Аламбер, Эйлер, Лаплас, Лагранж. Первое строгое доказательство в 1799 г. – К.Гаусс. Доказательство см., например, Курош [8]. Следствие 1.
где Доказательство. Пусть В итоге получаем (4), где появление коэффициента Следствие 2. Разложение (4) для многочлена Доказательство.
Тогда имеем равенство:
Если бы корень Отсюда еще не следует совпадение всех корней двух разложений. Может случиться, что среди корней Пусть Объединяя одинаковые множители, разложение (4) перепишем в виде: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  .
. ), где
), где 
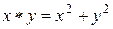 . Такая операция
. Такая операция  коммутативна, но не ассоциативна. Действительно:
коммутативна, но не ассоциативна. Действительно: 
 .
. называется нейтральным относительно алгебраической операции
называется нейтральным относительно алгебраической операции  .
.
 с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей.
с заданной на нем бинарной ассоциативной операцией называется полугруппой. Полугруппа с нейтральным элементом называется моноидом или полугруппой с единицей. моноида
моноида  называется симметричным к элементу
называется симметричным к элементу  , если
, если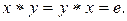
 называют произведением, нейтральный элемент – единицей (обозначают 1), симметричный элемент к
называют произведением, нейтральный элемент – единицей (обозначают 1), симметричный элемент к  – обратным (пишут
– обратным (пишут  ). В случае аддитивной операции результат операции
). В случае аддитивной операции результат операции  ).
). нейтральный элемент
нейтральный элемент  .
.

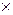 ) – коммутативная полугруппа с нейтральным элементом.
) – коммутативная полугруппа с нейтральным элементом. ) – абелева (коммутативная) полугруппа с нейтральным элементом.
) – абелева (коммутативная) полугруппа с нейтральным элементом. ) – мультипликативная абелева (коммутативная) группа.
) – мультипликативная абелева (коммутативная) группа. – множество непрерывны на
– множество непрерывны на  функций. И пусть
функций. И пусть  . – тогда это абелева группа.
. – тогда это абелева группа. нейтральный элемент и
нейтральный элемент и  (от противного). Пусть
(от противного). Пусть  − два нейтральных элемента
− два нейтральных элемента 
 (по условию нейтральности
(по условию нейтральности 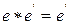 (по условию нейтральности
(по условию нейтральности  .■
.■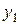 и
и  Тогда в силу (1) и (2) имеем:
Тогда в силу (1) и (2) имеем: .■
.■ уравнения
уравнения 
 имеют единственное решение:
имеют единственное решение: ,
,  . (напоминание:
. (напоминание:  - симметричный элемент к
- симметричный элемент к  )
) . Имеем:
. Имеем:  , т.е.
, т.е. 


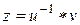
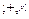 ), если выполняются условия:
), если выполняются условия:
 ,
, 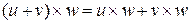 .
. непрерывных на отрезке
непрерывных на отрезке  функций с операциями + и
функций с операциями + и  ,
, ;+) абелева группа, то
;+) абелева группа, то 
 . Поэтому в К можно ввести операцию вычитания:
. Поэтому в К можно ввести операцию вычитания:  .В силу свойства группы
.В силу свойства группы  единственное решение уравнения
единственное решение уравнения  .
. .
. .
. .
. . Аналогично доказывается, что
. Аналогично доказывается, что  .
. но
но 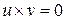 . Такие кольца называются кольцами с делителями нуля. Например, множество
. Такие кольца называются кольцами с делителями нуля. Например, множество  непрерывных функций – кольцо с делителями нуля. Действительно, если
непрерывных функций – кольцо с делителями нуля. Действительно, если 

 ,
, 


 − множество матриц размера
− множество матриц размера  − кольцо с делителями нуля.
− кольцо с делителями нуля. − отличный от нуля элемент из
− отличный от нуля элемент из  (закон сокращения в кольце). Аналогично,
(закон сокращения в кольце). Аналогично, 

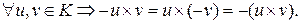


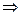
 .
. является симметричным к элементу
является симметричным к элементу  , потому что
, потому что 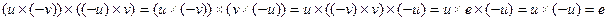 .
. , содержащие не менее двух элементов, с заданными на нём алгебраическими операциями сложения + и умножения
, содержащие не менее двух элементов, с заданными на нём алгебраическими операциями сложения + и умножения  ), если:
), если:
 ,
,  ,
,  Пусть
Пусть  , тогда
, тогда  . Умножим
. Умножим  на
на  :
:  . С другой стороны,
. С другой стороны, 
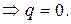
 из
из 
 (уже доказали – 3)свойство для кольца)
(уже доказали – 3)свойство для кольца) , уравнение
, уравнение  в поле P имеет единственное решение
в поле P имеет единственное решение 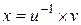 .
. доказываемое свойство – это 2) свойство группы, при
доказываемое свойство – это 2) свойство группы, при  − 2) свойство кольца.
− 2) свойство кольца. , в которой лишь конечное число элементов не равно нулю.
, в которой лишь конечное число элементов не равно нулю.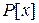 .
. . Тогда
. Тогда ,
, 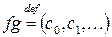 , где
, где  .
. и
и  имеют лишь конечное число ненулевых членов, т.е. являются многочленами.
имеют лишь конечное число ненулевых членов, т.е. являются многочленами.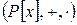 – коммутативное кольцо с единицей и без делителей нуля.
– коммутативное кольцо с единицей и без делителей нуля. – абелева группа – очевидно:
– абелева группа – очевидно: .
.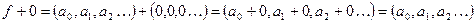
 симметричный элемент
симметричный элемент  .
. 
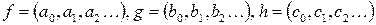 .
. . Имеем:
. Имеем: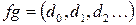 , где
, где  . Тогда
. Тогда , где
, где 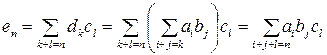 ,
, , где
, где  ,
, .
.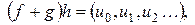 где
где  ;
; где
где  .
.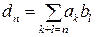 и
и , где
, где 
 силу коммутативности умножения в
силу коммутативности умножения в  – единица в
– единица в  , так как
, так как  .
. ,
,  ,
, 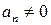 ,
,  ,
,  ,
,  ,
,  ,
,  . Тогда
. Тогда , где
, где  , т.к.
, т.к.  . Если
. Если 
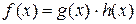 , то говорят, что
, то говорят, что  делится на
делится на  или
или  . Если
. Если 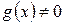 , то
, то  . В этом случае многочлен
. В этом случае многочлен 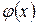 ,
,  ,
,  ,
,  . Тогда справедливы свойства:
. Тогда справедливы свойства: .
. , тогда
, тогда  т.к.
т.к.  .
. ,
,  .
. ; так как
; так как .
. .
.
 выполняется
выполняется  .
.
 . Тогда
. Тогда ; следовательно,
; следовательно,  .
. ,
,  , то справедливо
, то справедливо .
. .
. справедливо представление
справедливо представление  .
. имеем
имеем 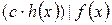 .
.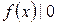 .
.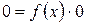 .
. .
.
 и
и  . Ho
. Ho  .
.
 и
и  .
. .
. имеем
имеем 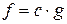 .
. и по свойству 1 имеем
и по свойству 1 имеем  (в силу свойства 9)
(в силу свойства 9)  имеем
имеем  .
. называется общим делителем
называется общим делителем 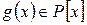 , если
, если  и
и  . Наибольшим общим делителем (НОД) двух многочленов
. Наибольшим общим делителем (НОД) двух многочленов  , который делится на любой другой их общий делитель.
, который делится на любой другой их общий делитель. 
 .
. и
и 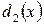 – два НОД для
– два НОД для  и
и 
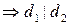 и
и 
 , для
, для  и
и  .
. , то вновь полученное – это НОД. Если
, то вновь полученное – это НОД. Если  – тоже общий делитель, по свойству 7). Если
– тоже общий делитель, по свойству 7). Если  – НОД, т.е. любой другой делитель делит
– НОД, т.е. любой другой делитель делит  − тоже НОД.■
− тоже НОД.■ ,
,  , то пары многочленов
, то пары многочленов 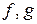 и
и  имеют одинаковые общие делители.
имеют одинаковые общие делители. – общий делитель
– общий делитель  )
) 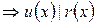 . Аналогично, из делимости
. Аналогично, из делимости  на
на 
 .
. ,
,  НОД(
НОД( 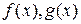 )
)  .
. . Если
. Если  , то в силу Леммы 4 и условия
, то в силу Леммы 4 и условия  имеем
имеем  – НОД(
– НОД(  , то поделим
, то поделим  .
.  , где
, где  . Если
. Если  , то теорема доказана в силу леммы 4.
, то теорема доказана в силу леммы 4. . Тогда делим
. Тогда делим  , то доказательство завершаем, если
, то доказательство завершаем, если 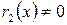 , то делим
, то делим  на
на  и т.д. Так как степени остатков все время уменьшаются, то процесс конечен. Таким образом, имеем следующую последовательность равенств:
и т.д. Так как степени остатков все время уменьшаются, то процесс конечен. Таким образом, имеем следующую последовательность равенств:





 .
. ) и утверждения 3
) и утверждения 3 
 имеют общие делители, т.е.
имеют общие делители, т.е.  является общим делителем многочленов
является общим делителем многочленов  – НОД.■
– НОД.■
 .
.
 , то
, то  .
. , имеет хотя бы один комплексный корень.
, имеет хотя бы один комплексный корень. числа
числа 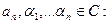 справедливо разложение
справедливо разложение
 − старший коэффициент,
− старший коэффициент,  − корни многочлена
− корни многочлена  .
. По теореме 8
По теореме 8  многочлена
многочлена  где
где  имеет степень
имеет степень  и по ОТА имеет корень
и по ОТА имеет корень 

 .
. , то после раскрытия скобок получим
, то после раскрытия скобок получим  .■
.■ .
. …
…  =
=  …
…  .
. был отличен от всех корней
был отличен от всех корней  , то после подстановки слева получаем 0, а справа – нет
, то после подстановки слева получаем 0, а справа – нет  корню
корню  , есть одинаковые. Пусть
, есть одинаковые. Пусть  − корень кратности
− корень кратности 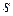 , а соответствующий корень
, а соответствующий корень  − корень кратности
− корень кратности  . Нужно показать, что
. Нужно показать, что  .
. . Т.к.
. Т.к.  − кольцо без делителей нуля, то можно сократить на
− кольцо без делителей нуля, то можно сократить на  приходим к равенству, где слева есть множитель
приходим к равенству, где слева есть множитель  , а справа – нет. Как показано выше, это приводит к противоречию
, а справа – нет. Как показано выше, это приводит к противоречию