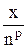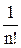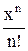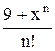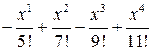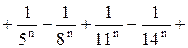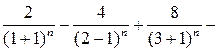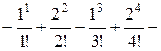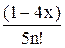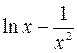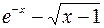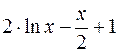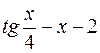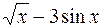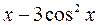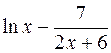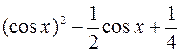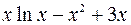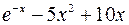Вычисление суммы сходящегося ряда с заданной точностью

Var {раздел объявления переменных}

n: integer; {переменная сходящегося ряда}

term, summa, precision: real; {переменные, означающие соответственно член ряда, сумма ряда, точность вычисления}

BEGIN {начало тела программы}

Writeln('Данная программа вычисляет сумму сходящегося ряда с за данной точностью, каждый член ряда вычисляется по формуле term=1/n'); {оператор вывода, который описывает назначение программы}

Writeln('Введите точность вычисления');

Readln(precision); {ожидание ввода с клавиатуры, введенное значение запишется в переменную precision}

summa:=0; {для того чтобы накапливать сумму в переменной summa, ее необходимо обнулить, так как при выделении памяти в ней может быть любое значение соответствующего типа}

n:=1; {присваиваем первоначальное значение до входа в цикл согласно заданию}

Repeat

term:=1/n; {вычисление текущего значения члена ряда}

summa:=summa+term; {накопление суммы, к предыдущему значению суммы прибавляется текущее значение}

n:=n+1; {к предыдущему значению переменной «n» прибавляем единицу согласно условию задачи}

Until term<=precision; {цикл выполняется до тех пор, пока текущее значение члена ряда не станет меньшим либо равным точности вычисления}

Writeln('Сумма сходящегося ряда с заданной точностью=', summa: 5: 2); {вывод результата с использованием форматирования}

Writeln('Количество членов ряда=', n);

END. {конец программы}

Пример программы, вычисляющей корень уравнения y=x²-5 методом половинного деления

Uses Crt; {подключаем модуль Crt для того, чтобы воспользоваться процедурой очистки экрана ClrScr;}

Var c, Fc, Fb: double;

a, b, e: real;

BEGIN

ClrScr; {очистка экрана}

Writeln(‘Данная программа находит корень уравнения методом половинного деления y=x²-5’);

Writeln(‘Введите значения концов отрезка, на котором имеется один корень, а также точность вычисления’);

Readln(a,b,e);

{цикл выполняется до тех пор, пока разность концов отрезка по модулю будет больше точности вычисления}

While (abs(b-a)>e) Do

Begin

if (keypressed) then halt; {данная строка обозначает, что при нажатии любой клавиши произойдет выход из программы, это нужно для избегания зацикливания, если начальные данные заданны не верно}

c:=(a+b)/2; {находим середину отрезка}

Fc:=sqr(c)-5; {вычисляем значение функции в новой точке “c”}

Fb:=sqr(b)-5; {вычисляем значение функции в точке “b”}

{если произведение значений функций в точках ‘c’ и ’b’ имеют разные знаки, то на этом промежутке находится корень уравнения}

if (Fc*Fb)>0 then b:=c else a:=c;

End; {окончание цикла while}

Writeln('Корень=', c: 6: 5); {вывод результата}

Readln; {задержка для просмотра результата}

END.

Пример программы, вычисляющей корень уравнения y=x²-5 методом касательных

Uses Crt;

Var F, F_, xLast, e, x: double;

BEGIN

ClrScr;

Writeln(‘Данная программа находит корень уравнения методом касательных y=x²-5’);

Writeln(‘Введите значение аргумента первоначального приближения’);

Readln(x);

Writeln(‘Введите значение точности’);

Readln(e);

Repeat

if (keypressed) then halt;

F:=x*x-5; {подсчет значения функции}

F_:=2*x; {подсчет значения производной функции}

xLast:=x; {сохранение предыдущего значения}

x:=xLast - F/F_; {подсчет текущего значения}

Until (abs(xLast-x)<e);

Writeln('Корень=', x: 5: 4);

Readln;

END.

Список заданий

Список заданий на вычисление суммы сходящегося ряда

В списке заданий (табл. 1) ряд может быть представлен как последовательностью членов ряда, так и в общем виде:

Таблица 1

№ вар-та	Задание	№ вар-та	Задание
		16

Окончание табл. 1

№ вар-та	Задание	№ вар-та	Задание

Примечание: x, p – это константы, объявленные в программе.

Список заданий на нахождение корней уравнений

В списке заданий (табл. 2) используются следующие сокращения:

A – метод половинного деления

B – метод Ньютона-Рафсона (метод касательных)

C – модифицированный метод Ньютона (метод хорд)

Таблица 2

№	Уравнение	Метод	№	Уравнение	Метод
		B	16		A
		A			B
		C			B
		A			A
		C			C
		A			B
		B			C
		A			A
		B			B
		C			C
		B			C

Окончание табл. 2

№	Уравнение	Метод	№	Уравнение	Метод
		C			A
		B			C
		A			B
		C			A

5. Контрольные вопросы

1. Какие методы решения задач называют прямыми, а какие итерационными?

2. Когда применяют прямые, а когда итерационные методы при решении задач?

3. Какие методы решения уравнений вы знаете?

4. В чем принцип метода половинного деления?

5. Чем отличается метод касательных от метода хорд?

6. Без каких конструкций языка Паскаль не обходится решение итерационных задач?

Список рекомендуемой литературы

1. Немнюгин, С.А. Turbo Pascal: программирование на языке высокого уровня / С.А. Немнюгин. – 2-е изд. – СПб.: Питер, 2006. – 544с.

2. Немнюгин, С.А. Turbo Pascal: практикум / С.А. Немнюгин. – 2-е изд. – СПб.: Питер, 2006. – 272с.

3. Фаронов, В.В. TurboPascal: учебное пособие / В.В. Фаронов. – М.: Изд.: ОМД Групп, 2007. – 368с.

4. Марченко, А.И. Программирование в среде Turbo Pascal 7.0. / А.И. Марченко, Л.А. Марченко. – М.: Бином Универсал, К.: ЮНИОР, 1997. – 496с.

5. Культин, Н.Б. Turbo Pascal в задачах и примерах / Н.Б. Культин. – СПб.: БХВ-Петербург, 2007. – 256с.

6. Коффман, Э.М. Turbo Pascal / Э.М. Коффман. – 5-е изд. – М.: Вильямс, 2005. – 896с.

7. Рапаков Г.Г. Программирование на языке Pascal: учебное пособие / Г.Г. Рапаков, С.Ю. Ржеуцкая – СПб.: БХВ-Петербург, 2004. – 480с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: