
|
|
Метод половинного деления12 Алгоритмические языки и программирование
Итерационные методы решения задач
Методические указания к выполнению лабораторной работы №3 для студентов очной формы обучения специальности 230201 – "Информационные системы и технологии"
Брянск 2007 УДК 004.43
Алгоритмические языки и программирование. Итерационные методы решения задач: методические указания к выполнению лабораторной работы №3 для студентов очной формы обучения специальности 230201 – "Информационные системы и технологии". – Брянск: БГТУ, 2007. - 12 с.
Разработали: Ю.А. Леонов, асс. С.М. Рощин, к.т.н.
Научный редактор Ю.М. Казаков Редактор издательства Л.И. Афонина Компьютерный набор Ю.А. Леонов Рекомендовано кафедрой «Компьютерные технологии и системы» БГТУ (протокол № от )
Темплан 2007г., п. 458
Издательство брянского государственного технического университета, 241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. 58-82-49 Лаборатория оперативной полиграфии БГТУ, ул. Харьковская, 9 ЦЕЛЬ РАБОТЫ Целью работы является ознакомление с итерационными методами нахождения результата на примере вычисления суммы сходящегося ряда и нахождение корней нелинейных уравнений. Продолжительность работы – 6ч. Теоретическая часть Числовые ряды Если существует конечный предел частичных сумм S=u1+u2+u3+…+un+…, где u1, u2, u3 … - члены сходящегося ряда.
Итерационные методы Для решения систем алгебраических уравнений, нахождения экстремумов функций и т.д. существуют прямые и итерационные методы. Прямые методы позволяют получить точное решение, выполнив конечное число операций. Примером прямого метода может служить правило Крамера для решения системы совместных линейных алгебраических уравнений. Обычно для сложных систем уравнений прямые методы неэффективны, так как при их применении требуется выполнение огромного объема вычислений. Поэтому чаще пользуются итерационными методами. Сущность итерационных методов заключается в многократном повторении одного и того же простого алгоритма, который дает результат, постепенно приближающийся к точному решению. Итерации начинаются с задания начального приближенного решения. Затем начальные значения переменных последовательно изменяются, пока не достигается заданная точность решения. Быстрота сходимости итерационного метода сильно зависит от степени точности начальной аппроксимации.
Решение нелинейных уравнений Любое уравнение можно представить в виде ¦(x)=0, если перенести все компоненты уравнения в одну сторону, тогда поиск корней уравнения сводится к поиску точек пересечения функции ¦(x) с осью абсцисс. В случае, когда невозможно или крайне затруднителен поиск прямых методов решения для нахождения корней нелинейных уравнений, применяют итерационные методы решения. Ниже представлены три итерационных метода решения нелинейных уравнений: метод половинного деления, метод Ньютона (метод касательных) и модифицированный метод Ньютона (метод хорд). Метод половинного деления Существует ряд методов численного решения нелинейных уравнений, целесообразность применения каждого из которых определяется видом уравнения, его порядком, требуемой точностью и т.д. Возможность нахождения корня уравнения заданным методом строится на утверждении, что функция, пересекающая ось абсцисс, имеет различные знаки функции по разные стороны от корня уравнения, если это не так, то заданный метод не может быть применен. В случае, когда функция касается одной точкой оси абсцисс, при этом знак ее не меняется, представленный метод нахождения корней нелинейных уравнений может быть применен, например, для функции y=x2 (рис. 1).
Рис. 1. Графическая интерпретация метода половинного деления
Суть алгоритма нахождения корня уравнения заданным методом можно представить совокупностью повторяющихся операций, называемых итерациями. Алгоритм одной итерации можно представить в следующем виде: · делим отрезок [a,b], на котором имеется один корень уравнения, на две равные части, полученную точку назовем “c” (рис.1); · далее необходимо определить, на каком из полученных отрезков [a,c] или [c,b] находится корень уравнения, на рис.1 хорошо видно, что знаки функции на концах отрезков [a,c] имеют различные знаки, а для отрезка [c,b] одинаковые. Следовательно, корень уравнения находится на том отрезке, где функции для аргументов концов отрезка будут иметь различные знаки. Математически это можно записать так: · после того как мы нашли новый отрезок, задачу можно свести к предыдущей, переименовав точку “c” в точку “b”, так как задача свелась к предыдущей, то можно проделать описанные шаги еще раз; · итерации повторяются до тех пор, пока разница между большим и меньшим значениями отрезка не будет меньшим либо равным точности вычисления 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
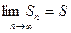 , то числовой ряд называется сходящимся и его сумма равна значению этого предела, иначе ряд называется расходящимся. Если ряд сходится, т.е. имеет сумму S, то пишут
, то числовой ряд называется сходящимся и его сумма равна значению этого предела, иначе ряд называется расходящимся. Если ряд сходится, т.е. имеет сумму S, то пишут

 Пусть дано уравнение ¦(x)=0, где ¦(x)-непрерывная функция, и корень Р отделен на отрезке [a,b]. Требуется найти значение корня Р с точностью Е.
Пусть дано уравнение ¦(x)=0, где ¦(x)-непрерывная функция, и корень Р отделен на отрезке [a,b]. Требуется найти значение корня Р с точностью Е.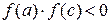 ;
; .
.