
|
|
Метод половинного деления12 Лабораторная работа ЧИСЛЕННОЕ НАХОЖДЕНИЕ ИЗОЛИРОВАННОГО КОРНЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ Решение уравнений – алгебраических или трансцендентных – представляет собой одну из существенных задач прикладного анализа, потребность в которой возникает во многочисленных и самых разнообразных разделах физики, механики, техники и других областях. Пусть дано уравнение f (x) = 0. (1) Всякое число х*, обращающее функцию f (x) в нуль, т.е. такое, при котором f (х*) = 0, называется корнем уравнения (1) или нулем функции f (x). Задача численного нахождения действительных корней уравнения (1) обычно состоит в приближенном нахождении корней, т.е. нахождении достаточно малых окрестностей рассматриваемой области, в которой содержится одно значение корня и, далее, вычислении корней с заданной степенью точности. Пусть
3. Первая и вторая производные f ' (x) и f '' (x) сохраняют определенный знак на всем отрезке. Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что f (x) на данном интервале монотонна и поэтому корень будет единственным. Задача нахождения корня уравнения f (x) = 0 итерационным методом состоит из двух этапов: 1. отделение корней - отыскание приближенного значения корня или содержащего его отрезка; 2. уточнение приближенных корней - доведение их до заданной степени точности. Процесс отделения корней начинается с установления знаков функции f (x) в граничных x = a и x = b точках области ее существования. Пример 1. Отделить корни уравнения: x3 – 6x + 2 = 0 (2) Составим приблизительную схему:
Следовательно, уравнение (2) имеет три действительных корня, лежащих в интервалах [-3, -1], [0, 1] и [1, 3]. Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом. В инженерной практике распространен графический способ определения приближенных корней. Принимая во внимание, что действительные корни уравнения (1) - это точки пересечения графика функции f (x) с осью абсцисс, достаточно построить график функции f (x) и отметить точки пересечения f (x)с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Пусть корень уравнения (1) изолирован на отрезке [a, b]. Итерационный процесс уточнении начального приближения х0 к точному решению состоит в последовательном получении последующего приближение из предыдущего (предыдущих). Каждый такой шаг называется итерацией. Применение того или иного метода зависит от имеющегося начального приближения х0 к корню, существования и гладкости производных функции f (x). В результате итераций находится последовательность приближенных значений корня х1, х2, ..., хn. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится. В итерационных методах важно выбрать критерий окончания счета. Если функция f (x) в рассматриваемой области изменяется медленно, т.е. производная по абсолютной величине меньше единицы, то итерационный процесс следует оканчивать по выполнению условия | xk+1 – xk | < ε, где xk , xk+1 – последовательные приближения к корню, ε > 0 – заданная точность окончания итерационного процесса. Если же функция изменяется быстро, т.е. | f ´ (x) | ≥ 1, то итерационный процесс следует оканчивать по выполнению условия | f (xk) | < ε. Метод половинного деления Этот метод является одним из простейших итерационных методов вычисления вещественного корня уравнения (1) на отрезке [α, β]. Его применяют, когда f (x) непрерывна на [α, β] и на концах этого отрезка принимает значения разных знаков, т.е. f (α) · f (β) < 0. Вычислительная схема метода. Отрезок [α, β] делят пополам и если f | xk+1 – xk | < ε. Число итераций k в методе половинного деления определяется по формуле k ≈ Пример 1. Методом половинного деления вычислить корень уравнения х3 + 3х2 – 1 = 0 (2) с точностью 0,01 на отрезке [0, 1]. Проверяем условия применимости метода. Функция f (x) является полиномом третьей степени (непрерывна) и f (0) · f (1) < 0. Вычисляем последовательно приближения к корню и проверяем их по точности:
Примем за уточненное значения корня величину х* =
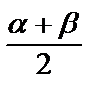 находим середину отрезка [α, β]. Вычисление величины f находим середину отрезка [α, β]. Вычисление величины f  означает восстановление перпендикуляра из точки означает восстановление перпендикуляра из точки  до пересечения с графиком функции f (x). Если | xk+1 – xk | > ε, то для дальнейшего рассмотрения оставляем тот отрезок, на концах которого f (x) принимает значения разных знаков. В нашем случае это отрезок до пересечения с графиком функции f (x). Если | xk+1 – xk | > ε, то для дальнейшего рассмотрения оставляем тот отрезок, на концах которого f (x) принимает значения разных знаков. В нашем случае это отрезок  . На этом шаг итерационного процесса оканчивается. Повторяем итерации до тех пор, пока не будет выполнено условие окончания счета. . На этом шаг итерационного процесса оканчивается. Повторяем итерации до тех пор, пока не будет выполнено условие окончания счета.
Рис.1. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ≠ 0, то выбирают ту из половин
≠ 0, то выбирают ту из половин  ,
,  , на концах которой функция f (x) принимает значения разных знаков (корень находится в ней). Полученный отрезок опять делят пополам и повторяют описанные действия до тех пор, пока не получат корень с заданной точностью итерационного процесса. Процесс оканчивается по выполнению условия
, на концах которой функция f (x) принимает значения разных знаков (корень находится в ней). Полученный отрезок опять делят пополам и повторяют описанные действия до тех пор, пока не получат корень с заданной точностью итерационного процесса. Процесс оканчивается по выполнению условия .
. = 0,53515625.
= 0,53515625.

