
|
|
Переход от одной прямоугольной декартовой системы координат к другойВыбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка. Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится рассматривать в разных координатных системах. Одна и та же точка в разных системах имеет, очевидно, различные координаты. Множество точек (в частности, окружность, парабола, прямая) в разных системах координат задается различными уравнениями. Выясним, как преобразуются координаты точек плоскости при переходе от одной координатной системы к другой. Пусть на плоскости заданы две прямоугольные системы координат: О, i, j и О', i', j' (рис. 41).
Первую систему с началом в точке О и базисными векторами i и j условимся называть старой, вторую — с началом в точке О' и базисными векторами i' и j' — новой. Положение новой системы относительно старой будем считать известным: пусть точка О' в старой системе имеет координаты (a;b), a вектор i' образует с вектором i угол α. Угол α отсчитываем в направлении, противоположном движению часовой стрелки. Рассмотрим произвольную точку М. Обозначим ее координаты в старой системе через (х;у), в новой — через (х';у'). Наша задача — установить зависимость между старыми и новыми координатами точки М. Соединим попарно точки О и О', О' и М, О и М. По правилу треугольника получаем OM> = OO'> + O'M>. (1) Разложим векторы OM> и OO'> по базисным векторам i и j, а вектор O'M> по базисным векторам i' и j' : OM> = xi + yj, OO'>= ai + bj , O'M> = x'i '+ y'j' Теперь равенство (1) можно записать так: xi + yj = (ai + bj) + ( x'i '+ y'j' ). (2) Новые базисные векторы i' и j' раскладываются по старым базисным векторам i и j следующим образом: i' = cos α i + sin α j, j' = cos (π/2 + α) i + sin ( π/2 + α) j = — sin α i + cos α j. Подставив найденные выражения для i' и j' в формулу (2), получим векторное равенство xi + yj = ai + bj+ х'(cos α i + sin α j) + у' (— sin α i + cos α j) равносильное двум числовым равенствам:
Формулы (3) дают искомые выражения для старых координат х и у точки через ее новые координаты х' и у'. Для того чтобы найти выражения для новых координат через старые, достаточно решить систему уравнении (3) относительно неизвестных х' и у'. Итак, координаты точек при переносе начала координат в точку (а; b) и повороте осей на угол α преобразуются по формулам (3). Если изменяется только начало координат, а направления осей остаются прежними, то, полагая в формулах (3) α = 0, получаем
Эти формулы кратко называют формулами переносa. Если начало координат остается прежним, а оси поворачиваются на угол α, то, полагая в формулах (3) а = b = 0, получаем
Формулы (5) называют формулами поворота. Задача 1. Пусть координаты нового начала в старой системе (2; 3), а координаты точки А в старой системе (4; —1). Найти координаты точки А в новой системе, если направления осей остаются прежними. По формулам (4) имеем
Ответ. A (2; —4) Задача 2. Пусть координаты точки Р в старой системе (—2; 1), а в новой системе, направления осей которой те же самые, координаты этой точки (5; 3). Найти координаты нового начала в старой системе. А По формулам (4) получаем
откуда а = — 7, b = — 2. Ответ. (—7; —2). Задача 3.Координаты точки А в новой системе (4; 2). Найти координаты этой точки в старой системе, если начало координат осталось прежним, а оси координат старой системы повернуты на угол α = 45°. По формулам (5) находим
Задача 4.Координаты точки A в старой системе (2 √3 ; — √3 ). Найти координаты этой точки в новой системе, если начало координат старой системы перенесено в точку (—1;—2), а оси повернуты на угол α = 30°. По формулам (3) имеем
Решив эту систему уравнений относительно х' и у', найдем: х' = 4, у' = —2. Ответ. A (4; —2). Задача 5. Дано уравнение прямой у = 2х — 6. Найти уравнение той же прямой в новой системе координат, которая получена из старой системы поворотом осей на угол α = 45°. Формулы поворота в данном случае имеют вид
Заменив в уравнении прямой у = 2х — 6 старые переменные х и у новыми, получим уравнение √2/2 ( x' + y' ) = 2•√2/2 ( x' — y' ) — 6 , которое после упрощений принимает вид y' = x'/3— 2√2 У этого термина существуют и другие значения, см. Цепи_Маркова#Переходная матрица и однородные цепи. Ма́трицей перехо́да от базиса Обозначается Определение. Матрица
Лемма. Пусть Теорема.
Теорема. Если Определение. Биекция Следствие. Справедливы равенства Определение. Два линейных пространства называются изоморфными, если существует изоморфизм одного пространства на другое. Теорема. Два конечномерных пространства над полем Следствие. Любое 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


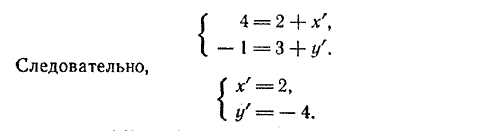
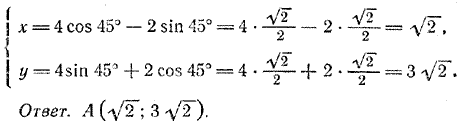


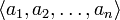 к базису
к базису  является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов 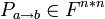
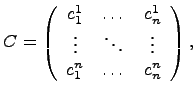
 -ый столбец которой составлен из координат вектора
-ый столбец которой составлен из координат вектора  в базисе
в базисе  , называется матрицей перехода от базиса
, называется матрицей перехода от базиса  . Имеем
. Имеем  .
. и
и  -- матрицы размера
-- матрицы размера  над полем
над полем  , причем
, причем  . Тогда
. Тогда  .
. Матрица перехода
Матрица перехода  от базиса
от базиса  Для любого базиса
Для любого базиса  существует и при том единственный базис
существует и при том единственный базис  справедливо равенство
справедливо равенство  , где
, где  и
и 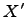 -- столбцы координат вектора
-- столбцы координат вектора  в базисах
в базисах  .
. линейного пространства
линейного пространства  над полем
над полем  над полем
над полем  для любых векторов
для любых векторов  и
и  .
. ,
,  и
и  . Если система
. Если система  линейна независима, то система
линейна независима, то система 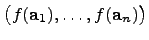 тоже линейна независима. Отображение
тоже линейна независима. Отображение 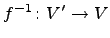 -- изоморфизм.
-- изоморфизм. .
. . Отображение
. Отображение  определено так:
определено так:  .
.