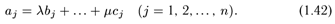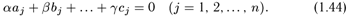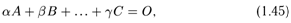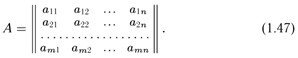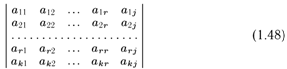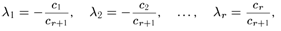|
Теорема о базисном миноре матрицы
1. Понятие линейной зависимости строк. Выше мы уже договорились называть строку A=(a1,a2,...,an) линейной комбинацией
строк В = (b1, b2,..., bn),..., С = (с1, с2,..., сn), если для некоторых вещественных чисел λ,...,µ справедливы равенства
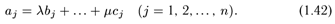
Указанные n равенств (1.42) удобно записать в виде одного равенства

Всякий раз, когда будет встречаться равенство (1.43), мы будем понимать его в смысле n равенств (1.42).
Введем теперь понятие линейной зависимости строк.
Определение. Строки A=(a1,a2,...,an), В = (b1, b2,..., bn),..., С = (с1, с2,..., сn) назовем линейно зависимыми, если найдутся такие числа α, β,..., γ не все равные нулю, что справедливы равенства
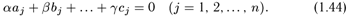
Указанные n равенств (1.44) удобно записать в виде одного равенства
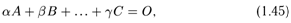
в котором О = (0,0,...,0) обозначает нулевую строку.
Строки, не являющиеся линейно зависимыми, называются линейно независимыми. Можно дать и «самостоятельное» определение линейной независимости строк: строки А, В,..., С называются линейно независимыми, если равенство (1.45) возможно лишь в случае, когда все числа α, β,..., γ равны нулю.
Докажем следующее простое, но важное утверждение.
Теорема 1.5. Для того чтобы строки A, В,..., С были линейно зависимы, необходимо и достаточно, чтобы одна из этих строк являлась линейной комбинацией остальных строк.
Доказательство. 1) Необходимость. Пусть строки A, В, ...,С линейно зависимы, т.е. справедливо равенство (1.45), в котором хотя бы одно из чисел α, β,..., γ отлично от нуля.
Ради определенности допустим, что а ≠ 0. Тогда, поделив (1.45) на α и введя обозначения λ = - β/α ,..., µ = -γ/α , мы можем переписать (1.45) в виде

а это и означает, что строка А является линейной комбинацией строк В,..., С.
2) Достаточность. Пусть одна из строк (например, А) является линейной комбинацией остальных строк. Тогда найдутся числа
-1, λ,...,µ такие, что справедливо равенство (1.46). Но это последнее равенство можно переписать в виде (здесь О = 0,0,...,0) — нулевая строка).
(-1)A + λB + ... + µC = O.
Так как из чисел -1, λ,...,µ одно отлично от нуля, то последнее равенство устанавливает линейную зависимость строк А, В,..., С.
Теорема доказана.
Конечно, во всех проведенных выше рассуждениях термин «строки» можно заменить термином «столбцы».
2.Теорема о базисном миноре. Рассмотрим произвольную (не обязательно квадратную) матрицу
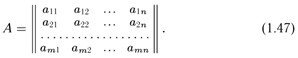
Минором k-го порядка матрицы А будем называть определитель k-го порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А. (Конечно, k не превосходит наименьшее из чисел т и п.)
Предположим, что хотя бы один из элементов аij матрицы А отличен от нуля. Тогда найдется такое целое положительное число r, что будут выполнены следующие два условия: 1) у матрицы А имеется минор r-го порядка, отличный от нуля, 2) всякий минор
(г + 1)-го и более высокого порядка (если таковые существуют) равен нулю.
Число г, удовлетворяющее требованиям 1) и 2), назовем рангом матрицы А (ранг матрицы А, все элементы которой — нули, по определению равен нулю). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (конечно, у матрицы А может быть несколько миноров r-го порядка, отличных от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
Докажем следующую основную теорему.
Теорема 1.6 (теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов).
Доказательство.Все рассуждения проведем для строк.
Если бы базисные строки были линейно зависимы, то по теореме 1.5 одна из этих строк являлась бы линейной комбинацией других базисных строк, и мы могли бы, не изменяя величины базисного минора, вычесть из этой строки указанную линейную комбинацию и получить строку, целиком состоящую из нулей, а это противоречило бы тому, что базисный минор отличен от нуля. Итак, базисные строки линейно независимы.
Докажем теперь, что любая строка матрицы А является линейной комбинацией базисных строк. Так как при произвольных переменах строк (или столбцов) определитель сохраняет свойство равенства нулю, то мы, не ограничивая общности, можем считать, что базисный минор находится в левом верхнем углу матрицы (1.47), т.е. расположен на первых г строках и первых г столбцах. Пусть j — любое число от 1 до n, а k — любое число от 1 до m.
Убедимся в том, что определитель (г + 1)-го порядка
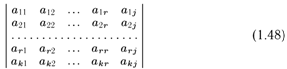
равен нулю. Если j ≤ r или k ≤ r, то указанный определитель будет равен нулю в силу того, что у него будет два одинаковых столбца или две одинаковые строки.
Если же оба числа j и k превосходят г, то (1.48) является минором матрицы А порядка (г + 1), а всякий такой минор равен нулю (по определению базисного минора). Итак, определитель (1.48) равен нулю при всех j от 1 до n и всех k от 1 до m.
Но тогда, разложив этот определитель по последнему столбцу и обозначив не зависящие от номера j алгебраические дополнения элементов этого столбца символами A1j = с1, A2j = c2, ..., Arj = сr, Akj = cr+1, мы получим, что
c1a1j + c2a2j + ... +crarj + cr+1akj = 0
(для всех j = 1, 2,..., n). Учитывая, что в последних равенствах алгебраическое дополнение cr+1 = Akj совпадает с заведомо отличным от нуля базисным минором, мы можем поделить каждое из этих равенств на cr+1. Но тогда, вводя обозначения
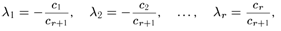
мы получим, что akj= λ1a1j + λ2a2j + ... + λrarj (для всех j = 1, 2,..., n), а это и означает, что k-я строка является линейной комбинацией первых r (базисных) строк. Теорема доказана.
3. Необходимое и достаточное условие равенства нулю определителя.
Теорема 1.7. Для того чтобы определитель n-го порядка А был равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.
Доказательство. 1) Необходимость. Если определитель n-го порядка А равен нулю, то базисный минор его матрицы имеет порядок r, заведомо меньший n. Но тогда хотя бы одна из строк является не базисной. По теореме 1.6 эта строка является линейной комбинацией базисных строк. В эту линейную комбинацию мы можем включить и все оставшиеся строки, поставив перед ними нули.
Итак, одна строка является линейной комбинацией остальных.
Но тогда по теореме 1.5 строки определителя линейно зависимы.
2) Достаточность. Если строки А линейно зависимы, то по теореме 1.5 одна строка Аi является линейной комбинацией остальных
строк. Вычитая из строки Аi указанную линейную комбинацию, мы, не изменив величины А, получим одну строку, целиком состоящую из нулей. Но тогда определитель А равен нулю (в силу следствия 3 из п. 4 §2). Теорема доказана.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|