
|
|
БАЗИС И АФФИННЫЕ КООРДИНАТЫ. ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ12 ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Направленные отрезки. Понятие вектора. Отрезок AB называется направленным, если указано, какая из точек A или B является его началом, а какая концом. Если A – начало, а B – конец, то этот отрезок обозначается , а на чертеже его конец обозначается стрелочкой. Длиной направленного отрезка называется длина отрезка AB. Направленные отрезки и называются сонаправленными (противоположно направленными), если лучи AB и A1B1 сонаправлены (противоположно направлены). Пишем (¯). Два направленных отрезка и называются эквивалентнымиили равными, если они сонаправлены и имеют одинаковую длину. Пишем ~. Очевидно, ~ тогда и только тогда они совмещаются параллельным переносом. Легко проверить, что данное отношение, определенное на множестве всех направленных отрезков плоскости или пространства обладает следующими свойствами: 1.~ (рефлексивность), 2.~ Û ~ (симметричность), 3.(~ & ~)Þ ~ (транзитивность). Таким образом, отношение, которое мы определили, действительно является отношением эквивалентности. Поэтому множество всех направленных отрезков распадается на непересекающиеся классы эквивалентных друг другу отрезков. Вектором называется класс эквивалентных между собой направленных отрезков. Другими словами, каждый направленный отрезок задает вектор, при этом, эквивалентные отрезки задают один и тот же вектор. Направление всех отрезков данного класса называется направлением вектора, а их длина – длиной вектора. Длина вектора обозначается ½½ . Если вектор задается направленным отрезком , то пишем = , и говорим, что есть вектор , отложенный из точки A . На чертеже вектор изображается любым из задающих его направленных отрезков. Пусть задан направленный отрезок и произвольная точка A1. Тогда существует одна и толькоодна точка B1, такая что ~. Другими словами, данный вектор можно отложить из любой точки, и притом,единственным образом. Вектор, длина которого равна нулю, называется нулевым и обозначается . Вектор, длина которого равна 1, называется единичным. Векторы и называются сонаправленными (противоположно направленными), если задающие их направленные отрезки сонаправлены (противоположно направлены). Пишем ( ¯ ). Два вектора, направления которых совпадают или противоположны, называются коллинеарными. Пишем ||. Считается, что у направление неопределено и он коллинеарен любому вектору. Три и более векторов, параллельных одной плоскости называются компланарными. 2. Линейные операции над векторами. Свойства операции сложения векторов. " , , выполнено 1. + = + (коммутативность); 2. ( + ) + = (ассоциативность); 3. + = . 4.$! такой что + = . Этот вектор называетсяпротивоположным вектором к и обозначается – . Разностью двух векторов и называется такой вектор , что + = . Пишем = – . Произведением вектора на число l называется такой вектор , что 1. , если l > 0, и ¯ , если l < 0 ; 2. | |= |l|·| |. Пишем = l. (Часто еще добавляют 3.если l = 0, то = . Но это следует из 2.) Свойства операции умножения вектора на число. 1.l( + ) = l + l; 3.(l + m) = l + m; 2.l(m ) = (lm); 4.1· = . Теорема.(Первый признак коллинеарности векторов). Для того, чтобы ненулевые векторы и были коллинеарны, необходимо и достаточно, чтобы существовало такое число l , что = l. Вектор = называется ортом вектора. 3. Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве. Пусть и – два ненулевых вектора. Отложим их из одной точки О: = , = . Тогда углом между векторами и называется угол между лучами OA и OB, т.е. a =ÐAOB. Пишем a =Ð( , ). Если речь идет о векторах на плоскости, то можем ввести понятие ориентированного угла между векторами. Если крачайший поворот от луча OA к лучу OB осуществляется против часовой стрелки, то считаем, что a > 0, а если по часовой – то a < 0 . Таким образом, – p < a £ p . Если a > 0, то пара векторов (, ) называется правой, а если a < 0 – то левой. Пусть в пространстве даны три некомпланарных вектора , , . Отложим их из одной точки О: = , = , = . Тройка векторов (, , ) называется правой, если кратчайший поворот от луча OA к лучу OB, если смотреть из точки C , выглядит как осуществляющийся против часовой стрелки. Соответственно, если этот поворот выглядит как осуществляющийся по часовой стрелке, то тройка векторов (, , ) называется левой. Замечание 1. Цикличная перестановка векторов (, , ) не меняет ориентации тройки,то есть после цикличной перестановки она остается либо правой, либо левой. Замечание 2.Тройки компланарных векторов не относят ни к правым, ни к левым.
БАЗИС И АФФИННЫЕ КООРДИНАТЫ. ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
1.Линейная зависимость и линейная независимость системы векторов. Линейной комбинацией векторов Если все коэффициенты линейной комбинации равны нулю Система векторов Система векторов
Теорема. (Критерий линейной зависимости системы векторов линейного пространства). Для того, чтобы система векторов линейного пространства была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных векторов системы. Свойства линейно зависимых и линейно независимых систем векторов. 1. Всякая система векторов, включающая нулевой вектор, является линейно зависимой. 2. Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой. 3. Всякая подсистема линейно независимой системы векторов является линейной независимой. Теорема. Для того, чтобы система, состоящая из одного вектора, была линейно зависимой необходимо и достаточно, чтобы он был нулевым вектором. Теорема. (О линейной зависимости двух векторов). Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Теорема. (О линейной зависимости трех векторов). Три геометрических вектора линейно зависимы тогда и только тогда, когда они компланарны. Следствие.Если векторы Теорема. (О линейной зависимости четырех векторов). Четыре геометрических вектора линейно зависимы. Следствие. Если векторы 2.Базисом пространства называется линейно независимая упорядоченная совокупность векторов такая, что любой вектор пространства является линейной комбинацией векторов этой системы. Размерностью векторного пространства называется количество векторов в любом его базисе. Базисом пространства V1 векторов, расположенных на прямой, является любой ненулевой вектор этого пространства. Размерность пространства V1 равна 1. Базисом пространства V2 векторов, расположенных на плоскости, является любая пара некомпланарных векторов этого пространства. Размерность пространства V2 равна 2. Базисом пространства V3 векторов, расположенных в пространстве, является любая тройка некомпланарных векторов. Размерность пространства V3 равна 3. Пусть
называется разложением вектора Теорема. (О разложении вектора по базису). Всякий вектор может быть разложен по некоторому базису векторного пространства единственным образом. Замечание.Из данной теоремы следует, что координаты данного вектора в заданном базисе определяются однозначно. Теорема. (Линейные операции с векторами в координатной форме). При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это же число. Следствие. (Критерий коллинеарности векторов). Для того, чтобы два геометрических вектора были коллинеарными, необходимо и достаточно, чтобы их соответствующие координаты в некотором базисе были пропорциональными. Базис Замечание. Ортонормированный базис в пространстве V2 обычно обозначается Аффинной системой координат (репером) в пространстве Аффинная система координат в пространстве Аффинными координатами точки Так как координаты вектора 3.Деление отрезка в данном отношении. Пусть точка C лежит на отрезке AB. Говорим, что C делит отрезок AB в отношении l1:l2 , если = Û l2½AC½= l1½CB½. Учитывая, что , последнее равенство можно переписать так: l2 = l1. Будем говорить, что точка C делит отрезок AB в отношении l1:l2 , если выполненоl2 = l1. Такое определение означает, что C может лежать на прямой AB за пределами отрезка AB, если l1:l2 отрицательно. Число l = l1/l2 ( = l) называется простым отношением точек A, B, C и обозначается (AB, C) или (ABC). Пусть нам известны координаты концов отрезка: A(x1, y1, z1), B(x2, y2, z2). Требуется найти координаты точки C(x, y, z), которая делит этот отрезок в отношении l1:l2. Из равенства l2 = l1 следует, что x= , y= , z= . В частности, если C делит отрезок AB пополам, то x = , y = , z = . 4.Ортогональная проекция вектора на направление. Осью будем называть прямую, на которой заданы начало отсчета, масштаб (единица длины) и положительное направление. Ортогональной проекцией вектора Проекцию вектора Свойства ортогональной проекции вектора на направление. 1.Проекция вектора на направление равна произведению его длины на косинус угла между вектором и положительным направлением оси: 2. Проекция суммы векторов на направление l равна сумме проекций слагаемых на это направление: 3. Проекция произведения вектора

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 с коэффициентами
с коэффициентами 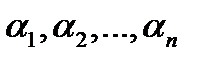 называется вектор
называется вектор  . Здесь
. Здесь 
 , то она называется тривиальной. Если же среди коэффициентов линейной комбинации найдется хотя бы один отличный от нуля, то она называется нетривиальной.
, то она называется тривиальной. Если же среди коэффициентов линейной комбинации найдется хотя бы один отличный от нуля, то она называется нетривиальной.

 и
и  неколлинеарны, и вектор
неколлинеарны, и вектор  компланарен с векторами
компланарен с векторами  и
и  такие, что
такие, что  .
. линейно выражается через векторы
линейно выражается через векторы  такие, что
такие, что  .
. - базис пространства V3. Представление геометрического вектора
- базис пространства V3. Представление геометрического вектора 
 называются координатами вектора
называются координатами вектора  ,
,  ,
, 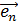 , где
, где  , называетсяортонормированным,если вектора базиса1) имеют единичную длину и, в случае
, называетсяортонормированным,если вектора базиса1) имеют единичную длину и, в случае  , 2) попарно перпендикулярны.
, 2) попарно перпендикулярны. , в пространстве V3 -
, в пространстве V3 -  .
. (на плоскости
(на плоскости  называется совокупность точки О и базиса
называется совокупность точки О и базиса 
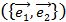 , приведенного к общему началу. Точка O называется началом координат, оси, проходящие через начало координат и определенные векторами
, приведенного к общему началу. Точка O называется началом координат, оси, проходящие через начало координат и определенные векторами  ,
, 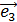 , называются осями координат и обозначаются
, называются осями координат и обозначаются  (ось абсцисс),
(ось абсцисс),  (ось ординат),
(ось ординат), 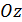 (ось аппликат) соответственно. Плоскость, определяемая осями координат
(ось аппликат) соответственно. Плоскость, определяемая осями координат  и
и 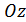 ,
, 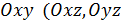 соответственно). В этой терминологии аффинная система координат обозначается также символом
соответственно). В этой терминологии аффинная система координат обозначается также символом  .
. в пространстве (на плоскости) в данной аффинной системе координат
в пространстве (на плоскости) в данной аффинной системе координат  относительно базиса
относительно базиса 
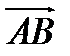 на направление (ось) l называется число, равное длине отрезка A1B1, где A1 и B1 - основания перпендикуляров, опущенных из концов вектора
на направление (ось) l называется число, равное длине отрезка A1B1, где A1 и B1 - основания перпендикуляров, опущенных из концов вектора  совпадает с направлением l и со знаком минус, если направление вектора
совпадает с направлением l и со знаком минус, если направление вектора  .
. , где
, где  .
.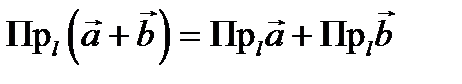 .
. .
.