
|
|
Какое из нескольких возможных событий появилось?
Пусть имеется полная группа несовместных событий: А1, A2,,…, Аk с вероятностями p1 ,р2,, …, рk.
Так как события несовместны и образуют полную группу, то
Разделим весь интервал от 0 до 1 на k участков длиной p1 ,р2,, …, рk .(рис. 8.2). Если случайное число R, выданное стандартным механизмом, попало, например, на участок p3,это означает, что появилось событие A3.
3. Какое значение примет случайная величина? Пусть нам требуется «разыграть» значение случайной величины X, имеющей известный закон распределения. Случай, когда величина X дискретна (т. е. имеет отдельные значения x1,x2,...,xk с вероятностями p1,p2,...,pk) рассматривать не будем, так как он сводится к предыдущему пункту 2. Действительно, если обозначить Ai событие, состоящее в том, что величина X приняла значение xi,то розыгрыш значения случайной величины X сводится к решению вопроса: какое из событий А1, A2,,…, Аk появилось?
Рассмотрим случай, когда случайная величина Х непрерывна и имеет заданную непрерывную функцию распределения F(x) (рис. 8.3).
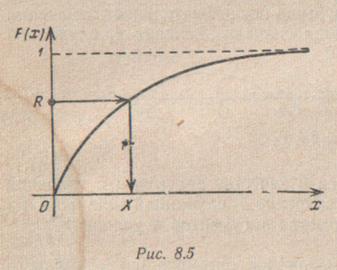
Докажем следующее утверждение: если взять на оси ординат случайное число R (от 0 до 1) и найти то значение X, при котором F(X) = R (см. стрелки на рис. 8.3), то полученная случайная величина X будет иметь функцию распределения F(x). Действительно, возьмем случайную величину X и найдем ее функцию распределения, т. е. вероятность Р(Х<х). Из рисунка видно, что для того чтобы выполнялось неравенство X < х, величина R должна принять значение, меньшее, чем F(x): Р(X<x) = P(R<F(x)). Но случайное число R имеет постоянную плотность распределения f(r), равную 1 на отрезке (0, 1); значит,
что и требовалось доказать. Таким образом, розыгрыш значения случайной величины X с заданной функцией распределения F(x) сводится к следующей процедуре. Получить случайное число R от 0 до 1 и в качестве значения X взять: X=F−1 (R), где F−1 — функция, обратная по отношению к F. 4. Какую совокупность значений примет система случайных величин? Пусть имеется система случайных величин: Если случайные величины независимы, то
и розыгрыш совокупности значений системы сводится к тому, чтобы разыграть каждую из них в отдельности, т. е. организовать п единичных жребиев типа, описанного в п. 3. Если случайные величины зависимы, то
где каждая последующая плотность распределения берется условная, при условии, что предыдущие случайные величины приняли определенные значения. При розыгрыше последовательности значений случайных величин получается сначала значение х1 случайной величины Х1;это значение берется в качестве аргумента в условной плотности f(x2/x1); разыгрывается значение х2 случайной величины Х2, оба значения х1, х2 берутся в качестве аргументов в условной плотности f(x3/x1, х2) и т. д. Рассмотрим несколько примеров на организацию единичного жребия.
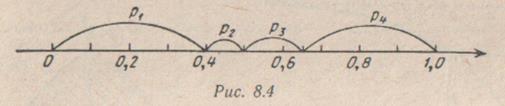
Пример 1. Летательный аппарат, совершающий полет над территорией противника, после стрельбы по нему может оказаться в одном из следующих состояний: А1 — невредим, продолжает полет; А2 — поврежден, продолжает полет; А3 —совершил вынужденную посадку; А4 — сбит. Вероятности этих четырех событий заданы: р1 = Р(А1) = 0,4; р2 = Р(А2) = 0,1;р3 = Р(А3) = 0,15; р4 = Р(А4) = 0,35. Построить процедуру единичного жребия для розыгрыша результата обстрела.
Решение. Делим участок (0, 1) на четыре части, как показано на рисунке.
При попадании случайного числа Rна участок от 0 до 0,4 считать, что произошло событие А1, на участок от 0,4 до 0,5 — событие А2и т. д. Пример 2. Случайная величина X распределена по показательному закону с плотностью:
Построить процедуру единичного жребия для получения значения X.
Решение. По заданной плотности f(x)находим функцию распределения:
График функции F(x)дан на рисунке.
Графически значение случайной величины Xможно разыграть так: взять случайное число от 0 до 1 на оси ординат и найти соответствующее ему значение абсциссы X (см. стрелки на рисунке). Это же можно сделать не графически, а расчетом, если написать:
и решить это уравнение относительно X (т. е. найти обратную по отношению к Fфункцию). Имеем:
откуда
Формулу (2.4) можно упростить; вспомним, что если R—случайное число от 0 до 1, то (1 — R) — также случайное число от 0 до 1; поэтому можно взять
Таким образом, процедура розыгрыша сводится к следующему: взять случайное число от 0 до 1, прологарифмировать его при натуральном основании, изменить знак и разделить на λ.
Пример 3. Построить процедуру розыгрыша значения случайной величины X, плотность распределения которой
Решение. Находим функцию распределения:
График функции распределения имеет вид:
Там же показана процедура розыгрыша значения случайной величины X. Аналитически это выражается так:
откуда обратная функция
Х =агс sin (2R- 1).
Таким образом, для розыгрыша значения случайной величины Xнужно: взять случайное число от 0 до 1, удвоить его, вычесть единицу и от результата взять арксинус.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
.
 ,
, с совместной плотностью распределения
с совместной плотностью распределения 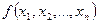 .
. ,
, ,
,

 .
.

 ;
;  ,
, .
. .
. при
при 

 .
.
 ,
,