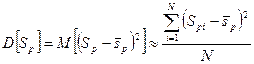Тема 25. Имитационное моделирование. Метод Монте-Карло. Пример, иллюстрирующий метод.

Тема 24. Математические модели операций. Аналитическое и имитационное моделирование.

Аналитические и имитационные модели стохастических систем. В качестве показателей свойств стохастических систем выступают стохастические характеристики соответствующих (случайных) выходов системы, такие как математическое ожидание, дисперсия, ковариационная матрица, вероятность попадания в допустимую область, квантиль и другие. Эти статистические характеристики могут рассчитываться при моделировании стохастической системы двумя способами: аналитически или путем имитации процесса функционирования системы. Соответствующие модели стохастических систем называют аналитическими и имитационными. В литературе имитационное моделирование систем называют также статистическим моделированием или моделированием по методу Монте-Карло.

Мы хорошо знакомы с методами построения некоторых математических моделей, дающих возможность установить аналитическую (формульную) связь между заданными условиями операции (в том числе принятым нами решением) и результатом (исходом) операции, характеризующимся одним или несколькими параметрами — показателями эффективности. Если в ход операции вмешиваются случайные факторы, то она представляет собой случайный процесс, а показатель эффективности — вероятность какого-то события или же математическое ожидание какой-го случайной величины. Иногда удается построить аналитическую модель случайного процесса (например, систему дифференциальных) уравнений для вероятностей состояний или алгебраических уравнений для предельных вероятностей состояний) и связать заданные условия операции с ее исходом аналитическими зависимостями. Однако это удается далеко не всегда, — главным образом, в тех случаях, когда случайный процесс, протекающий в рассматриваемой системе, марковский или близок к марковскому.

На практике далеко не все случайные процессы, наблюдаемые в операциях, являются марковскими или близкими к ним. Например, и реальных системах массового обслуживания поток заявок отнюдь не всегда бывает пуассоновским; еще реже наблюдается показательное (или близкое к нему) распределение времени обслуживания. Для произвольных же потоков событий, переводящих систему из состояния в состояние, аналитические решения получены только для отдельных частных случаев, а в общем случае удовлетворительных методов математического описания соответствующих процессов не существует.

В тех случаях, когда построение аналитической модели явления по той или другой причине трудно осуществимо, применяется другой метод моделирования, известный под названием метода статистических испытаний или, иначе, метода Монте-Карло.

Внастоящее время при имитационном моделировании операций и вообще случайных процессов метод статистических испытаний применяется очень широко. Такое широкое распространение метода связано, главным образом, с появлением ЭЦВМ, позволяющих в обозримые сроки выполнять массовые расчеты по этому методу (без машин весьма трудоемкие). Однако в принципе метод Монте-Карло может применяться и без помощи ЭЦВМ. В данном параграфе мы изложим существо метода, безотносительно к способу его осуществления.

Идея метода Монте-Карло чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать случайное явление с помощью аналитических зависимостей, производится "розыгрыш" — моделирование случайного явления с помощью некоторой процедуры, дающей случайный результат. Так же как в жизни конкретное осуществление процесса складывается каждый раз по-иному, так же и в результате «розыгрыша» мы получаем один экземпляр — одну «реализацию» случайного явления. Произведя такой «розыгрыш» очень большое число раз, мы получим статистический материал — множество реализаций случайного явления, — который можно обработать обычными методами математической статистики.

Нередко такой прием оказывается проще, чем попытки построить аналитическую модель явления и исследовать зависимость между его параметрами на этой модели. Для сложных операций, в которых участвует большое число элементов (машин, систем, людей, коллективов) и в которых случайные факторы сложным образом взаимодействуют между собой, метод статистических испытаний, как правило, оказывается проще аналитического.

В сущности, методом «розыгрыша» может быть решена любая вероятностная задача; однако оправданным он становится только в случае, когда процедура «розыгрыша» проще, а не сложнее применения аналитических, вычислительных методов.

Рассмотрим элементарный пример. Решается задача: по некоторой цели Ц производится четыре независимых выстрела, каждый из которых попадает в нее с вероятностью р = 0,5. Для поражения (уничтожения) цели одного попадания недостаточно, требуется не менее двух попаданий. Определить вероятность поражения цели.

Поставленную вероятностную задачу можно решить двумя способами: а) аналитически и б) «розыгрышем».

Сначала решим задачу аналитически. Вероятность поражения цели W вычислим через вероятность противоположного события - непоражения цели. Вероятность непоражения цели равна сумме вероятностей ни одного попадания и ровно одного попадания; вероятность ни одного попадания равна 0,5⁴; вероятность ровно одного попадания равна С₄¹·0,5¹·0,5³ = 4·0,5⁴, следовательно,

W = 1 - (0,5⁴ + 4·0,5⁴) ≈ 0,688.

Теперь попробуем решить ту же задачу «розыгрышем». Будем моделировать процедуру стрельбы с помощью другой, тоже случайной, процедуры. Вместо четырех выстрелов по цели будем бросать четыре монеты: появление герба будет условно означать «попадание», а решки — «промах». Если из четырех брошенных монет не менее двух упадут гербом, это будет значить, что цель «поражена». «Опытом» или «розыгрышем» в нашем случае будет бросание четырех монет; "результатом"или "исходом" этого опыта — "поражение" или «непоражение» цели.

Повторим такой «опыт», состоящий в бросании четырех монет, очень много раз подряд. Тогда, согласно теореме Бернулли, частота «поражения» цели почти наверняка будет мало отличаться от вероят­ности этого события W; значит, если мы бросим четыре монеты боль­шое число раз N и разделим число «поражений» цели на N, мы почти наверняка получим число, близкое к W, т. е. к 0,688.

В данном примере определение вероятности W розыгрышем было несравненно труднее, чем аналитическим расчетом. Однако далеко не всегда это бывает так. Очень часто оказывается, что получение вероятности события (или среднего значения случайной величины) аналитическим, расчетным путем настолько сложно и громоздко, что проще оказывается розыгрыш.

Тема 25. Имитационное моделирование. Метод Монте-Карло. Пример, иллюстрирующий метод.

Имитационное моделирование как статистический эксперимент.При решении задач анализа и синтеза СТС широко применяется имитационное моделирование. Этим термином называют исследование на ЭВМ, при котором показатели свойств СТС оценивают путем воспроизведения (имитации) процесса функционирования системы, учитывая адекватно реальные свойства системы и условия ее функционирования.

Следующие задачи решаются при синтезе СТС с помощью имитационныхмоделей наиболее часто:

· моделирование процесса функционирования исследуемой СТС для обоснования и проверки принятых технических решений, или для поиска новых технических решений;

· получение данных для разработки более простых моделей системы, в частности, эмпирической или регрессионной модели;

· проверка результатов, полученных на более простых моделях для обоснования допущений, принятых в этих моделях;

· получение результатов, заменяющих частично или полностью натурные испытания разрабатываемых образцов СТС или ее компонентов.

Имитационное моделирование можно трактовать как одну из разновидностей эксперимента с математической моделью системы. Характерной особенностью имитационного моделирования является большое внимание к подробностям функционирования системы, в том числе к случайным факторам (начальным условиям, погрешностям изготовления, возмущениям и т.д.), действующим в ней. Оно представляет собой развитие метода статистических испытаний (Монте-Карло) для изучения случайных процессов, имеющих место в сложных практических задачах.

Имитационное моделирование, подобно методу Монте-Карло, основано на использовании выборок для получения статистических оценок изучаемых величин, которые в данном случае выступают в качестве показателей свойств системы. Этот принцип предопределяет следующую организацию имитационного моделирования:

ü разрабатывается математическая модель и составляется программа для осуществления одного испытания системы и получения одной реализации случайного процесса в ней;

ü с использованием разработанной программы проводится эксперимент, т.е. вычисляется реализация случайного процесса в системе от начального до конечного момента;

ü для получения выборки реализаций эксперимент многократно повторяется;

ü данные, полученные при многократных испытаниях системы, обрабатываются с помощью методов математической статистики и определяются статистические характеристики выходных величин имитационной модели.

При разработке программ имитационного моделирования возникает ряд вопросов методического характера, таких как имитация случайных факторов на ЭВМ, моделирование работы системы при действии случайных факторов, алгоритмы статистической обработки результатов имитации и другие. Ответы на эти вопросы могут быть получены с помощью методов теории вероятностей и математической статистики. Первичным источником случайности при имитации случайных факторов на ЭВМ являются генераторы псевдослучайных чисел, равномерно распределенных на отрезке [0, 1], - специальные подпрограммы, имеющиеся в составе стандартного программного обеспечения ЭВМ или разрабатываемые самим разработчиком модели. Реализации всех других случайных факторов в системе получают путем преобразования этих чисел с помощью некоторого алгоритма, зависящего от типа имитируемого случайного фактора (событие, величина, процесс или поле) и его статистических характеристик. Например, реализации случайных величин с произвольным распределением вероятностей могут быть получены путем преобразования псевдослучайных чисел, распределенных равномерно на отрезке [0, 1], с помощью алгоритма, составленного с применением метода обратных функций или гистограммного метода, а реализации гауссовского случайного процесса — с помощью алгоритмов, основанных на использовании формирующего фильтра или канонического разложения.

Структура имитационной модели СТС и способ обработки результатов моделирования зависят от типа процесса в модели изучаемой системы (цепь, последовательность, дискретный или непрерывный процесс), от таких свойств этого процесса, как стационарность и эргодичность, а также оттого, в каком режиме — переходном или установившемся, требуется оценить показатели свойств СТС. В том случае, когда процесс в СТС — стационарный и эргодичный, а искомыми являются показатели свойств СТС в установившемся режиме ее функционирования, их можно рассчитать, обрабатываярезультаты моделирования одной достаточно длинной реализации процесса в СТС. При этом, чтобы исключить влияние переходного процесса, обработку реализации следует начинать, отступив от начала моделирования на интервал, превосходящий предполагаемое время переходного процесса в системе. Если же процесс в изучаемой системе — не эргодичный, или если показатели СТС требуется оценить в переходном режиме ее функционирования, то имитационное моделирование должно предусматривать имитацию и обработку многих реализаций процесса в системе.

При обработке результатов моделирования возникают и другие вопросы, относящиеся к математической статистике. Такими вопросами,в частности являются понижение дисперсий оценок показателей, применение способов съема измерений при моделировании с использованием эргодического свойства, с помощью которых достигается статистическая независимость измерений, и другие. Со способами решения различных вопросов применения математической статистики при имитационном моделировании можно познакомиться в специальной литературе.

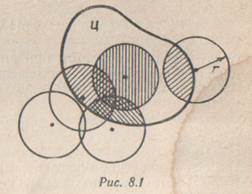
Рассмотрим пример такой задачи. Пусть производится бомбометание по некоторой цели Ц ( см. рис. 8.1).

Зона разрушительного действия бомбы имеет вид круга радиуса r.Сбрасывается п бомб. Для поражения цели (вывода ее из строя) нужно покрыть разру­шениями не менее k% площади цели. Требуется найти вероятность поражения цели W.

Несмотря на видимую простоту постановки задачи, ее аналитическое решение чрезвычайно сложно. Гораздо проще будет решить задачу «розыгрышем». Для этого надо будет «разыграть» координаты п точек попадания (как это сделать — будет рассказано в дальнейшем); вокруг каждой точки попадания описать круг радиуса r и подсчитать общую пораженную площадь цели (на рис. 8.1 она заштрихована). Если эта площадь оказалась больше k% площади цели, считать, что цель «поражена», если меньше k% — «не поражена». Такой «опыт», состоящий в «бросании» п бомб, нужно повторить очень много раз, отмечая каждый раз условным знаком (например, "+") опыт, в котором цель была «поражена». При большом числе «опытов» N вероятность поражения цели W может быть приближенно оценена как частота «поражения» цели:

где М — число «опытов», отмеченных плюсом.

Оказывается, что даже для рассмотренной нами сравнительно элементарной задачи процедура «розыгрыша» (получение вероятности методом Монте-Карло) будет значительно проще, чем нахождение той же вероятности аналитическим, расчетным методом. Пример является хорошим образцом типично «монте-карловской» задачи.

Заметим, что методом статистических испытаний (Монте-Карло) можно находить не только вероятности событий, но и средние значения (математические ожидания) случайных величин. При этом мы будем пользоваться уже не теоремой Бернулли, а законом больших чисел (теоремой Чебышева). Согласно этой теореме при большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины почти наверняка мало отличается от ее математического ожидания.

Так, если в условиях последнего примера (бомбометание по цели Ц) нам требуется найти не вероятность поражения, а математическое ожидание площади разрушений S_Р:

то его можно определить приближенно как среднее арифметическое площадей разрушений в большом числе N разыгранных «опытов":

где S_Рi— значение площади разрушений в i-м «опыте».

Аналогичным способом могут быть найдены не только математические ожидания, но и дисперсии интересующих нас случайных величин. Не забудем, что дисперсия случайной величины есть не что иное, как математическое ожидание квадрата центрированной случайной величины; оно может быть приближенно найдено как среднее арифметическое этих квадратов в отдельных «опытах». Так, в нашем примере дисперсия площади разрушений может быть приближенно найдена по формуле

или, что проще, через второй начальный момент:

Таким образом, метод Монте-Карло в исследовании операций есть метод математического моделирования случайных явлений, в котором сама случайность непосредственно включается в процесс моделирования и представляет собой его существенный элемент. Каждый раз, когда в ход операции вмешивается тот или другой случайный фактор, его влияние имитируется с помощью специально организованного «розыгрыша» или «жребия». Таким образом, строится одна реализация случайного явления, представляющая собой как бы результат одного «опыта». При большом числе реализаций интересующие нас характеристики случайного явления (вероятности, математические ожидания) находятся так же, как они находятся из опыта: вероятности — как частоты событий, математические ожидания — как средние арифметические значений соответствующих случайных величин.

Большое число реализаций, требующееся при применении метода Монте-Карло, делает его вообще громоздким и трудоемким. Прежде чем пускать в ход метод Монте-Карло, всегда имеет смысл попытаться решить задачу аналитически, и только если это не удается, прибегать к статистическому моделированию. Полезным оказывается хотя бы приближенное предварительное аналитическое решение задачи — это помогает выявить основные факторы, от которых зависит результат, и наметить план дальнейшей работы.

Моделирование случайных явлений методом Монте-Карло часто производится с целью проверить правомочность в данном случае того или другого математического аппарата, всегда основанного на некоторых допущениях. Пусть, например, рассматривая систему массового обслуживания, мы приближенно заменили не-пуассоновский поток заявок пуассоновским и непоказательное время обслуживания — показательным. Моделирование того же процесса методом Монте-Карло покажет, допустимы ли эти упрощения, к каким ошибкам они приводят, и позволит ввести соответствующие поправки.

Не нашли, что искали? Воспользуйтесь поиском по сайту: