|
|
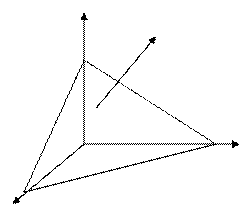
Глава II. Аналитическая геометрия на плоскости и в пространстве.§1. Декартова система координат. Определение 1. Три взаимно перпендикулярные числовые оси, имеющие общее начало отсчета и одинаковые масштабы, называются декартовой системой координат данного пространства. Координатные оси обычно обозначают буквами x, y и z или символами OX, OY и OZ . Любая точка М пространства находится во взаимно однозначном соответствии с множеством упорядоченных троек действительных чисел – координатами своих ортогональных проекций на осях х, у и z, называемых координатами самой точки М: М(Мх,Му,Мz). В качестве базиса векторного пространства выбираются орты i, j и k, сонаправленные координатным осям x, y и z соответственно (рис.12). Рассмотрим вектор Вектор с началом в точке О и концом в точке М называется радиус −вектором точки М. Пусть его координаты в данном базисе равны rx,ry и rz , т.е.
z Из определения суммы векторов (§2) сразу следует, что вектор Mz из слагаемых правой части равно проекции вектора r на М координатную ось (§3), умноженную на соответствующий kr базисный орт: О j My y i вектора по базису (§4, Т1) имеем следующий результат: Мх x рис.1 В декартовой системе координат координаты вектора в ортонормированном базисе равны его проекциям на координатные оси.
§2.Простейшие задачи аналитической геометрии. В этом параграфе будут рассмотрены три задачи: вычисление координат вектора 1. Вычисление координат вектора
М и В' с координатами Ах и Вх − проекции точек А и В на ось ОХ. А Координаты вектора равны его проекциям на координатные оси (§1). Следовательно, его первая координата равна Вх − Ах (гл.I ,§3,св.3). А' М' В' ОХ Аналогичный результат получается для остальных координатных Рис.2 осей. Таким образом: 2. Вычисление длины отрезка. Так как длина отрезка АВ (|AB|) равна (гл.1, §7). 3. Деление отрезка в данном отношении. Рассмотрим т. направленный отрезок
Замечания. 1. Наиболее важным частным случаем является деление отрезка пополам:
2. Полученный результат сохраняется для любого расположения точек, лежащих на одной прямой. В случае, когда т. §2. Аналитическая геометрия на плоскости. В этом и нескольких последующих параграфах будут рассмотрены основные задачи аналитической геометрии на плоскости. Пусть дана некоторая фиксированная координатная плоскость, т.е. плоскость, на которой задана декартова система координат XOY и ортонормированный базис {i, j}, орты которого сонаправлены координатным осям х и у соответственно. Любая точка плоскости определяется двумя координатами – координатами своих ортогональных проекций на эти оси: М(х, у). Любой вектор плоскости так же определяется двумя координатами – коэффициентами разложения по базису или, что то же самое, своими проекциями на координатные оси: а = (ах , ау). Линия на плоскости определяется как геометрическое место точек плоскости (гмт), удовлетворяющих некоторому геометрическому или аналитическому условию. Геометрическое условие необходимо перевести в аналитическое (геометрия – аналитическая!), а у аналитического − выяснить геометрический смысл (аналитическая геометрия). Аналитическим заданием линии является уравнение с двумя переменными: F(x, y) = 0, т.е. линия на плоскости определяется как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению. Иногда линия задается в параметрической форме: Замечание. В математическом анализе уравнение F(x, y) = 0 называют неявным заданием функции (частный случай y = f (x) называется явным заданием), т.е. используются понятия функции и аргумента. В аналитической геометрии, вообще говоря, переменные х и у считают равноправными.
§3. Прямая на плоскости. Определим прямую l на плоскости следующим образом: Пусть заданы произвольная фиксированная т. М0(х0,у0) ненулевой вектор нормальным вектором прямой или просто нормалью. Прямой, проходящей через т. М0 , с данным нормальным вектором Используя данное определение, легко написать аналитическое задание или уравнение этой прямой.
М0 М х Итак, Рис.3 через точку (х0,у0) и перпендикулярной вектору Если обозначить выражение − Ах0 − Ву0 через С , то получим общее уравнение прямой на плоскости:
§4.Специальные виды уравнения прямой. I. Уравнение с угловым коэффициентом. Хорошо известное уравнение y = k x + b, где k = tgφ − тангенс угла наклона прямой к оси ОХ , а b − величина отрезка от начала координат до точки пересечения прямой с осью OY . II. Уравнение прямой, проходящей через две заданные точки. Так как прямая полностью определяется двумя точками, естественно написать соответствующее уравнение. Пусть даны две различные точки, принадлежащие прямой l:
III. Каноническое и параметрические уравнения прямой. Любой вектор, коллинеарный прямой l называется направляющим вектором прямой. (В частности, вектор прямой и направляющий вектор
к параметру t , то получим параметрические уравнения прямой: IV. Уравнение прямой в отрезках. Пусть известны точки пересечения прямой с осями координат: Отсюда :
§5.Основные задачи, связанные с прямой. I. Угол между прямыми. Рассмотрим две прямые l1 и l2 . Если эти прямые заданы своими общими уравнениями, то косинус угла между ними может быть найден как косинус угла между их нормалями или направляющими векторами с помощью скалярного произведения: Замечание. Направляющий вектор из нормального (и наоборот) легко получить следующим образом: В случае задания прямых уравнениями с угловым коэффициентом, имеем соотношение:
II. Условия параллельности и ортогональности двух прямых.
III. Расстояние от точки до прямой. Вычислим расстояние от произвольной точки плоскости M*(x*, y*) до прямой l: Ax+By+C = 0.
•М* вектора М Т.к. точка Рис.4 Замечание. Знак выражения Ах*+Ву*+С меняется при переходе точки через прямую.
§6. Алгебраические линии на плоскости. Линии, описываемые алгебраическим уравнением n −го порядка от двух переменных, называют линиями или кривыми n −го порядка на плоскости. Линии 1 – го порядка описываются уравнением Ах + Ву + С = 0 ( Уравнения 2 – го порядка : кривыми 2 – го порядка и представляют собой целое семейство плоских кривых.
§7.Окружность. Определение. Окружность − геометрическое место точекплоскости, равноудаленных от заданной фиксированной точки плоскости, называемой центром окружности. Расстояние от точек окружности до центра – радиус окружности. Если центр окружности находится в т. М0(х0,у0), а радиус равен r, то уравнение окружности может быть написано в следующем виде:
§8.Эллипс. Определение.Эллипсом называется геометрическое место точекплоскости, сумма расстояний от каждой из которых до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Для вывода уравнения эллипса выберем фокусы в точках F1(-c,0) и F2(c,0) (c > 0) , а сумму расстояний обозначим через 2а (2a >2 c). Пусть М(х,у) – произвольная точка эллипса. Тогда:
b М −a F1 F2 a x Обозначив a2 − c2 = b2 , окончательно −b получим:
рис.5 Числа a и b называются полуосями эллипса (точки пересечения эллипса с осями координат имеют своими координатами числа Отношение расстояния между фокусами эллипса к длине большой оси называется эксцентриситетом эллипса: эллипса. При ε = 0 эллипс превращается в окружность, при ε = 1 − вырождается в отрезок. Написанное выше уравнение называется каноническим уравнением эллипса. (Вообще, в геометрии словами каноническое уравнение, обычно, называют уравнение, содержащее в явном виде все основные геометрические характеристики объекта. См. например, каноническое уравнение прямой (§4)) Это уравнение является частным случаем уравнения 2 – го порядка (§6). Нетрудно видеть, что любое уравнение AC > 0. (Более общие условия будут выведены позже) Пример. с центром в т.(−1,2) и полуосями 2 и 4. Замечания. 1) Фокусы эллипса всегда расположены на больших полуосях . 2) Если правая часть = 0, то вырожденный эллипс (точка), если = −1 – мнимый эллипс. §9.Гипербола. Определение.Гиперболой называется геометрическое место точекплоскости, разность расстояний от каждой из которых до двух фиксированных точек плоскости, называемых фокусами гиперболы, есть величина постоянная и не равная нулю. Снова выберем фокусы в точках F1(-c,0) и F2(c,0) (c > 0) , а модуль разности расстояний обозначим через 2а (2a < 2 c). Для произвольной точки гиперболы М(х,у) имеем:
После проведения элементарных преобразований, аналогичных предыдущим, получим каноническое уравнение гиперболы: b При а F2 x Эксцентриситет гиперболы определяется так же, как и у эллипса, и равен рис.6 Замечания. 1) При исследовании уравнения 2 – го порядка могут быть получены уравнения следующего вида: −1 в правой части означает, что гипербола повернута вокруг начала координат на 900 . 2) Уравнение 3) «Школьное» уравнение гиперболы гиперболы повернута на 450, а асимптотами являются координатные оси. Пример. Определить вид и характеристики кривой:
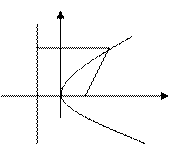
§10.Парабола. Определение.Параболой называется геометрическое место точекплоскости, расстояние от каждой из которых до фиксированной точки плоскости, называемой фокусом параболы,равно расстоянию до фиксированной прямой, называемой директрисой параболы.
у Пусть фокус имеет координаты (p/2,0): F(p/2,0), а директриса записывается уравнением х = −р/2. Расстояние между фокусом •M(x,y) и директрисой равно р − параметру параболы (рис.7). Точки параболы удовлетворяют уравнению: −р/2 F х После простых преобразований получим каноническое уравнение параболы: у2 = 2рх. Рис.7 §11.Кривые второго порядка – заключение. В предыдущих параграфах были рассмотрены три вида кривых второго порядка: эллипсы, гиперболы и параболы, а также их частные и вырожденные случаи. Два первых вида называют центральными кривыми. Параболы – не центральные. Можно доказать (это будет сделано позже), что этими тремя видами исчерпываются все кривые второго порядка. Из примера §8 видно, что слагаемые 1 – ой степени в уравнении кривой (§6) влияют только на параллельный перенос кривых. В дальнейшем будет доказано, что слагаемое 2Вху определяет поворот кривой вокруг начала координат. §12. Аналитическая геометрия в пространстве. Поверхности в пространстве задаются либо уравнением с тремя переменными: либо в параметрической форме: Линии в пространстве задаются пересечением двух поверхностей, или параметрически: т.е. При решении задач в пространстве особенно важно знать геометрический смысл параметров, входящих в уравнения.
§13.Плоскость в пространстве. Определение. Плоскостью называется геометрическое место концов векторов, имеющих общее начало и ортогональных данному ненулевому вектору, называемому нормальным вектором плоскости. Для вывода уравнения плоскости Р зафиксируем т.
т. Если раскрыть скобки и обозначить Замечание. И в общем уравнение плоскости коэффициенты А, В и С являются координатами вектора нормали.
§14.Специальные случаи уравнения плоскости. I. Уравнение плоскости, проходящей через три точки. Пусть тт.
II. Уравнение плоскости в отрезках. Возьмем в качестве предыдущих точек точки пересечения с осями координат:
c Уравнение плоскости примет вид: • М0 b y
a х рис.8
§15. Основные задачи, связанные с плоскостью. I. Условия параллельности, перпендикулярности, угол между плоскостями. Даны две плоскости: Все перечисленные условия следуют из геометрического смысла коэффициентов (§13).
II. Расстояние от точки до плоскости. Вычисляется так же, как в случае прямой на плоскости (§5). Пусть После простых преобразований получим (#) III. Связка и пучок плоскостей. Определение1. Множество плоскостей, проходящих через единственную общую точку М0 , называется связкой плоскостей с центром в т. М0 ( Обозначение − S(M0)). Рассмотрим три плоскости, принадлежащие S(M0):
Теорема. Уравнение {Нужно доказать 2 утверждения: 1) 1) Так как все слагаемые Q равны нулю в т. М0 , то и Q = 0 в этой точке. 2) Так как СЛАУ (*) имеет единственное решение (x0,y0,z0), то из правила Крамера следует, что определитель системы отличен от нуля, т.е. векторы
Определение2. . Множество плоскостей, проходящих через общую прямую – ось плоскостей, называетсяпучком плоскостей. Теорема.Уравнение пучка плоскостей имеет вид:
§16. Прямая в пространстве. Наиболее простым заданием прямой в пространстве является ее задание, как линии пересечения двух плоскостей: (Естественно предполагать, что плоскости не совпадают и не параллельны) Однако, такое задание имеет большой недостаток: оно не содержит в явном виде ни одной геометрической характеристики прямой. Удобнее пользоваться каноническим уравнением прямой, в котором она определяется как геометрическое место концов векторов, имеющих общее начало и коллинеарных данному ненулевому вектору − направляющему вектору прямой. Если обозначить любую фиксированную точку прямой через М0 , а направляющий вектор
Замечание. На самом деле, каноническое уравнение представляет собой систему двух линейных уравнений с тремя переменными, т.е. линию пересечения двух плоскостей. Но, во – первых, это особые плоскости (параллельные координатным осям) и, во – вторых, в записи системы геометрические характеристики прямой фигурируют в явном виде. Пример. Перейти к каноническому заданию: {Положим z = 0. Тогда x =2, y = − 1; От канонического уравнения легко перейти к параметрическому заданию. Приравняем полученную пропорцию к новой переменной и выразим через нее переменные x, y и z:
Пример. Найти точку пересечения прямой {x = 1 + 2t, y = −3t, z = −2 + t → 7t − 14 = 0 → t = 2 → (5, −6, 0) } Уравнение прямой через две точки можно написать, взяв в качестве направляющего вектора вектор (#) В некоторых задачах удобно пользоваться векторным представлением прямой. В этом случае прямая задается радиус – вектором (§1) текущей точки прямой.
Здесь :
M0 l = (p, q, r) − направляющий вектор прямой.
рис.9
§17.Основные задачи. Две задачи, связанные с прямой были уже рассмотрены на примерах в предыдущем параграфе. Задачи, связанные с вычислением углов между прямыми, прямой и плоскостью, включая условия ортогональности и параллельности, решаются с использованием направляющих векторов прямых и нормальных векторов плоскостей. Так, например, синус угла между прямой и плоскостью будет равен модулю косинусу угла между соответствующими направляющим и нормальным векторами:
Условия ортогональности и параллельности прямой и плоскости записываются следующим образом: Рассмотрим две прямые с направляющими векторами
деленный на площадь основания. Пример. Как расположены прямые Если они пересекаются – найти общую точку. Если нет – расстояние между ними. {
§18.Поверхности в пространстве. Общая постановка задач в пространстве была дана в §12. Рассмотрим сейчас несколько специальных задач. I. Цилиндрические поверхности. Рассмотрим уравнение с двумя переменными в пространстве : F(x,y) = 0. На плоскости XOY оно описывает некоторую кривую. В пространстве каждой точке (x*,y*) этой кривой будет соответствовать прямая Аналогично рассматриваются цилиндры, образующие которых параллельны другим координатным осям: F(x, z) = 0 и F(y, z) = 0. Замечание. Естественно, существуют наклонные цилиндры, в уравнения которых входят все переменные в явном виде. Однако, должен существовать такой поворот системы координат, после которого одна из переменных будет отсутствовать в записи уравнения. Примеры. 1) 2) 3) у2 = 8z − параболический цилиндр с образующей, параллельной оси OХ.
§19. Поверхность вращения. В этом параграфе будут рассмотрены поверхности, образованные вращением плоской кривой вокруг одной из координатных осей. Для определенности, возьмем кривую F(y, z) = 0 в плоскости YOZ и ось вращения ОZ . Зафиксируем произвольное значение z* и выразим из уравнения F(y, z*) = 0 соответствующее значение у = f(z*). При вращении, в плоскости z = z* получится окружность x2 + y2 = f 2(z*). Уравнение самой поверхности вращения будет иметь вид x2 + y2 = f 2(z) (рис.10).
z F(y, z*) = 0 относительно у совсем не обязательно, тем более, F(y, z) = 0 что оно может быть достаточно трудоемким, либо невозможным. Поэтому, уравнение поверхности вращения в данном случае записывается следующим образом: y
x рис.10 Правило записи уравнения поверхности вращения плоской кривой вокруг координатной оси: Поверхность вращения плоской кривой вокруг координатной оси может быть получена заменой второй переменной в уравнении кривой на квадратный корень из суммы квадратов этой и отсутствующей переменных (в рассмотренном случае Пример. Написать уравнения поверхностей, полученных в результате вращения кривой у2 = 6х вокруг осей ОХ и OY. {
Замечание. Если в уравнении некоторой поверхности две переменные присутствуют только в связке как сумма квадратов, то эта поверхность является поверхностью вращения вокруг координатной оси третьей переменной.
§20.Проекция линии пересечения двух поверхностей на координатную плоскость. Одной из важнейших задач исследования взаимного расположения двух поверхностей является определение линии их пересечения. Формально, линия пересечения записывается как система двух уравнений с тремя переменными (см. §12 и §16): значение z*, при котором точка (x*,y*, z*) принадлежит линии пересечения поверхностей. Следовательно, прямая параллельная оси OZ, проходящая через точку линии пересечения поверхностей, на плоскости XOY пересекает кривую f(x,y) = 0. Множество таких прямых образуют цилиндр с направляющей f(x,y) = 0 в плоскости XOY и образующей параллельной оси OZ (§18). Таким образом, доказано следующее утверждение: Если исключить одну из переменных из уравнений двух поверхностей, то получится уравнениепроекции линии пересечения этих поверхностей на координатную плоскость двух оставшихся переменных. Пример. Найти проекцию линии пересечения поверхностей плоскость YOZ. {Исключим х:
§21. Поверхности второго порядка. Исследование методом сечений. Общий вид алгебраической поверхности второго порядка представляет собой многочлен второй степени относительно трех переменных:
Одним из наиболее продуктивных методов изучения поверхностей в пространстве является метод сечений. Он заключается в исследовании кривых, получающихся в сечениях поверхности плоскостями, параллельными координатным. Для этого достаточно зафиксировать одну из переменных в уравнении поверхности и получить, тем самым, уравнение кривой в плоскости, параллельной двум другим координатным осям. Этот метод будет использован в последующих параграфах при исследовании поверхностей второго порядка. При этом будут рассматриваться только уравнения, непосредственно сводящиеся к каноническим.
§22.Эллипсоид. Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением При этих условиях уравнение эллипсоида может быть написано в каноническом виде:
Для определения формы эллипсоида применим метод сечений. Пусть z = h фиксировано.
1) 2) Наибольшие полуоси эллипс будет иметь при h = 0. 3) Аналогичная картина будет иметь место в сечениях x = h или y = h. (рис.11) рис.11
Как и в случае эллипса, числа a, b и c называются полуосями эллипсоида. Если они все разные, то эллипсоид называется трехосным. Если две полуоси равны друг другу, то мы получим эллипсоид вращения (§19). В случае равенства всех полуосей – имеем сферу:
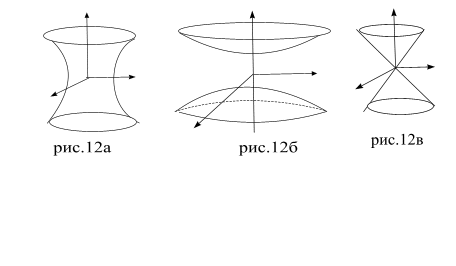
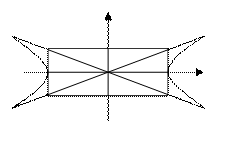
§23.Гиперболоиды и конус. Гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением С – меньше нуля: A > 0, B > 0, C < 0. В зависимости от знака L имеем два типа гиперболоидов. I. L < 0. После стандартных преобразований (§22) получим уравнение: Снова воспользуемся методом сечений. Плоскости z = h поверхность пересекает по эллипсам С увеличением h ( или z) полуоси эллипса увеличиваются. Минимальные полуоси будут при h = 0 , т.е. в плоскости ХОY.
В плоскостях x = h (или y = h ) получаются гиперболы

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.

 . В свою очередь, каждое
. В свою очередь, каждое и
и . В силу единственности разложения
. В силу единственности разложения по координатам точек А и В, вычисление длины отрезка и деление отрезка в данном отношении.
по координатам точек А и В, вычисление длины отрезка и деление отрезка в данном отношении. В Пусть
В Пусть 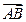 − произвольный вектор пространства (рис.2). Точки А'
− произвольный вектор пространства (рис.2). Точки А' .
. , то |AB| =
, то |AB| = 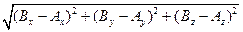
 (рис.2). Требуется определить число
(рис.2). Требуется определить число  , где АМ и МВ − величины направленных отрезков
, где АМ и МВ − величины направленных отрезков  , называемое отношением, в котором т. М делит
, называемое отношением, в котором т. М делит . Из курса элементарной геометрии и полученных результатов имеем:
. Из курса элементарной геометрии и полученных результатов имеем: 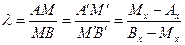 . Отсюда легко получаем координаты точки М:
. Отсюда легко получаем координаты точки М: .
.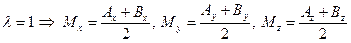
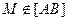 величина λ будет отрицательной.
величина λ будет отрицательной.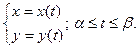
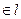 и произвольный фиксированный
и произвольный фиксированный , перпендикулярный данной прямой, который называется
, перпендикулярный данной прямой, который называется называется геометрическое место концов векторов на плоскости, имеющих начало в т. М0 и ортогональных вектору
называется геометрическое место концов векторов на плоскости, имеющих начало в т. М0 и ортогональных вектору 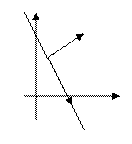 у Пусть т. М(х,у) − произвольная точка прямой.
у Пусть т. М(х,у) − произвольная точка прямой.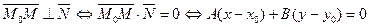
 − уравнение прямой, проходящей
− уравнение прямой, проходящей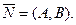
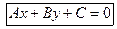
 . В этом случае
. В этом случае  . Отсюда :
. Отсюда : − уравнение прямой через две точки.
− уравнение прямой через две точки. (пункт II) − направляющий) Если дана точка на
(пункт II) − направляющий) Если дана точка на , то последнее уравнение можно переписать в виде:
, то последнее уравнение можно переписать в виде: − каноническое уравнения прямой. Если полученную пропорцию приравнять
− каноническое уравнения прямой. Если полученную пропорцию приравнять .
. .
. уравнение прямой в отрезках.
уравнение прямой в отрезках. .
.


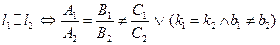
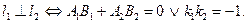
 Пусть М(х,у) − произвольная точка прямой,
Пусть М(х,у) − произвольная точка прямой,  на вектор нормали:
на вектор нормали: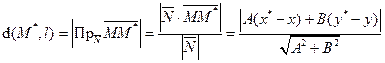
 , то Ах + Ву = − С и окончательно получаем:
, то Ах + Ву = − С и окончательно получаем: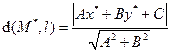
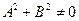 ) представляют собой прямые.
) представляют собой прямые. ,(
,(  ) называют
) называют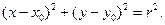
 y
y 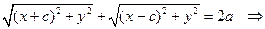
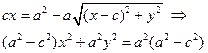
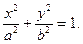
 а и
а и 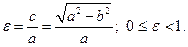 Эксцентриситет характеризует форму
Эксцентриситет характеризует форму представляет собой эллипс при условии
представляет собой эллипс при условии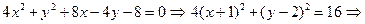
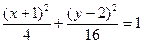 − эллипс
− эллипс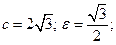 F1(−1,
F1(−1,  ) и F2(−1,
) и F2(−1,  ).
).
 y Из уравнения сразу следует, что
y Из уравнения сразу следует, что 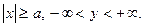
 гипербола имеет асимптоты
гипербола имеет асимптоты  .
.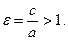
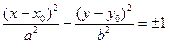 Центр таких гипербол находится в точке (х0,у0), а
Центр таких гипербол находится в точке (х0,у0), а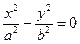 описывает две пересекающиеся прямые.
описывает две пересекающиеся прямые.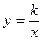 представляет собой частный случай, когда ось
представляет собой частный случай, когда ось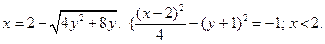
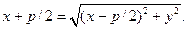
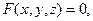
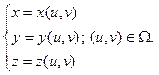
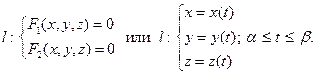
 и нормальный вектор
и нормальный вектор (рис.8).Тогда
(рис.8).Тогда  . Отсюда получаем:
. Отсюда получаем: − уравнение плоскости, проходящей через
− уравнение плоскости, проходящей через и ортогональной вектору
и ортогональной вектору  .
. , то получим общее уравнение плоскости:
, то получим общее уравнение плоскости: 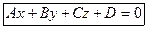
 Необходимым и достаточным условием принадлежности т. М той же плоскости является компланарность векторов
Необходимым и достаточным условием принадлежности т. М той же плоскости является компланарность векторов  В свою очередь, условие компланарности (гл.I,§11,св.2) приводит к следующему уравнению:
В свою очередь, условие компланарности (гл.I,§11,св.2) приводит к следующему уравнению: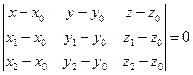
 z
z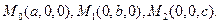



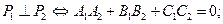
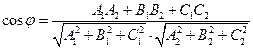
 произвольная точка пространства. Расстояние от точки до плоскости равно модулю проекции
произвольная точка пространства. Расстояние от точки до плоскости равно модулю проекции 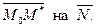
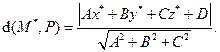
 ……………………..(*)
……………………..(*)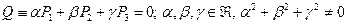 описывает связку плоскостей с центром в данной точке.
описывает связку плоскостей с центром в данной точке. 2)
2)  .
. линейно независимы и
линейно независимы и . Значение D = D* , т.к. все плоскости проходят через т. М0 }
. Значение D = D* , т.к. все плоскости проходят через т. М0 } ,приусловии
,приусловии 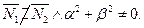
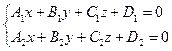 .
. , то для произвольной точки прямой М получим соотношение:
, то для произвольной точки прямой М получим соотношение: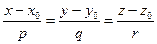 − каноническое уравнение прямой в пространстве. (См. §4,п.III)
− каноническое уравнение прямой в пространстве. (См. §4,п.III)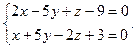
 . Отсюда:
. Отсюда:  }
}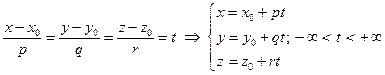
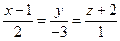 с плоскостью x – y +2z – 11 = 0.
с плоскостью x – y +2z – 11 = 0. :
: 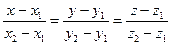

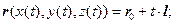 (рис.9)
(рис.9) M r0 − радиус – вектор т. М0
M r0 − радиус – вектор т. М0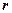
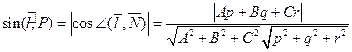
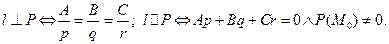
 и проходящие через точки М1 и М2 соответственно. Прямые могут пересекаться, быть параллельными или скрещиваться. В двух первых случаях смешанное произведение
и проходящие через точки М1 и М2 соответственно. Прямые могут пересекаться, быть параллельными или скрещиваться. В двух первых случаях смешанное произведение 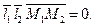 Если же прямые скрещиваются, то
Если же прямые скрещиваются, то Оба условия являются необходимыми и достаточными. Так как расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат, то оно может быть найдено по формуле
Оба условия являются необходимыми и достаточными. Так как расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат, то оно может быть найдено по формуле  − объем параллелепипеда
− объем параллелепипеда и
и  ?
?
 прямые скрещиваются.
прямые скрещиваются.
 }
} , т.е. прямая, проходящая через точку (x*,y*,0) и параллельная оси OZ. Поверхность, образованная множеством всех таких прямых, называется цилиндром с направляющей F(x,y) = 0 в плоскости XOY и образующей параллельной оси OZ.
, т.е. прямая, проходящая через точку (x*,y*,0) и параллельная оси OZ. Поверхность, образованная множеством всех таких прямых, называется цилиндром с направляющей F(x,y) = 0 в плоскости XOY и образующей параллельной оси OZ. − прямой круговой цилиндр радиуса r и осью OZ.
− прямой круговой цилиндр радиуса r и осью OZ.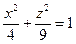 − эллиптический цилиндр с образующей, параллельной оси OY.
− эллиптический цилиндр с образующей, параллельной оси OY. Необходимо отметить, что аналитическое решение уравнения
Необходимо отметить, что аналитическое решение уравнения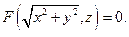
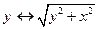 ).
).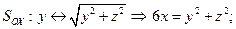
 }
} . Для анализа линии пересечения исключим в данной системе одну из переменных, например z. В результате получится одно уравнение с двумя неизвестными: f(x,y) = 0, которое можно воспринимать как кривую на плоскости XOY. Любой точке этой кривой (x*,y*) , будет соответствовать некоторое
. Для анализа линии пересечения исключим в данной системе одну из переменных, например z. В результате получится одно уравнение с двумя неизвестными: f(x,y) = 0, которое можно воспринимать как кривую на плоскости XOY. Любой точке этой кривой (x*,y*) , будет соответствовать некоторое и
и 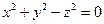 на
на гипербола. Из уравнения первой поверхности (круговой цилиндр) следует, что
гипербола. Из уравнения первой поверхности (круговой цилиндр) следует, что 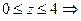 верхняя ветвь,
верхняя ветвь,  }
}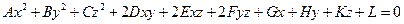
 , коэффициенты А, В и С − числа одного знака, а L имеет знак им противоположный.
, коэффициенты А, В и С − числа одного знака, а L имеет знак им противоположный.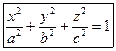 где
где  .
. Сечение эллипсоида плоскостью z = h будет иметь вид
Сечение эллипсоида плоскостью z = h будет иметь вид  − эллипс с данными полуосями. Отсюда следуют несколько выводов:
− эллипс с данными полуосями. Отсюда следуют несколько выводов: ; при h = c эллипс вырождается в точку.
; при h = c эллипс вырождается в точку.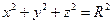 .
. .
. .
. . (рис.12а)
. (рис.12а)