|
|
Свойства линейных операций.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Глава I. Векторная алгебра. §1. Векторы в пространстве. Основные определения. Определение 1. Вектором в пространстве называется направленный отрезок. Таким образом, векторы в отличие от скалярных величин имеют две характеристики: длину и направление. Будем обозначать векторы символами (Здесь А и В – начало и конец данного вектора Длина вектора обозначается символом модуля: Различают три вида векторов, задаваемых отношением равенства между ними:
В курсе аналитической геометрии рассматриваются только свободные векторы. Определение 2. Вектор, длина которого равна нулю, называется нулевым вектором, или ноль – вектором. Очевидно, начало и конец нулевого вектора совпадают. Нулевой вектор не имеет определенного направления или имеет любое направление. Определение 3. Два вектора, лежащих на одной прямой или параллельных прямых называются
b Нулевой вектор можно считать коллинеарным любому. рис.2 Определение 4.Два коллинеарных и одинаково направленных вектора называются сонаправленными. Обозначают: Теперь можно дать строгое определение равенства свободных векторов: Определение 5.Два свободных вектора называются равными, если они сонаправлены и имеют одинаковую длину. Определение 6.Три вектора, лежащих в одной или параллельных плоскостях называются компланарными. Два перпендикулярных вектора называют взаимно ортогональными: Нулевой вектор можно считать ортогональным любому. Определение 7.Вектор единичной длины называется единичным вектором или ортом. Орт, сонаправленный ненулевому вектору а называют ортом вектора а : ea .
§2. Линейные операции над векторами. На множестве векторов определены линейные операции: сложение векторов и умножение вектора на число. I. Сложение векторов. Суммой 2 – х векторов называется вектор, начало которого совпадает с началом первого, а конец с концом второго, при условии, что начало второго совпадает с концом первого.
таким образом (рис.3а), совпадает с суммой векторов, построенной по правилу параллелограмма (рис.6). b Однако, данное правило позволяет строить a сумму любого числа векторов (рис.3б). a+b рис.3а
b a+b+c рис.3б c Произведением вектора а на число длина которого равна и противоположно направленный при λ < 0. рис.4 Вычитание векторов определяется как действие обратное сложению: Определение.Разностью векторов а и b называется такой вектор c = a − b, который при сложении с вектором b дает вектор a : b + c = a (рис.5).
ba−b начала векторов a и b в общую точку. Очевидно следующее равенство: a + (−1)a = a − a = 0. a (Строгоедоказательство предоставляется читателям) рис.5 Замечание. Ноль в правой части последнего равенства есть нулевой вектор, а не число. Равенство (−1)b = −b дает еще один способ построения разности векторов: а−b = a+(−b). Т.е. при вычислении разности можно у вычитаемого вектора изменить направление на противоположное и построить сумму полученных векторов. Свойства линейных операций. 1. Переместительное свойство сложения (коммутативность). a + b = b + a. {рис.6} 2. Сочетательное свойство сложения (ассоциативность). (a + b) + c = a + (b + c). {рис.7} 3. Дистрибутивность умножения а) (λ+μ)а = λа + μа. {Очевидно} б) λ(a+b) = λa + λb. {Следует из подобия (рис.8)} 4. λ(μа) = (λμ)а . {Очевидно }
b b a+b = b+a b+c λb λ(a+b) a+bb a (a+b)+c=a+(b+c) a+b aa λa рис.6 рис.7 рис.8
§3.Проекция вектора на ось. Определение 1. Осью называется прямая, на которой задано положительное направление. Числовой осью называют ось, на которой заданы начало отсчета и масштаб (единичный отрезок). Все точки числовой оси находятся во взаимно – однозначном соответствии с множеством действительных чисел. Началу отсчета, естественно, ставится в соответствие число 0. Соответствующие точкам числа являются координатами точек относительно этой числовой оси. Рассматривая некоторую ось u (не числовую), будем предполагать (по умолчанию) наличие единого масштаба во всем пространстве, содержащем эту ось.
А' В' и рис.9 Основные свойства величин отрезков(будем считать, что тт. А, В и С лежат на оси и ):
{При расположении точек в указанном порядке по направлению оси − равенство очевидно. Пусть точки расположены иначе, например: В, С, А → ВА = ВС + СА → −АВ = ВС −АС → АС = АВ + ВС. Остальные случаи доказываются аналогично}
АВ = Ви − Аи . {Очевидно} Рассмотрим теперь произвольный вектор Определение 3.Ортогональной проекцией вектора При Из определения сразу следует, что проекция вектора на ось есть число. Если начало вектора поместить на ось и угол между вектором и осью обозначить через φ, то для вычисления проекции имеем очевидное соотношение: При Замечание. Можно рассматривать и не ортогональные проекции вектора на ось. Для этого следует провести из концов вектора параллельные прямые, не перпендикулярные оси до пересечения с ней. Все основные свойства ортогональных проекций будут выполняться. Однако, в дальнейшем, по умолчанию, все проекции мы будем считать ортогональными. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
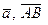, или а.
(рис.1)) а В 
. А рис.1
коллинеарными (рис.2). Обозначают: 
. a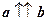
. 
.
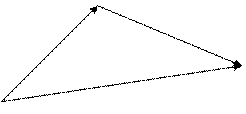Легко видеть, что сумма двух векторов, определенная
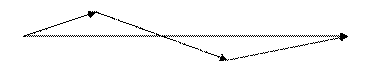a
II. Умножение вектора на число.
называется вектор, a
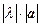, сонаправленный вектору а при λ > 0 -0.7a
Из рис.5 следует, что строить вектор разности удобнее, поместив
c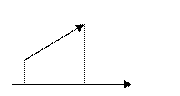
Определение 2.Величиной отрезка [АВ] 
(обозначается АВ) называется число, равное длине этого отрезка и взятое со знаком «+», если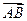 
направлен по оси и со знаком «−», если − против, т.е. 
. 
При этом необходимо учитывать, что угол φ отсчитывается от оси в положительном направлении, т.е. против часовой стрелки. Если еи − орт, сонаправленный оси и, то в частном случае 
.