Метод элементарных преобразований
Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Метод окаймляющих миноров
Пусть в матрице  найден ненулевой минор найден ненулевой минор 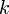 -го порядка -го порядка  . Рассмотрим все миноры . Рассмотрим все миноры  -го порядка, включающие в себя (окаймляющие) минор -го порядка, включающие в себя (окаймляющие) минор  ; если все они равны нулю, то ранг матрицы равен ; если все они равны нулю, то ранг матрицы равен 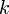 . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется. . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.
9-ый вопрос
В линейной алгебре матрица считается матрицей ступенчатого вида по строкам если
· все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
· ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Вот пример матрицы ступенчатого вида по строкам:

Метод Гаусса приведения матрицы к ступенчатому виду
Элементарными преобразованиями матрицы называются следующие ее преобразования:
I. Перестановка двух столбцов (строк) матрицы.II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.
Матрица  , полученная из исходной матрицы , полученная из исходной матрицы 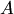 конечным числом элементарных преобразований, называется эквивалентной. Это обозначается конечным числом элементарных преобразований, называется эквивалентной. Это обозначается  . .
10-ый вопрос (1-ая часть)
Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA ≠ 0 .
11-ый вопрос
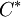 (союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц. (союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
 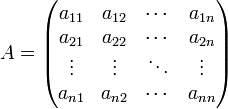 Где: Где:
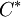 — присоединённая(союзная, взаимная) матрица; — присоединённая(союзная, взаимная) матрица;  — алгебраические дополнения исходной матрицы; — алгебраические дополнения исходной матрицы;  — элементы исходной матрицы. — элементы исходной матрицы.
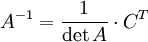
Теорема 4.1. (необходимое и достаточное условие существования обратной матрицы). Обратная матрица A  существует тогда и только тогда, когда исходная матрицаАневырожденная. существует тогда и только тогда, когда исходная матрицаАневырожденная.
Доказательство. Необходимость. Пусть матрица А имеет обратную A  , т. е. A , т. е. A  A A  AA AA   E. По свойству 10 определителей имеем D(A E. По свойству 10 определителей имеем D(A  A) A)  = D(A = D(A  )D(А) )D(А)  D(E) = 1 и, следовательно, D(А) D(E) = 1 и, следовательно, D(А)  0. 0.
 Достаточность. Пусть D(А) Достаточность. Пусть D(А)  0. Рассмотрим квадратную матрицу n-го порядка 0. Рассмотрим квадратную матрицу n-го порядка  , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы  , транспонированной к матрице А: , транспонированной к матрице А:
.
Легко показать, что
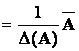  Отсюда следует, что если в качестве обратной матрицы взять матрицу A Отсюда следует, что если в качестве обратной матрицы взять матрицу A  , то произведения A , то произведения A  AиAA AиAA  равны равны
единичной матрицеE n-го порядка: A  A A  AA AA   E. E.
12-ый вопрос
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
| Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
| Для того чтобы линейная система являлась совместной, необходимо и достаточно, что бы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Доказательство (условия совместности системы)
Необходимость
Пусть система совместна. Тогда существуют числа  такие, что такие, что  . Следовательно, столбец . Следовательно, столбец  является линейной комбинацией столбцов является линейной комбинацией столбцов 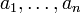 матрицы матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что  . .
]Достаточность
Пусть  . Возьмем в матрице . Возьмем в матрице  какой-нибудь базисный минор. Так как какой-нибудь базисный минор. Так как 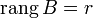 , то он же и будет базисным минором и матрицы , то он же и будет базисным минором и матрицы  . Тогда согласно теореме о базисном миноре последний столбец матрицы . Тогда согласно теореме о базисном миноре последний столбец матрицы  будет линейной комбинацией базисных столбцов, то есть столбцов матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы  . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы  . .
13-ый вопрос
Неоднородной системой линейных уравнений называется система вида:

  — её расширенная матрица. — её расширенная матрица.
Теорема (об общем решении неоднородных систем).
Пусть 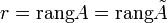 (т.е. система (2) совместна), тогда: (т.е. система (2) совместна), тогда:
· если  , где , где  — число переменных системы (2), то решение (2) существует и оно единственно; — число переменных системы (2), то решение (2) существует и оно единственно;
· если 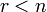 , то общее решение системы (2) имеет вид , то общее решение системы (2) имеет вид 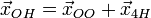 , где , где  — общее решение системы (1), называемое общим однородным решением, — общее решение системы (1), называемое общим однородным решением, 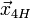 — частное решение системы (2), называемое частным неоднородным решением. — частное решение системы (2), называемое частным неоднородным решением.
14-ый вопрос
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) влинейной алгебре — это система уравнений вида

| (1)
|
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь  — количество уравнений, а — количество уравнений, а  — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2]. — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Векторная форма записи
Система уравнений может быть записана в векторном виде:
A1x1 + A2x2 + ... + Anxn =B

Матричная форма записи
В матричной записи система линейных уравнений может быть записана следующим образом:
AX=B
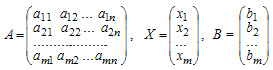
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
| Совместность см выше
15-ый вопрос
Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.
Далее не знаю----------------------------------------------------------------------------------------------------------------------------------------------------
16-ый вопрос
17-ый вопрос
18-ый вопрос
Теорема (о базисном миноре): Пусть 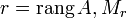 — базисный минор матрицы — базисный минор матрицы  , тогда: , тогда:
базисные строки и базисные столбцы линейно независимы;
любая строка (столбец) матрицы  есть линейная комбинация базисных строк (столбцов).Если есть линейная комбинация базисных строк (столбцов).Если  — квадратная матрица, и — квадратная матрица, и 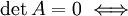 , то строки и столбцы этой матрицы линейно зависимы. , то строки и столбцы этой матрицы линейно зависимы.
Теорема 3.1 о базисном миноре. В произвольной матрице 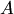 каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Действительно, без ограничения общности предполагаем, что в матрице 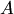 размеров размеров  базисный минор расположен в первых базисный минор расположен в первых  строках и первых строках и первых  столбцах. Рассмотрим определитель столбцах. Рассмотрим определитель
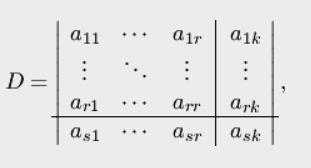
который получен приписыванием к базисному минору матрицы 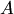 соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых  и и  этот определитель равен нулю. Если этот определитель равен нулю. Если 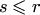 или или  , то определитель , то определитель 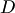 содержит две одинаковых строки или два одинаковых столбца. Если же содержит две одинаковых строки или два одинаковых столбца. Если же  и и  , то определитель , то определитель 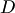 равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем
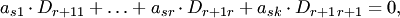
где  — алгебраические дополнения элементов последней строки. Заметим, что — алгебраические дополнения элементов последней строки. Заметим, что  , так как это базисный минор. Поэтому , так как это базисный минор. Поэтому
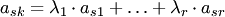 , где , где 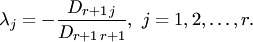
Записывая последнее равенство для  , получаем , получаем
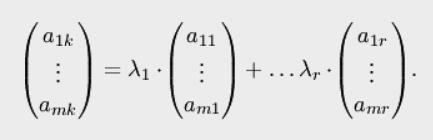
т.е.  -й столбец (при любом -й столбец (при любом  ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать. ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 найден ненулевой минор
найден ненулевой минор 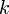 -го порядка
-го порядка  . Рассмотрим все миноры
. Рассмотрим все миноры  -го порядка, включающие в себя (окаймляющие) минор
-го порядка, включающие в себя (окаймляющие) минор 
 , полученная из исходной матрицы
, полученная из исходной матрицы 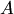 конечным числом элементарных преобразований, называется эквивалентной. Это обозначается
конечным числом элементарных преобразований, называется эквивалентной. Это обозначается  .
.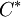 (союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
(союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
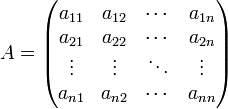 Где:
Где: — алгебраические дополнения исходной матрицы;
— алгебраические дополнения исходной матрицы;  — элементы исходной матрицы.
— элементы исходной матрицы.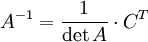
 существует тогда и только тогда, когда исходная матрицаАневырожденная.
существует тогда и только тогда, когда исходная матрицаАневырожденная. AA
AA  0.
0. Достаточность. Пусть D(А)
Достаточность. Пусть D(А)  , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы
, называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы  , транспонированной к матрице А:
, транспонированной к матрице А: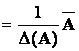
 Отсюда следует, что если в качестве обратной матрицы взять матрицу A
Отсюда следует, что если в качестве обратной матрицы взять матрицу A  такие, что
такие, что  . Следовательно, столбец
. Следовательно, столбец  является линейной комбинацией столбцов
является линейной комбинацией столбцов 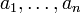 матрицы
матрицы  .
. . Возьмем в матрице
. Возьмем в матрице 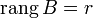 , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы  . Тогда согласно теореме о базисном миноре последний столбец матрицы
. Тогда согласно теореме о базисном миноре последний столбец матрицы 

 — её расширенная матрица.
— её расширенная матрица.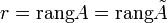 (т.е. система (2) совместна), тогда:
(т.е. система (2) совместна), тогда: , где
, где  — число переменных системы (2), то решение (2) существует и оно единственно;
— число переменных системы (2), то решение (2) существует и оно единственно;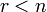 , то общее решение системы (2) имеет вид
, то общее решение системы (2) имеет вид 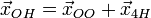 , где
, где  — общее решение системы (1), называемое общим однородным решением,
— общее решение системы (1), называемое общим однородным решением, 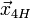 — частное решение системы (2), называемое частным неоднородным решением.
— частное решение системы (2), называемое частным неоднородным решением.
 — количество уравнений, а
— количество уравнений, а  — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
— количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
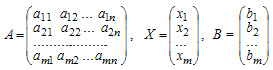
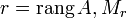 — базисный минор матрицы
— базисный минор матрицы 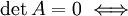 , то строки и столбцы этой матрицы линейно зависимы.
, то строки и столбцы этой матрицы линейно зависимы. базисный минор расположен в первых
базисный минор расположен в первых  строках и первых
строках и первых 
 и
и  этот определитель равен нулю. Если
этот определитель равен нулю. Если 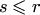 или
или  , то определитель
, то определитель 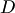 содержит две одинаковых строки или два одинаковых столбца. Если же
содержит две одинаковых строки или два одинаковых столбца. Если же  и
и  , то определитель
, то определитель 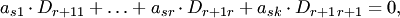
 — алгебраические дополнения элементов последней строки. Заметим, что
— алгебраические дополнения элементов последней строки. Заметим, что  , так как это базисный минор. Поэтому
, так как это базисный минор. Поэтому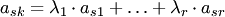 , где
, где 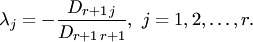
 , получаем
, получаем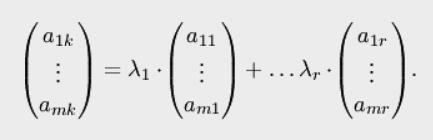
 -й столбец (при любом
-й столбец (при любом