
|
|
С помощью матрицы алгебраических дополнений12 Виды матриц 1. Прямоугольные: m и n - произвольные положительные целые числа 2. Квадратные: m=n
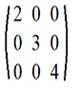
5. Диагональная матрица: m=n и aij=0, если i≠j
7. Нулевая матрица: aij=0, i=1,2,...,m j=1,2,...,n
Например,
Пример. Ясно,A'=-A Матрицы одинакового размера называют одинаковыми ,если попарно равны их соответствующие элементы. Пусть Произведением матрицы Умножение матриц (обозначение:
Количество столбцов в матрице Транспонированная матрица С каждой матрицей
Такая матрица называется транспонированной матрицей для Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица размера Свойства транспонированных матриц
1.
4. существует матрица 5. ;
. Ой вопрос Умножение матриц Умножение матриц (обозначение:
Количество столбцов в матрице Свойства умножения матриц: 1.ассоциативность (AB)C = A(BC); 2.некоммутативность (в общем случае): AB 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC; 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB); 3-ий вопрос Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
Теорема 11.1. Если квадратная матрица А имеет обратную матрицу, то обратная матрица единственная. Предположим, что матрица A имеет две обратные матрицы В и В0. Тогда, согласно определению 11.1 обратной матрицы, выполнены, в частности, равенства AB0= E и BA = E. Используя ассоциативность умножения матриц, получаем B = BE = В (AB0) = (BA)В0= EB0= B0, т.е.матрицы B и B0 совпадают. I Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA ≠ 0 . Метод Гаусса—Жордана Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1. С помощью матрицы алгебраических дополнений
Ый вопрос Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителемсостоит в следующем.;
Умножим это матричное уравнение слева на Так как
КРАМЕРА ПРАВИЛО :если определитель Dквадратной системы линейных уравнений
Здесь 5-ый вопрос Минор Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Теорема (о базисном миноре): Пусть базисные строки и базисные столбцы линейно независимы; любая строка (столбец) матрицы Вторая часть 6-ого вопроса (Следствие 12.1. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы ее строки (столбцы) были линейно независимы.) Н е о б х о д им о с т ь. Если квадратная матрица A невырождена, то ее ранг равен ее порядку, а ее определитель является базисным минором. Поэтому все строки (столбцы) являются базисными и по теореме 12.5 о базисном миноре они линейно независимы. До с т а т о ч н о с т ь. Если все строки (столбцы) квадратной матрицы A являются линейно независимыми, то они являются базисными. Действительно, если бы только некоторые из них были базисными, то, согласно теореме 12.5 о базисном миноре, оставшиеся были бы линейными комбинациями базисных и, следовательно, строки (столбцы) матрицы A, согласно теореме12.4, были бы линейно зависимыми. Так как все строки и столбцы квадратной матрицы A являются базисными, а им соответствует определитель матрицы, то он является базисным минором и, следовательно, согласно определению 12.4, отличен от нуля, т.е. квадратная матрица A невырождена. 7-ой вопрос Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Элементарными преобразованиями строк называют: 1 перестановка местами любых двух строк матрицы; 2 умножение любой строки матрицы на константу 3 прибавление к любой строке матрицы другой строки. Аналогично определяются элементарные преобразования столбцов. 8-ой вопрос Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля Существует несколько методов нахождения ранга матрицы: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором
3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором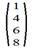 4. Матрица столбец: n=1. Например
4. Матрица столбец: n=1. Например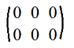
 6. Единичная матрица: m=n и
6. Единичная матрица: m=n и 8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
8. Треугольная матрица: все элементы ниже главной диагонали равны 0. Пример. 9. Симметрическая матрица:m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA'=A
Пример. 9. Симметрическая матрица:m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA'=A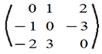 10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=jимеем aii=-aii)
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=jимеем aii=-aii)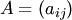 и
и 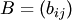 — матрицы одинаковых размеров
— матрицы одинаковых размеров  . Матрица
. Матрица  тех же размеров
тех же размеров 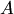 и
и  , если ее элементы равны сумме соответствующих элементов матриц
, если ее элементы равны сумме соответствующих элементов матриц 
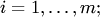
 . Сумма матриц обозначается
. Сумма матриц обозначается 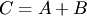 . Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно:
. Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно: называется матрица
называется матрица 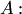
 , реже со знаком умножения
, реже со знаком умножения  ) — есть операция вычисления матрицы
) — есть операция вычисления матрицы 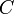 , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.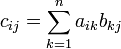
 должно совпадать с количеством строк в матрице
должно совпадать с количеством строк в матрице  , иными словами, матрица
, иными словами, матрица 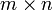 ,
, 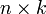 , то размерность их произведения
, то размерность их произведения 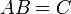 есть
есть 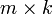 .
.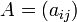 размера
размера  размера
размера 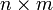 вида
вида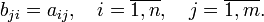
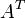 .
. Дважды транспонированная матрица А равна исходной матрице А.
Дважды транспонированная матрица А равна исходной матрице А.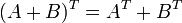 Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированная сумма матриц равна сумме транспонированных матриц.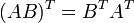 Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке. При транспонировании можно выносить скаляр.
При транспонировании можно выносить скаляр. Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель транспонированной матрицы равен определителю исходной матрицы.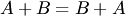 (коммутативность сложения);
(коммутативность сложения);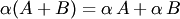 2. (ассоциативность сложения);
2. (ассоциативность сложения); 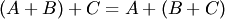
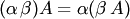 3. существует нулевая матрица
3. существует нулевая матрица 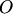 (тех же размеров, что и
(тех же размеров, что и 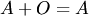 ;
; , противоположная матрице
, противоположная матрице 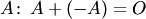 ;
;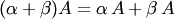
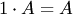
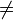 BA;3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;
BA;3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;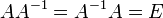
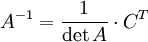
 — транспонированная матрица алгебраических дополнений
— транспонированная матрица алгебраических дополнений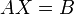 , где
, где  — столбцы свободных членов и решений системы соответственно
— столбцы свободных членов и решений системы соответственно — матрицу, обратную к матрице
— матрицу, обратную к матрице 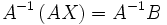
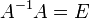 , получаем
, получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: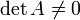 .
.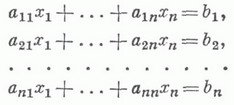 не равен нулю, то эта система имеет единственное решение и это решение находится по формулам
не равен нулю, то эта система имеет единственное решение и это решение находится по формулам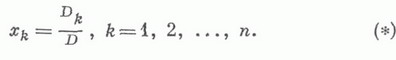
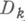 - определитель, получаемый из Dзаменой k-то столба на столбец свободных членов.
- определитель, получаемый из Dзаменой k-то столба на столбец свободных членов. матрицы
матрицы 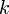 (который называется также порядком этого минора), элементы которой стоят в матрице
(который называется также порядком этого минора), элементы которой стоят в матрице 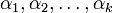 и столбцов с номерами
и столбцов с номерами  .
.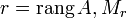 — базисный минор матрицы
— базисный минор матрицы 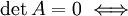 , то строки и столбцы этой матрицы линейно зависимы.
, то строки и столбцы этой матрицы линейно зависимы.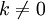 ;
;