
|
|
Линейные уравнения высших порядков12 3.1. Однородное уравнение Определение. Линейным уравнением n-го порядка называется уравнение вида:
Если при всех рассматриваемых значениях xфункция Предполагаем, что коэффициенты
причём начальные данные Заметим, что линейное однородное дифференциальное уравнение (ЛОДУ) всегда имеет нулевое решение Для построения общего решения ЛОДУ достаточно знать n линейно независимых в интервале
(где
был отличен от нуля хотя бы в одной точке из интервала Если найдена фундаментальная система решений
где 3.2. Линейное однородное дифференциальное уравнение Линейное однородное дифференциальное уравнение с постоянными коэффициентами имеет вид:
где
определено в области Построение фундаментальной системы решений ЛОДУ проводится методом Эйлера, который состоит в том, что частное решение ЛОДУ ищется в виде
Его корни называются характеристическими числами уравнения (3.3). Рассмотрим возможные ситуации, возникающие при решении характеристического уравнения. 1. Все корни характеристического уравнения (3.4) различны и вещественны. Обозначим их
2. Все корни характеристического уравнения (3.4) различны, но среди них имеются комплексные. Пусть
Записав линейно независимые частные решения, соответствующие другим сопряжённым парам комплексных корней и всем вещественным корням, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (3.3). 3. Среди корней характеристического уравнения имеются кратные. Пусть 4. Если
В формуле общего решения этим корням соответствует выражение вида:
Записав линейно независимые частные решения указанного выше вида, соответствующие всем простым и кратным вещественным корням, а также сопряжённым парам простых и кратных комплексных корней, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (3.3). 4. Системы обыкновенных 4.1. Нормальные системы Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:
где Определение 2. Пусть дана нормальная система уравнений
где Задача нахождения решения Теорема существования и единственности решения задачи Коши.Пусть дана система уравнений (4.2) и пусть в некоторой области D(x, y, z) функции 4.2. Метод исключения Продифференцируем, например, первое уравнение системы уравнений (4.2) по независимой переменной x:
Вместо системы (4.2) запишем систему уравнений:
Из первого уравнения системы (4.3) следует, что
Итак, исключив из системы функцию z приходим к одному уравнению 2-го порядка, решая которое, получаем: Теперь продифференцируем найденное выражение по x и подставим в функцию В результате заключаем, что решение примет вид:
Определение. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (4.4), непрерывно дифференцируемых на некотором интервале 4.3. Линейные однородные системы Определение. Линейной однородной системой дифференциальных уравнений (ЛОС ДУ) для функций
где Свойства решений ЛОС ДУ (4.5). 1. Сумма двух решений системы (4.5) – тоже решение этой системы. Доказательство: Пусть Тогда
Но Аналогично рассматривается и второе уравнение системы (4.5). 2. Если Доказательство свойства аналогично доказательству свойства 1. Следствие. Если
где Определение 1. Система функций
следует, что В противном случае система функций Определение 2. Определитель, составленный для системы функций
Теорема 1. Определитель Вронского для линейно независимой на интервале Доказательство. Докажем теорему методом от противного. Предположим, что существует точка
Составим линейную однородную систему уравнений с неизвестными
Так как определитель системы (4.7) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть
Согласно следствию из свойств решений ЛОС ДУ функции (4.8) являются решениями системы (4.5), которые в силу равенств (4.7) в точке
Но таким решением может быть только нулевое решение:
Причём Определение 2. Линейно независимые на интервале Теорема 2. Если семейство функций
где Доказательство. 1. Равенства (4.9), согласно следствию из свойств решений ЛОС ДУ, определяют решение системы уравнений (4.5). 2. Докажем, что равенства (4.9) определяют общее решение (4.5), для этого докажем, что каковы бы ни были начальные условия задачи Коши
будет удовлетворять этим условиям. Для этого подставим в равенства (4.9) начальные условия, получим:
Определителем этой алгебраической системы линейных уравнений является определитель Вронского
который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (4.10) имеет решение 4.4. ЛОС ДУ с постоянными коэффициентами Линейная однородная система дифференциальных уравнений с постоянными коэффициентами имеет вид
где Продифференцируем обе функции по x и подставим в уравнения системы (4.11):
Сокращаем оба уравнения системы на
Так как
Уравнение (4.13) называется характеристическим уравнением, а его корни – характеристическими числами системы (4.11). Каждому из корней характеристического уравнения соответствует хотя бы одно частное решение указанного выше вида. Различают три случая. 1. Оба корня характеристического уравнения вещественны и различны:
То же самое проделываем со вторым корнем характеристического уравнения
Следовательно, согласно теореме 2раздела4.3. общим решением системы (4.11) будет следующее семейство функций:
2. Если
Отделив вещественную и мнимую части, получим два вещественных линейно независимых частных решения системы (4.11), соответствующих корню Итак, общее решение ЛОС ДУ в этом случае примет вид:
3.
где Пример. Найти общее решение системы:
Решение: Будем искать решение в виде
Его корни:
Продифференцируем y(x) и подставим
Отсюда после сокращения на
Приравняем в этом тождестве множители при одинаковых степенях x. В результате получим: Итак, общее решение заданной системы уравнений имеет вид:
где 4.5. Линейные неоднородные системы Определение 1. Линейной неоднородной системой дифференциальных уравнений (ЛНС ДУ) называется система уравнений следующего вида
где Теорема 1. Общее решение ЛНС ДУ (4.14) представляет собой сумму общего решения соответствующей ЛОС ДУ (4.5) и какого-либо частного решения системы (4.14):
Доказательство. 1. Прежде всего докажем, что система уравнений (4.15) определяет решение ЛНС ДУ (4.14). Для этого, подставим выражение (4.15) в первое уравнение системы (4.14) и покажем, что в результате получится тождество.
т.е. имеем Аналогичный вывод имеет место и для второго уравнения системы (4.14). 2. Во второй части доказательства докажем, что выражения (4.15) дают общее решение ЛНС. Для этого надо показать, что всегда найдутся числа
Согласно теореме 2раздела4.3. выражения (4.15) можно переписать в виде:
где
или
Определитель этой системы уравнений есть определитель Вронского
но согласно теореме 1 пункта 4.3. Теорема доказана. 4.6. Метод вариации произвольных постоянных Применим метод вариации постоянных, описанный ранее, для решения линейной неоднородной системы дифференциальных уравнений (4.14). Общее решение соответствующей однородной системы (4.5) задаётся парой выражений:
где
где Подставим выражения (4.19) в систему (4.14), получим:
Откуда получаем Аналогично получаем второе уравнение для функций
Итак, для производных
Определитель последней системы есть определитель Вронского для фундаментальной системы решений системы (4.5), который не обращается в нуль ни в одной точке интервала
Интегрируя эти выражения и подставляя результат в систему (4.19), получим ответ. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
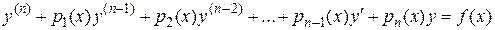 . (3.1)
. (3.1)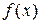 равна нулю, то это уравнение называется однородным, в противном случае – неоднородным.
равна нулю, то это уравнение называется однородным, в противном случае – неоднородным.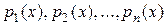 и свободный член
и свободный член  . Тогда уравнение (3.1) имеет единственное решение
. Тогда уравнение (3.1) имеет единственное решение 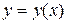 , определённое во всём интервале
, определённое во всём интервале  ,
, можно задавать произвольно, а
можно задавать произвольно, а 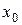 нужно брать из интервала
нужно брать из интервала 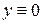 .
.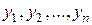 , т.е. таких решений, для которых тождество
, т.е. таких решений, для которых тождество ,
,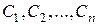 – постоянные числа,) может выполняться только при
– постоянные числа,) может выполняться только при  . Такая система решений называется фундаментальной. Известно, что для того чтобы система решений ЛОДУ была фундаментальной, необходимо и достаточно, чтобы её определитель Вронского
. Такая система решений называется фундаментальной. Известно, что для того чтобы система решений ЛОДУ была фундаментальной, необходимо и достаточно, чтобы её определитель Вронского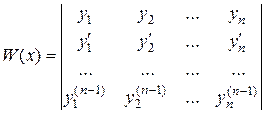
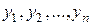 ЛОДУ, то формула
ЛОДУ, то формула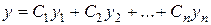 , (3.2)
, (3.2) ,
, 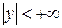 ,
, 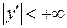 , …,
, …,  .
. , (3.3)
, (3.3) – постоянные вещественные числа. Это уравнение имеет фундаментальную систему решений
– постоянные вещественные числа. Это уравнение имеет фундаментальную систему решений  ,
, 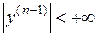 , т.е. во всём пространстве
, т.е. во всём пространстве 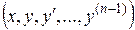 .
.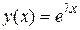 , где
, где 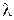 – некоторое число, подлежащее определению. Подставляя эту функцию в уравнение (3.3) и сокращая на
– некоторое число, подлежащее определению. Подставляя эту функцию в уравнение (3.3) и сокращая на  ,получим характеристическое уравнение:
,получим характеристическое уравнение: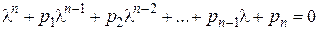 . (3.4)
. (3.4)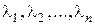 . Тогда фундаментальную систему решений составляют функции:
. Тогда фундаментальную систему решений составляют функции: 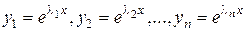 , а общее решение имеет вид:
, а общее решение имеет вид: .
. – комплексный корень характеристического уравнения. Тогда
– комплексный корень характеристического уравнения. Тогда 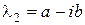 тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых частных решений:
тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых частных решений: ,
, .
. , а в формуле общего решения – выражение вида
, а в формуле общего решения – выражение вида 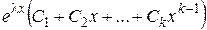 .
.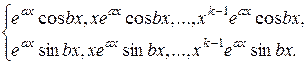
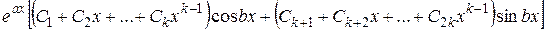 .
.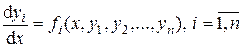 , (4.1)
, (4.1)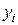 ,
,  – неизвестные функции от независимой переменной x, подлежащие определению;
– неизвестные функции от независимой переменной x, подлежащие определению;  ,
,  , заданные и непрерывные в некоторой области. Число n называется порядком системы (4.1). В дальнейшем ограничимся рассмотрением систем второго порядка (
, заданные и непрерывные в некоторой области. Число n называется порядком системы (4.1). В дальнейшем ограничимся рассмотрением систем второго порядка (  ).
).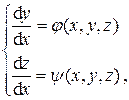 (4.2)
(4.2)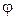 и
и 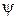 – заданные непрерывные в некоторой области функции. Пара функций
– заданные непрерывные в некоторой области функции. Пара функций  , определённых на интервале
, определённых на интервале 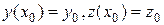 , где
, где  – заданные числа (начальные данные), называется задачей Коши.
– заданные числа (начальные данные), называется задачей Коши.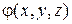 и
и  непрерывны и имеют непрерывные частные производные по y, z. Пусть точка
непрерывны и имеют непрерывные частные производные по y, z. Пусть точка 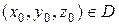 . Тогда существуют интервал
. Тогда существуют интервал 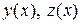 , удовлетворяющие системе уравнений (4.2) и начальным условиям
, удовлетворяющие системе уравнений (4.2) и начальным условиям 
 .
.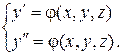 (4.3)
(4.3) . Подставим эту функцию во второе уравнение системы (4.3):
. Подставим эту функцию во второе уравнение системы (4.3): .
.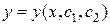 .
. .
.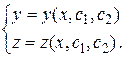 (4.4)
(4.4) (4.5)
(4.5)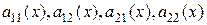 – непрерывные на некотором интервале
– непрерывные на некотором интервале  и
и  – два каких-либо решения системы (4.5).
– два каких-либо решения системы (4.5).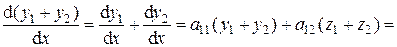
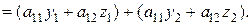
 и
и 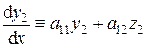 .
. – тоже решение (4.5).
– тоже решение (4.5). и
и  – решения системы (4.5), то выражение вида
– решения системы (4.5), то выражение вида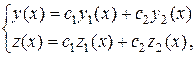
 – произвольные постоянные, тоже решение (4.5).
– произвольные постоянные, тоже решение (4.5).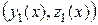 и
и 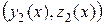 называется линейно независимой на некотором интервале
называется линейно независимой на некотором интервале  (4.6)
(4.6) .
.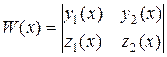 .
.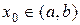 , в которой
, в которой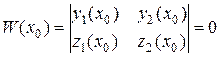 .
.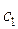 и
и  :
: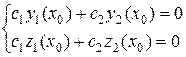 . (4.7)
. (4.7) – одно из них. С помощью этих констант и двух линейно независимых на интервале
– одно из них. С помощью этих констант и двух линейно независимых на интервале  (4.8)
(4.8)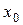 обращаются в нуль. Следовательно,
обращаются в нуль. Следовательно, 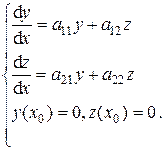
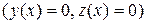 при любом
при любом 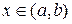 , т.е.
, т.е.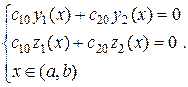
 . Это означает, что система функций
. Это означает, что система функций 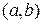 , что противоречит условию теоремы. Значит наше предположение о существовании на интервале
, что противоречит условию теоремы. Значит наше предположение о существовании на интервале  , неверно, что и доказывает теорему.
, неверно, что и доказывает теорему.
 , (4.9)
, (4.9) , всегда найдутся значения постоянных
, всегда найдутся значения постоянных 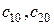 такие, что выделенное из общего частное решение ЛОС ДУ
такие, что выделенное из общего частное решение ЛОС ДУ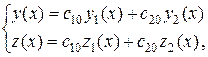
 (4.10)
(4.10) :
: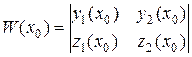 ,
, (4.11)
(4.11) – некоторые постоянные. Система (4.11) имеет фундаментальную систему решений, состоящую из элементарных функций. Основным методом построения фундаментальной системы решений для системы (4.11) является метод Эйлера. Согласно этому методу, решение ЛОС ДУ ищется в виде
– некоторые постоянные. Система (4.11) имеет фундаментальную систему решений, состоящую из элементарных функций. Основным методом построения фундаментальной системы решений для системы (4.11) является метод Эйлера. Согласно этому методу, решение ЛОС ДУ ищется в виде  .
.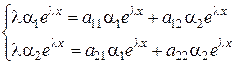 .
. :
: (4.12)
(4.12)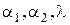 – некоторые постоянные числа, подлежащие определению, среди которых хотя бы одно отлично от нуля, то определитель системы (4.12) должен быть равен нулю
– некоторые постоянные числа, подлежащие определению, среди которых хотя бы одно отлично от нуля, то определитель системы (4.12) должен быть равен нулю . (4.13)
. (4.13) ℝ,
ℝ, 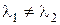 . Подставляем
. Подставляем 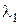 в одно из уравнений системы (4.12), например, в первое уравнение:
в одно из уравнений системы (4.12), например, в первое уравнение:  Из него с точностью до константы определяем
Из него с точностью до константы определяем  , откуда получаем первое решение ЛОС ДУ:
, откуда получаем первое решение ЛОС ДУ: .
. и в результате получаем второе, линейно независимое на
и в результате получаем второе, линейно независимое на  с первым, решение ЛОС ДУ:
с первым, решение ЛОС ДУ: .
. ,
,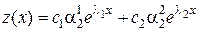 .
. – корень характеристического уравнения, то
– корень характеристического уравнения, то  . Подставляем
. Подставляем  . Теперь составляем первое решение системы (4.11):
. Теперь составляем первое решение системы (4.11):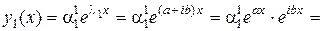
 ,
, .
.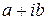 . Решения, соответствующие корню
. Решения, соответствующие корню 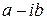 , будут линейно зависимы с решениями, соответствующими корню
, будут линейно зависимы с решениями, соответствующими корню 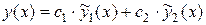
 .
. . В случае кратного корня характеристического уравнения необходимо представить общее решение системы уравнений (4.11) в следующем виде:
. В случае кратного корня характеристического уравнения необходимо представить общее решение системы уравнений (4.11) в следующем виде: ,
,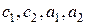 – постоянные числа, причём
– постоянные числа, причём  и
и 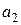 должны быть выражены через
должны быть выражены через 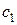 и
и  .
. .
.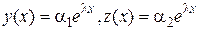 . Характеристическое уравнение:
. Характеристическое уравнение: .
. . Следовательно,
. Следовательно, .
. в первое уравнение исходной системы:
в первое уравнение исходной системы: .
. получаем
получаем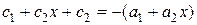 .
.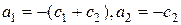 .
.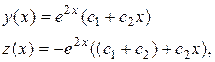
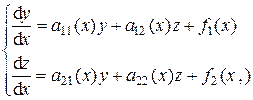 (4.14)
(4.14) – заданные непрерывные на интервале
– заданные непрерывные на интервале 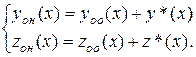 (4.15)
(4.15) ,
, .
.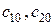 такие, что выделенное из семейства (4.15) частное решение будет удовлетворять начальным условиям
такие, что выделенное из семейства (4.15) частное решение будет удовлетворять начальным условиям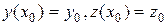 (4.16)
(4.16) (4.17)
(4.17) и
и 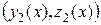 образуют фундаментальную систему решений ЛОС ДУ. Подставим в систему (4.17) начальные условия:
образуют фундаментальную систему решений ЛОС ДУ. Подставим в систему (4.17) начальные условия: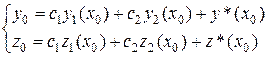
 (4.18)
(4.18) , следовательно, система уравнений (4.18) имеет решение и притом единственное:
, следовательно, система уравнений (4.18) имеет решение и притом единственное:  .
. ,
, (4.19)
(4.19) и
и 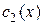 – функции, подлежащие определению.
– функции, подлежащие определению.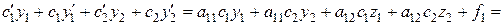
 .
. .
.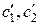 :
: .
. . (4.20)
. (4.20) и
и 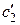 :
: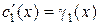 и
и  .
.