
|
|
Аккумулирующая емкость магистрального газопроводаПоследний участок магистрального газопровода от компрессорной станции до города работает с непрерывно изменяющимся отбором газа. Если подачу газа компрессорной станцией в начало газопровода можно считать примерно постоянной, то отбор газа из конца газопровода зависит от режима потребления и при отсутствии газохранилищ строго ему соответствует. Таким образом, работа последнего участка магистрального газопровода характеризуется нестационарным режимом (с непрерывно изменяющейся нагрузкой). В ночное время, когда потребление газа меньше подачи, избыток его накапливается в газопроводе, в результате чего в нем возрастает давление. Количество аккумулированного газа зависит от максимально возможного давления в газопроводе. Если к концу ночного периода в газопроводе будет достигнут максимум давления, т. е. аккумулирующая емкость последнего участка будет исчерпана, а отбор газа из него будет меньше подачи, то придется уменьшить производительность последней компрессорной станции, остановив часть агрегатов. В этом случае накопление газа начнется в предпоследнем участке магистрального газопровода. В дневное время потребление газа превышает подачу, аккумулированный газ поступает из газопровода в город и давление в газопроводе падает. Решение задачи определения аккумулирующей емкости газопровода основано на замене нестационарного режима движения газа стационарным в моменты, когда отбор газа равен потреблению. В действительности, чтобы режим стабилизировался, необходимо некоторое время, так как при непрерывно изменяющемся потреблении стабильная кривая давления устанавливаться не успевает. Приближенное решение предполагает, что в моменты, когда подача газа равна отбору, режим движения в газопроводе стационарен. Аккумулирующая емкость магистрального газопровода, определенная по приближенной методике, оказывается на 10—15%' меньше действительной. Чтобы определить, какое количество газа способен аккумулировать газопровод, следует рассчитать массу газа, находящуюся в сети. Ее находят по следующим уравнениям: dM=Fρdx;
Так как приведенные формулы дают приближенное решение, коэффициент сжимаемости не учитывают.
Расчет аккумулирующей способности последнего участка магистрального газопровода Пример 9.5.1.Определить аккумулирующую емкость последнего участка магистрального газопровода длиной 1=150 км. По газопроводу подается природный газ. Диаметр газопровода 720×10 мм. Максимально допустимое абсолютное давление в газопроводе 55 атм., минимально допустимое абсолютное давление газа перед городом 13 атм. Пропускная способность газопровода, приведенная к нормальным условиям, Q=11000000 м3/сут. Решение Определяем среднее давление в газопроводе в момент максимального накопления газа. Для расчета используем формулу, приведенную в СНиП 2.04.08-87 для турбулентного режима. Вторым слагаемым, данным в скобках, в формуле пренебрегаем
1. Расчет производим для следующих значений: kэ = 0,01 см; d = 70 см; ρ=0,73 кг/м3; l=150000 м;
2. Определяем среднее давление в газопроводе в момент минимального количества газа в нем
3. Определяем геометрический объем газопровода V = 0,785 · 0,72 ·150000 = 57700 м3. 4. Находим аккумулирующую емкость газопровода Qak = 57700(44 – 33,6) = 600000 м3, или
ЧАСТЬ II. СЖИЖЕННЫЙ УГЛЕВОДОРОДНЫЙ ГАЗ (СУГ) Диаграммы состояния СУГ Все основные характеристики пропана и н-бутана: плотность, удельный объем, теплоемкость, энтальпия жидкости, насыщенных и перегретых паров в зависимости от температуры и другие — могут быть легко и с допустимой для практики точностью найдены по диаграммам состояния вещества, которые были предложены Институтом газа АН УССР (рис. 9.17, 9.18). Схема их построения приведена на рис. 9.16. На горизонтальных осях диаграмм отложены значения энтальпии, I, а на вертикальной — значения постоянного давления насыщенных и перегретых паров р. Жирной линией нанесена пограничная кривая ЖКП, состоящая из двух частей: кривой ЖК, характеризующей состояние жидкости, и кривой ПК, характеризующей состояние насыщенного пара. Между этими кривыми проведены из критической точки к линии постоянной сухости пара КХ (X, кг/кг). Удельные объемы (υ, м3/кг) показаны в области жидкости линиями ОБ, а в области пара О'Б'В. Линии постоянной температуры (t, °C) показаны: в докритической зоне (ниже точки К) ломаной кривой ТЕМП, а в сверхкритической зоне (выше точки К) главной кривой Т'Е'. Линии постоянной энтропии [S, кДж/(кг·°С)] показаны кривыми АД. Пользование приведенными диаграммами состояния показано на примерах.
Рис. 9.16. Схема построения диаграмм состояния
Пример 9.6.1.Определить упругость насыщенных паров жидкого пропана, находящегося в резервуаре, если температура жидкости равна +20 °С. Решение Находят пересечение линии постоянной температуры, соответствующей +20 °С (линия ТЕ на рис. 9.16), с пограничной кривой насыщенного пара (линия ПК). Затем через точку пересечения проводится линия; параллельная линии постоянного давления, и на оси ординат отсчитывается упругость паров насыщенного пропана. Для настоящего примера эта упругость равна 0,84 МПа (абс.). Упругость паров пропана при температуре +20 °С равна 0,833 МПа (абс.). Если линия постоянной температуры не пересекает пограничную кривую насыщенного пара (линия Т'Е' на рис. 9.16), то это свидетельствует, что при этой температуре пропан никаким давлением не может быть превращен в жидкость, так как его температура выше критической. Пример 9.6.2.Определить удельный объем и плотность жидкой и паровой фаз пропана в условиях примера 9.6.1. Решение Удельный объем жидкого пропана находится в точке пересечения линии постоянной температуры с пограничной кривой жидкости, а удельный объем насыщенных паров — в точке пересечения этих линий с пограничной кривой пара. Для данного примера удельный объем находится по рис. 9.17: υж = 0,00196 м3/кг, а удельный объем насыщенного пара υп = 0,058 м3/кг. Точные значения этих величин: υж = 0,002004 м3/кг, υп=0,056 м3/кг. Плотности жидкости и пара определяются по известным формулам: ρж=1:0,00186 = 510,2 кг/м3, ρп = 1: 0,058= 18,24 кг/м3. Пример 9.6.3.Определить скрытую теплоту испарения жидкого пропана при условиях примера 9.6.1. Решение Скрытая теплота испарения определяется по разности энтальпий насыщенного пара и жидкости. Энтальпия жидкости находится на оси абсцисс по точке пересечения линии постоянной температуры (или постоянного давления) с пограничной кривой жидкости, а энтальпия насыщенного пара — по точке пересечения этих линий с пограничной кривой насыщенного пара. Для условий примера энтальпия жидкости iж = 140,7 кДж/кг и энтальпия насыщенного пара Iн.п=495,6 кДж/кг. Скрытая теплота испарения λ=iн.п—Iж = 495,6—140,7=354,9 кДж/кг, ее значение 345,67 кДж/кг. Пример 9.6.4.Определить количество тепла, необходимое для испарения 100 кг жидкого пропана и перегрева его паров до 20 °С под давлением 0,5МПа (абс.). Решение Энтальпия кипящей жидкости по рис. 9.17 Iж = 100,8 кДж/кг. Энтальпия перегретого пара (точка пересечения линии постоянного давления и кривой постоянной температуры) Iп.п = 512,4 кДж/кг. Теплота испарения 1 кг жидкости и перегрева 1 кг пара q=Iп.п—Iж = 512,4—100,8=411,6 кДж/кг. Количество тепла, необходимое для испарения 100 кг жидкого пропана и перегрева его паров до 20 °С Q = 411,6·100 = 41160 кДж/кг. Для условий примера по той же диаграмме определяют температуру кипения жидкости tк..ж = +1 °С (приближенно эта же температура соответствует упругости паров). Скрытая теплота испарения λ=478,8—100,8=378 кДж/кг. Теплота перегрева паров qпер = q—λ = 411,6—378 = 33,6 кДж/кг.
Пример 9.6.5.Определить количество пара, которое образуется при дросселировании жидкого пропана от 0,8 до 0,2 МПа (абс.), и температуру в конце дросселирования.
Решение Дросселирование жидкости проходит по линии постоянной энтальпии от точки пересечения линии постоянного давления с пограничной кривой жидкости (точка М на рис. 9.16) до точки пересечения постоянной энтальпии с заданной линией постоянного давления (точка X' на рис. 9.16). Точка пересечения заданной линии постоянного давления с линией постоянной энтальпии и кривой постоянной сухости пара (точка X') показывает, какое количество пара образовалось в результате дросселирования жидкости. Для заданного примера по рис. 9.17 его количество равно 0,25 кг/кг. Температура в конце дросселирования определяется точкой пересечения заданной линии постоянного давления с пограничной кривой пара (точка А на рис. 9.16). Для заданного примера эта температура по рис. 9.17 равна -25 °С. Пример 9.6.6.Определить работу, необходимую для сжатия 1 кг насыщенных паров пропана от 0,2 до 0,8 МПа (абс.), и температуру пара в конце процесса. Процесс сжатия от начального до конечного давления проходит по линии постоянной энтропии. Решение Теоретическая работа сжатия определяется разностью энтальпии в конце процесса (точка Д) и в начале процесса (точка А): ΔIcж—Iд—IA. Температура пара (газа) в конце процесса определяется линией постоянной температуры, проходящей через точку Д. Для заданного примера по рис. 9.17 ΔIcж = 512,4 - 449,4 = 63 кДж/кг. Температура пара в конце процесса сжатия равна +25 °С. Пример 9.6.7.Критическая температура н-бутана Ткр.=425,20К и критическое давление Ркр.=37,5 атм. Определить удельный объем н-бутана при температуре 80 0С и давлении 10 кг/см2. Решение а) Определяем приведенную температуру и приведенное давление
б) По графику рис. 9.3 определяем коэффициент сжимаемости z=0,825 в) удельный объем определяем из уравнения
откуда Задача 9.6.1.Газовая смесь, состоящая из метана - 80%; этана - 8,5%; этилена - 4.8%; пропана - 6% и пропилена - 0,7%, сжата при температуре 600С до 40 ат. Определить плотность газовой смеси (рис. 9.3.) Ответ: ρ = 27,3 кг/м3 Физические свойства СУГ
Пример 9.7.1.Имеется сжиженный газ, весовой состав паровой фазы которого равен: этана – 2,1%; этилена - 1,5%; пропана 64,4%; пропилена – 4,8%; н-бутана - 22%; Бутилена – 5,2%. Необходимо: а) пересчитать весовой состав газа в объемный (молярный); б) определить среднее значение молекулярной массы и плотности, псевдокритическую температуру и давление, газовую постоянную этой смеси и состав жидкой равновесной фазы сжиженного газа. Решение Пересчет весового состава паровой фазы в молярный производится:
Таким образом, состав паровой фазы в объемах (молярных) процентах и объемных долях будет равен: С2Н6=3,18 (0,032); С2Н4=2,44 (0,024); С3Н8=67,35 (0,674); С3Н6=5,25 (0,052); С4Н10=17,5 (0,175); С4Н8=4,28 (0,043);
Средняя молекулярная масса газовой смеси
Средняя плотность газовой смеси при нормальных условиях: а) по закону Авогадро
б) по правилу смешения
где ρ1, ρ2,….ρn - плотность насыщенных паров компонентов сжиженного газа при температуре 0 0С. Псевдокритическая (среднекритическая) температура смеси
Среднекритическое (псевдокритическое) давление
Удельная газовая постоянная газовой смеси заданного выше состава может быть определена по правилу смещения
где R1, R2, .… Rn - удельные газовые постоянные компонентов, входящих в газовую смесь. Rсм=0,021∙28,12+0,015∙30,25+0,644∙19,24+0,048∙20,16+ +0,22∙14,59+0,052∙15,11=18,68 кГм/кг∙град, или 183,1 Дж/кг∙К. Состав жидкой фазы сжиженного газа определяется в следующей последовательности. а) Определяем общее давление равновесной системы пар-жидкость. Согласно объединенному уравнению законов Рауля и Дальтона yiP=xiθi, концентрация компонента в жидкой фазе будет
Так как состав жидкой фазы равен х1+х2+…+хn=1, то из предыдущих двух уравнений можно записать
откуда общее давление системы пар-жидкость равно
или 0,252 МПа, где θ1, θ2, ………θn - упругость компонентов газовой смеси в чистом виде берутся из справочных таблиц. б) По уравнению
Таким образом, состав жидкой фазы в процентах и долях единицы равен: С2Н6 = 0,23 (0,0023); С2Н4 = 0,10 (0,001); С3Н8 = 35,47 (0,3547); С3Н6 = 2,14 (0,0214); С4Н10 = 51,48 (0,5148); С4Н8 = 10,58 (0,1058);
Пример 9.7.2.Критическая температура н-бутана Ткр.=425,20К и критическое давление Ркр.=37,5 атм. Определить удельный объем н-бутана при температуре 80 0С и давлении 10 кг/см2. Решение а) Определяем приведенную температуру и приведенное давление
б) По графику рис. 9.3 определяем коэффициент сжимаемости z=0,825. в) удельный объем определяем из уравнения
откуда Задача 9.7.1.Газовая смесь находится под давлением 3 МПа. Объемная концентрация компонентов смеси: r1=0,4; r2=0,2; r3=0,3; r4=0,1. Определить парциальное давление этих компонентов в смеси. Ответ Р=3 МПа. Задача 9.7.2.Газовая смесь, состоящая из метана - 80%; этана - 8,5%; этилена - 4.8%; пропана - 6% и пропилена - 0,7%, сжата при температуре 600С до 40 ат. Определить плотность газовой смеси. Ответ: ρ = 27,3 кг/м3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

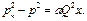
 .
. ;
; ;
; ;
; ;
; =4,4 МПа.
=4,4 МПа. =1,3 МПа;
=1,3 МПа; =4,76 МПа;
=4,76 МПа; =3,36 МПа.
=3,36 МПа. суточной пропускной способности.
суточной пропускной способности.
 Рис. 8.17. Диаграммы состояния пропана
Рис. 8.17. Диаграммы состояния пропана Рис. 8.17. Диаграммы состояния бутана
Рис. 8.17. Диаграммы состояния бутана

 ,
, .
.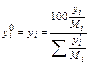 в процентах,
в процентах, в долях единицы.
в долях единицы. ;
; ;
; ;
; или 0,0244;
или 0,0244; или 0,6735;
или 0,6735; или 0,0525;
или 0,0525; или 0,175;
или 0,175; или 0,0428.
или 0,0428. (1).
(1). .
. .
. ,
,

 .
.
 ,
, .
. ,
, ,
, кг/см2
кг/см2 определяем состав жидкой фазы в долях единицы и процентах:
определяем состав жидкой фазы в долях единицы и процентах: (0,23);
(0,23); (0,1);
(0,1); (35,47);
(35,47); (2,14);
(2,14); (51,48);
(51,48); (10,58).
(10,58).
 .
. ,
, .
. .
.