
|
|
Критические параметры газовЧАСТЬ I. ПРИРОДНЫЙ ГАЗ Простейшие расчеты природного и идеального газов Расчёт параметров природного газа при нормальных условиях Примеры расчёта основных параметров природного газа
В качестве примеров рассчитаем основные параметры природного газа - плотность при нормальных условиях, критические температуры и давления, коэффициент сжимаемости, а также влажность газа. Пример 9.1.1. Расчёт критических и приведённых температур и давлений. Определим при нормальных условиях при следующих данных по составу и объёмному содержанию его компонентов, %: метан-93, этан-4, пропан-1, бутан-0,6, пентан-0,2, углекислый газ-0,2, азот-1. По справочным данным определим плотность входящих в смесь газовых компонентов при нормальных условиях, кг/м3: метан-0,668, этан-1,263, пропан-1,872, бутан-2,519, пентан-3,221, углекислый газ-1,842, азот-1,166. Рассчитаем плотность газовой смеси ρн.см=(1/100) (93∙0,668 + 4∙1,263 + 1∙1,872 + 0,6∙2,519 + 0,2∙3,221 + 0,2∙1,842 + +1∙1,166)=0,727кг/м3 Расчёт критических и приведённых температур и давлений. Определим приведенные температуру и давление смеси природного газа следующего состава: метан-92%, этан-4%, пропан-2%, пентан-1% при температуре Т =293 К и избыточном давлении ризб=2,942 МПа. Барометрическое давление рб=0,101357 МПа. Из табл. 9.1.1 возьмём критические температуры и давления компонентов природного газа: для метана Ткр1=191 К, ркр1=4,639 МПа; для этана Ткр2=305 К, ркр2=4,88 МПа; для пропана Ткр3=370 К, ркр3=4,256 МПа; для бутана Ткр4=425,4 К, ркр4=3,795 МПа; для пентана Ткр5=470 К, ркр5=3,373 МПа. По критическим давлениям и температурам отдельных газовых компонентов вычислим критические температуру и давление смеси Ткр.см=(1/100) (92∙191 + 4∙305 + 2∙370 + 1∙425,2 + 1∙470)=203,5 К; ркр.см=(1/100) (92∙4,639 + 4∙4,88 + 2∙4,256 +1∙3,795 + 1∙3,373)=4,62 МПа. Таблица 9.1.1 Критические параметры газов
Приведённые температуру и давление выбранной смеси газов для заданного избыточного давления смеси ризб=2,942 МПа и температуры газа Т=293 К определим Тпр.см=Т/ Ткр.см=293/203,5=1,44 рпр.см=р/ ркр.см=3,043/4,62=0,66 где р=ризб + рб=2,942+0,101=3,043 МПа – абсолютное давление газа. Пример 9.1.2. Рассчитаем критические давление и температуру газовой смеси с плотностью при нормальных условиях ρн.см=0,7763 кг/м3 для газовой смеси, не содержащей азот и углекислый газ, а также содержащей азот с объёмной концентрацией 1% и углекислый газ с концентрацией 0,5%. Для газа, не содержащего азот и углекислый газ, определим критические параметры ркр= 4,757 - 0,1773 ρн.см=4,757 - 0,1773∙0,7763=4,619 МПа; Ткр=87,5 + 155,24 ρн.см=87,5 + 155,24∙0,7763=208 К. Для расчёта критических параметров газовой смеси с объёмным содержанием азота 1% и углекислого газа 0,5% предварительно определим концентрацию азота и углекислого газа в долях единицы, т.е. N2=1:100=0,01 и CO2=0,5:100=0,005. Определим критические параметры смеси газов с содержанием азота и углекислого газа ркр=4,757 - 0,1773 ρн.см – 1,160 N2 + 2,958 CO2=4,757 – 0,1773∙0,7763 –1,160∙0,01 + +2,958∙0,005= 4,622 МПа; Ткр=87,5 + 155,24 ρн.см – 148,35 N2 – 88,25 CO2 = 87,5 +155,24∙0,7763 – 148,35∙0,01 – -88,25∙0,005 = 206,1 К. Пример 9.1.3. Расчёт коэффициента сжимаемости природного газа в рабочих условиях. Рассчитаем коэффициент сжимаемости природного газа при следующих значениях параметров газа: плотность газа при нормальных условиях рн.=0,76 кг/м3, избыточное давление газа ризб=0,78 МПа, температура газа t = -9,5 оС, барометрическое давление рб=0,1 МПа, концентрация азота 1%, углекислого газа – 0,5%. Для расчета коэффициента сжимаемости предварительно определим абсолютное давление газа р, а также критические и приведённые температуры и давления. Абсолютное давление газа р определяется выражением р= ризб + рб = 0,78 + 0,1=0,88 МПа, а абсолютная температура газа Т= t + 273,15 = -9,5 +273,15 = 263,65 К. Определим критические давление и температуру ркр= 4,757 - 0,1773 ρн.см – 1,160 N2 + 2,958 CO2= 4,757 – 0,1773∙0,77 – 1,160∙0,01 + +2,958∙0,005 = 4,62 МПа Ткр=87,5 + 155,24 ρн.см – 148,35 N2 – 88,25 CO2 = 87,5 +155,24∙0,76 – 148,35∙0,01 – 88,25∙0,005 = 203,56 К Определим приведённые давление и температуру рпр = р/ ркр= 0,88/4,62 = 0,191 Тпр= Т/ Ткр= 263,65/203,56 = 1,295 Для расчёта Z найдём значение коэффициентов рс и Тс рс = 0,6714 рпр = 0,6714∙0,191 = 0,128 Тс = 0,71892 Тпр = 0,71892∙1,295 = 0,931 Так значение рс < 1,3, а Тс < 1,09, значение F
Найдем значение
Найдем значение
Далее найдём
Определим
Найдем значение В1
Зная коэффициенты
Определим значение коэффициента сжимаемости Z по приближенной формуле при абсолютном давлении р =0,88 МПа и температуре газа Т=263,6К
Сравнивая значения Z, видим, что они различаются друг от друга не более чем на 0,5%, а это вполне допустимо при выполнении большинства практических расчётов. В качестве примера рассмотрим также определение коэффициента сжимаемости Z в зависимости от приведённых температуры и давления по графикам, показанным на рис. 9.1. На оси абсцисс откладывается значение приведённого давления рпр и восстанавливается перпендикуляр до пересечения с кривой, соответствующей заданной приведённой температуре Тпр. Из точки пересечения перпендикуляра с кривой приведённой температуры проводится горизонтальная прямая до пересечения с осью ординат, на которой отсчитывается искомое значение коэффициента сжимаемости Z. Если заданное значение приведённой температуры находится между двумя кривыми приведённых температур, то производится графическая аппроксимация этих значений. В качестве примера найдём коэффициент сжимаемости Z при рпр=3,41 и Тпр=1,71. отложим на оси абсцисс значение приведённого давления рпр=3,41 (рис. 9.1) и восстановим перпендикуляр до пересечения с кривой приведённой температуры Тпр=1,71. Так как на рис. 9.1 имеются только кривые для Тпр=1,7 и 1,8, то значение Тпр=1,71 находится методом аппроксимации. Из точки пересечения перпендикуляра с кривой для Тпр=1,71 проведём горизонтальную прямую до пересечения с осью ординат, на которой и отсчитываем искомое значение Z=0,86.
Значение Z, определённое по рис. 9.1, по исходным данным предыдущего примера (рпр=0,191 и Тпр=1,295), равно 0,98. Расчёт влажности газа. В качестве примера определим по рис. 9.2 абсолютную влажность газа при его температуре точки росы 5 оС и абсолютном давлении 0,5 МПа. Для этого из точки на оси абсцисс со значением температуры точки росы 5 оС восстановим перпендикуляр до пересечения с кривой, соответствующей давлению 0,5 МПа, и из точки пересечения проведём горизонтальную прямую до пересечения с осью ординат. При этом искомое значение абсолютной влажности газа будет 1,4 г/м3. По рис. 9.2 можно также определить массу воды, выделяющуюся из 1 м3 насыщенного влагой газа при снижении температуры от t1 до t2. Так при снижении температуры стенок трубопровода от t1=10 оС до t2 = -10 оС абсолютная влажность, определённая по рис. 9.2 изменяется от 10 до 2 г/м3, т.е. из каждого 1 м3 газа выделяется 8 г воды.
Рис. 8.2. Зависимость абсолютной влажности природного газа от температуры его точки росы и абсолютного давления Законы идеальных газов Примеры решения задач Пример 9.1.4.Газ при давлении 5 ат (Р1) занимает объем, равный 60 м3 (V1). Какой объем займет газ при 15 ат (Р2) и той же температуре? Решение Согласно закону Бойля-Мариотта при Т=const P2V2=P1V1 Следовательно:
Пример 9.1.5.Коксовый газ, образовавшийся в камере коксовой печи, охладился с 1000 до 500С. Во сколько раз уменьшился объем коксового газа, если давление его не изменилось? Решение Исходя из закона Гей-Люссака при P=const можно записать
Откуда, принимая конечный объем за 1, получим
Пример 9.1.6.Имеется смесь газов под давлением 30 ат (2,94 МПа). Молярная концентрация первого газа r1=0,4; второго r2=0,2; третьего r3=0,3 и четвертого r4=0,1. Определить парциальное давление этих компонентов в смеси. Решение Согласно закону Дальтона Pi=riP, тогда Р1=0,4∙30=12 ат (1,18) МПа Р2=0,2∙30=6 ат (0,59) МПа Р3=0,3∙30=9 ат (0,88) МПа Р4=0,1∙30=3 ат (0,29) МПа Итого Р=30 ат (2,94) МПа Пример 9.1.7.Сжиженный газ состоит из пропана 40%, изо-бутана 25% и н-бутана 35%. Определить парциальное давление компонентов при 400С и состав паровой фазы. Решение Согласно закону Рауля Рi=xiθi (упругость паров θi чистых компонентов при 40 0С равна θ1=1,36 МПа, θ2=0,51 МПа и θ3=0,37 МПа. Парциальное давление компонентов будет равно (в МПа): Р1=0,4∙1,36=0,544 Р2=0,25∙0,51=0,126 Р3=0,35∙0,37=0,129 Р=Р1+Р2+Р3=0,544+0,126+0,129=0,799 Согласно уравнению
Пример 9.1.8.Рассчитать состав растворенного в воде при температуре 0 0С газа, состоящего из 90% метана и 10% этана. Решение При общем давлении в 0,1 МПа (растворение идет при нормальном давлении) парциальное давление метана будет 0,09, а этана 0,01 МПа. Известно, что при температуре 0 0С в 100 см3 воды растворяется 5,56 см3 метана и 9,87 см3 этана. При указанных выше парциальных давлениях будет растворяться: метана 0,9∙5,56=4,91 см3 этана 0,1∙9,89=0,99 см3 Итого 5,9 см3 Состав растворенной газовой смеси (в %): метана 4,91∙100/5,9=83,3 этана 0,99∙100/5,9=16,7.
Задачи для самостоятельного решения
Задача 9.1.1. В цилиндре с подвижным поршнем находится 1 часть кислорода и 1 часть метана в состоянии термодинамического равновесия. Определить соотношение объемов. Ответ: 0,5 Задача 9.1.2.Компрессор подает кислород в резервуар емкостью 3 м3. Избыточное давление его увеличивается от 0,1 до 6 ат, а температура от -15 оС до +30 оС. Определить количество закачанного кислорода, если барометрическое давление 745 мм рт. ст. Ответ: 21,7 кг Задача 9.1.3.Сжатый воздух в баллоне имеет температуру t = 15 oС, давление 4,8 МПа. Во время пожара температура воздуха поднялась до 450оС. 1. Взорвется ли баллон, если известно, что при этой температуре он может выдержать давление не более 9,8 МПа. 2. При t = 800 oС и давлении 1 ат плотность газа 0,45 кг/м3. Определить что это за газ. Ответ: аргон Задача 9.1.4.Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при t = 15 oС. После израсходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10oС. Определить массу израсходованного кислорода. Ответ: 0,606 кг. Задача 9.1.5.В баллоне с метаном первоначальное давление составляло 320 кПа. При той же температуре повысили давление в баллоне
до 5000 кПа. Во сколько раз изменится плотность метана? Ответ: в 15,6 раза. Задача 9.1.6.В газгольдер при температуре 270С закачано 100000 м3 коксового газа. Какой объем будет занимать указанное количество газа при температуре 270 0С. Ответ: 181000 м3. Задача 9.1.7. Под давлением 100 кПа и при температуре 1230С находится 4,2 кг метана. Какой объем занимает метан? Ответ: 0,86 м3. Задача 9.1.8.Какова масса 10 м3 водорода, 10 м3 азота и 10 м3 метана при 10 ат и 1000С? Ответ: H2=6,37 кг; N2 = 88,5 кг; CH4 = 50,6 кг. Задача 9.1.9. Имеются газы: метан - 0,8 м3 при 10 ат (0,98 МПа), этан - 0,6 м3 при ат (0,59 МПа) и пропан - 0,4 м3 при 4 ат (0,39 МПа) Найти давление их смеси в объеме 1 м3 и молярные концентрации. Задача 9.1.10.Определить, сколько углекислоты (СО2) может раствориться в 15 т воды при нормальном давлении и температуре 20 0С.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|




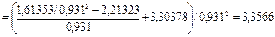








 определим коэффициент сжимаемости природного газа Z в рабочих условиях:
определим коэффициент сжимаемости природного газа Z в рабочих условиях:


 Рис. 9.1. График зависимости коэффициента сжимаемости газов от приведенного давления (рпр) и приведенной температуры (Тпр)
Рис. 9.1. График зависимости коэффициента сжимаемости газов от приведенного давления (рпр) и приведенной температуры (Тпр)
 м3
м3
 раза.
раза. находим состав паровой фазы:
находим состав паровой фазы: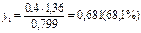

 .
.