
|
|
Механические характеристики асинхронных двигателей
Асинхронные двигатели являются основными двигателями, которые наиболее широко используются как в промышленности, так и в агропромышленном производстве. Они обладают существенными преимуществами перед другими типами двигателей: просты в эксплуатации, надежны и имеют низкую стоимость. В трехфазном асинхронном двигателе при подключении обмотки статора к сети трехфазного переменного напряжения создается вращающееся магнитное поле, которое, пересекая проводники обмотки ротора, наводит в них ЭДС, под воздействием которой в роторе появляются ток и магнитный поток. Взаимодействие магнитных потоков статора и ротора создает вращающий момент двигателя. Появление в обмотке ротора ЭДС, следовательно, и вращающего момента возможно только при наличии разности между скоростями вращения магнитного поля статора и ротора. Это различие в скоростях называют скольжением. Скольжение асинхронного двигателя - это мера того, насколько ротор отстает в своем вращении от вращения магнитного поля статора. Оно обозначается буквой S и определяется по формуле
где w0 - угловая скорость вращения магнитного поля статора (синхронная угловая скорость двигателя); w - угловая скорость ротора; ν – частота вращения двигателя в относительных единицах. Скорость вращения магнитного поля статора зависит от частоты тока питающей сети f и числа пар полюсов р двигателя: Уравнение механической характеристики асинхронного двигателя можно вывести на основе упрощенной схемы замещения, приведенной на рис.2.11. В схеме замещения приняты следующие обозначения: Uф - первичное фазное напряжение; I1 - фазный ток в обмотках статора; I2́ - приведенный ток в обмотках ротора; X1 – реактивное сопротивление обмотки статора; R1, R12 – активные сопротивления в обмотках соответственно статора и приведенного ротора; X2΄- приведенное реактивное сопротивление в обмотках ротора; R0, X0 - активное и реактивное сопротивления контура намагничивания; S – скольжение. В соответствии со схемой замещения на рис.2.11 выражение для тока ротора имеет вид
Рис. 2.11. Схема замещения асинхронного двигателя
Вращающий момент асинхронного двигателя может быть определен из выражения Мw0 S=3(I2΄)2R2΄ по формуле
Подставив значение тока I2΄ из формулы (2.19) в формулу (2.20), определяем вращающий момент двигателя в зависимости от скольжения, т.е. аналитическое выражение механической характеристики асинхронного двигателя имеет вид
График зависимости M=f(S) для двигательного режима представлен на рис.2.12. В процессе разгона момент двигателя изменяется от пускового Mn до максимального момента, который называется критическим моментом Mк. Скольжение и скорость двигателя, соответствующие наибольшему (максимальному) моменту, называют критическими и обозначают соответственно Sк , wк. Приравняв производную
где Хк=(Х1+Х2΄) – реактивное сопротивление двигателя.
Для двигательного режима Sк берется со знаком “плюс”, для сверхсинхронного - со знаком “минус”. Подставив значение Sк (2.22) в выражение (2.21), получим формулы максимального момента: а) для двигательного режима
б) для сверхсинхронного торможения
 (2.24) (2.24)
Знак “плюс” в равенствах (2.22) и (2.23) относится к двигательному режиму и к торможению противовключением; знак “минус” в формулах (2.21), (2.22) и (2.24) - к сверхсинхронному режиму двигателя, работающего параллельно с сетью (при w>w0). Как видно из (2.23) и (2.24), максимальный момент двигателя, работающего в режиме сверхсинхронного торможения, будет больше по сравнению с двигательным режимом из-за падения напряжения на R1 (рис. 2.11). Если выражение (2.21) разделить на (2.23) и произвести ряд преобразований с учетом уравнения (2.22), можно получить более простое выражение для зависимости M=f(S):
где Пренебрегая активным сопротивлением обмотки статора R1, т.к. у асинхронных двигателей мощностью более 10 кВт сопротивление R1 значительно меньше Хк, можно приравнять а ≈ 0, получаем более удобную и простую для расчетов формулу определения момента двигателя по его скольжению (формула Клосса):
В (2.27) любой результат решения под корнем брать со знаком “+”, ибо при знаке “-” решение данного уравнения не имеет смысла. Уравнения (2.21), (2.23), (2.24), (2.25) и (2.26) являются выражениями, описывающими механическую характеристику асинхронного двигателя (рис. 2.12). Искусственные механические характеристики асинхронного двигателя можно получить за счет изменения напряжения или частоты тока в питающей сети либо введения добавочных сопротивлений в цепь статора или ротора. Рассмотрим влияние каждого из названных параметров (U, f, Rд) на механические характеристики асинхронного двигателя. Влияние напряжения питающей сети.Анализ уравнений (2.21) и (2.23) показывает, что изменение напряжения сети влияет на момент двигателя и не влияет на его критическое скольжение. При этом момент, развиваемый двигателем, изменяется пропорционально квадрату напряжения: М≡ kU2, (2.28) где k – коэффициент, зависящий от параметров двигателя и скольжения. Механические характеристики асинхронного двигателя при изменении напряжения сети представлены на рис 2.13. В данном случае Uн= U1>U2>U3. Влияние добавочного внешнего активного сопротивления, включенного в цепь статора. Добавочные сопротивления вводят в цепь статора для уменьшения пусковых значений тока и момента (рис.2.14а). Падение напряжения на внешнем сопротивлении является в данном случае функцией тока двигателя. При пуске двигателя, когда величина тока большая, напряжение на обмотках статора снижается.
Рис.2.14. Схема включения (а) и механические характеристики (б) асинхронного двигателя при включении активного сопротивления в цепь статора
При этом согласно уравнениям (2.21), (2.22) и (2.23) изменяются пусковой момент Мп, критический момент Мк и угловая скорость ωк. Механические характеристики при различных добавочных сопротивлениях в цепи статора представлены на рис.2.14б, где Rд2>R д1. Влияние добавочного внешнего сопротивления, включенного в цепь ротора. При включении добавочного сопротивления в цепь ротора двигателя с фазным ротором (рис.2.15а) его критическое скольжение повышается, что объясняется выражением
а б
Рис.2.15. Схема включения (а) и механические характеристики (б) асинхронного двигателя с фазным ротором при включении добавочного сопротивления в цепь ротора
В выражение (2.23) величина R/2 не входит, так как эта величина не влияет на МК, поэтому критический момент остается неизменным при любом R/2. Механические характеристики асинхронного двигателя с фазным ротором при различных добавочных сопротивлениях в цепи ротора представлены на рис.2.15б. Влияние частоты тока питающей сети. Изменение частоты тока влияет на величину индуктивного сопротивления Xк Механические характеристики двигателя при изменении частоты тока f представлены на рис.2.16.
 Рис.2.16. Механические характеристики асинхронного двигателя при изменении частоты тока питающей сети 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (2.17)
, (2.17) . (2.18)
. (2.18) . (2.19)
. (2.19)
 . (2.20)
. (2.20) . (2.21)
. (2.21) нулю в выражении (2.21), получим значение критического скольжения Sk, при котором двигатель развивает максимальный момент:
нулю в выражении (2.21), получим значение критического скольжения Sk, при котором двигатель развивает максимальный момент: , (2.22)
, (2.22)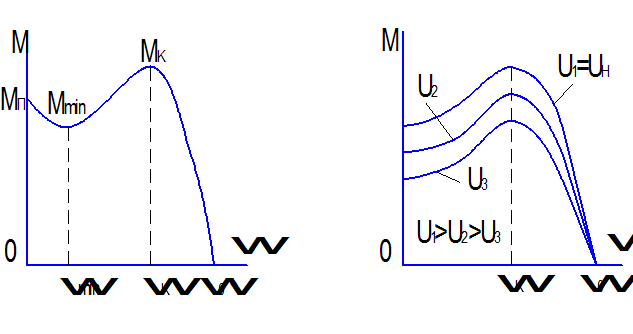
 ; (2.23)
; (2.23) , (2.25)
, (2.25) – коэффициент.
– коэффициент. . (2.26) Если в выражение (2.25) вместо текущих значений M и S подставить номинальные значения и обозначить кратность моментов Mк/Mн через kmax, получим упрощенную формулу для определения критического скольжения:
. (2.26) Если в выражение (2.25) вместо текущих значений M и S подставить номинальные значения и обозначить кратность моментов Mк/Mн через kmax, получим упрощенную формулу для определения критического скольжения: . (2.27)
. (2.27)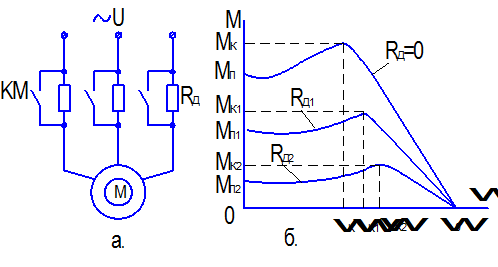
 .
.
 асинхронного двигателя и, как видно из уравнений (2.18), (2.22), (2.23) и (2.24), оказывает влияние на синхронную угловую скорость w0, критическое скольжение Sк и критический момент Mк. Причем
асинхронного двигателя и, как видно из уравнений (2.18), (2.22), (2.23) и (2.24), оказывает влияние на синхронную угловую скорость w0, критическое скольжение Sк и критический момент Mк. Причем  ;
;  ; w0ºf, где C1, C2 - коэффициенты, определяемые параметрами двигателя, не зависящими от частоты тока f.
; w0ºf, где C1, C2 - коэффициенты, определяемые параметрами двигателя, не зависящими от частоты тока f.