|
|
Механические и электромеханические характеристики двигателей постоянного тока независимого возбужденияГлава 2. Характеристики и режимы работы электродвигателей
Схемы включения двигателя постоянного тока независимого и параллельного возбуждения представлены на рис.2.1. При независимом возбуждении (рис.2.1а) обмотка якоря двигателя М и обмотка возбуждения ОВ питаются от разных, независимых друг от друга источников напряжения U и U в, а при параллельном возбуждении (рис.2.1б) - от одного и того же источника U. На практике чаще всего используется схема с параллельным возбуждением. Аналитическое выражение механической характеристики двигателя можно получить из уравнения равновесия напряжений, составленного для якорной цепи по схеме рис.2.1а. При установившимся режиме работы двигателя (магнитный поток возбуждения и угловая скорость якоря постоянны) приложенное напряжение U уравновешивается падением напряжения в якорной цепи IЯR и электродвижущей силой(ЭДС) Е, наведенной в якоре в процессе его вращения, т.е.
где IЯ – ток в якорной цепи двигателя; R=RД+Rя - общее сопротивление якорной цепи, включающее в общем случае внутреннее сопротивление всей якорной цепи двигателя Rя и внешнее добавочное сопротивление RД.
Значение ЭДС определяется по выражению E=kФw, (2.2) где k – коэффициент, зависящий от конструктивных параметров двигателя, Если в (2.1) подставить (2.2) и решить полученное уравнение относительно Iя=I, то получим
Уравнение (2.3) представляет собой зависимость тока якоря от скорости двигателя I=f(w), которая называется электромеханической характеристикой двигателя. Электромеханическая характеристика (по устаревшей терминологии скоростная характеристика) отражает связь между электрической и механической величинами электродвигателя. Для получения уравнения механической характеристики воспользуемся известной зависимостью момента двигателя от магнитного потока и тока якоря: М= kФI. (2.4) Подставив в (2.4) значение тока I, определяемое по выражению (2.3), получим уравнение механической характеристики:
или
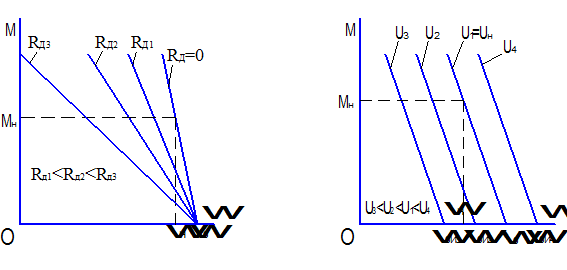
где С=kФ – коэффициент. При неизменных параметрах U, Ф и R выражение (2.5) можно записать в виде М=А-Вw, (2.7) где Анализ уравнений (2.5, 2.6, 2.7) показывает, что механическая характеристика двигателя с независимым возбуждением имеет линейную зависимость и представляет собой прямую линию (рис.2.2). Все электромеханические и механические характеристики электродвигателей разделяют на естественные и искусственные. Характеристики, полученные при номинальных параметрах электродвигателя и отсутствии в его цепях добавочных сопротивлений, называются естественными. Характеристики, полученные при несоблюдении хотя бы одного из этих условий, называются искусственными. Искусственные механические характеристики двигателя постоянного тока, как видно из уравнения (2.5), можно получить за счет изменения напряжения питающей сети U или магнитного потока возбуждения Ф, или сопротивления якорной цепи R путем включения изменения RД в цепь якоря двигателя. Рассмотрим влияние U, Ф, RД на механические характеристики двигателя более подробно. Введение добавочного сопротивления в цепь якоря двигателя. На рис.2.3 представлены механические характеристики двигателя постоянного тока независимого возбуждения при изменении добавочного сопротивления в цепи якоря. Анализ уравнения (2.5), показывает, что при М=0 все характеристики проходят через одну точку, лежащую на оси абсцисс. Угловая скорость в этой точке имеет вполне определенное значение, не зависящее от сопротивления якорной цепи; она называется скоростью идеального холостого ходаwо; определяется по выражению (2.8) путем преобразования уравнения (2.5) при М=0:
Наклон механической характеристики, или ее жесткость, согласно (2.7) зависит от величины добавочного сопротивления в цепи якоря и других параметров. На рис.2.3 показано влияние введенных добавочных сопротивлений в цепь якоря двигателя на его механические характеристики. Введение добавочного сопротивления в якорную цепь используется на практике для регулирования скорости вращения двигателя и ограничения пусковых токов и моментов при его пуске. Изменение напряжения питающей сети. Анализ уравнений (2.5) и (2.8) показывает, что при изменении напряжения, приложенного к якорной цепи двигателя, пропорционально меняется скорость идеального холостого хода. Наклон характеристик остается постоянным. Следовательно, механические характеристики, соответствующие различным значениям напряжения сети, будут между собой параллельны (рис.2.4.), т.е. при изменении U изменяются пусковой ток и момент, скорость идеального холостого хода двигателя. Угол наклона характеристик (жесткость) не меняется.
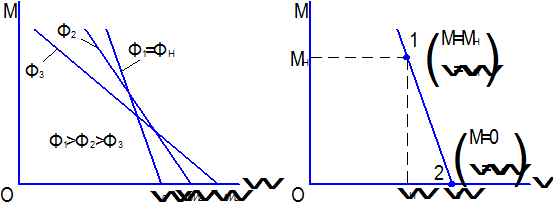
Изменение магнитного потока возбуждения. Анализ уравнений (2.5) и (2.8) показывает, что изменение магнитного потока двигателя оказывает влияние как на первое, так и на второе слагаемое, т.е. изменяются скорость идеального холостого хода и жесткость характеристики. Чем меньше магнитный поток, тем выше скорость идеального холостого хода и тем меньше жесткость механической характеристики. Искусственные механические характеристики двигателя, соответствующие различным величинам магнитного потока возбуждения, представлены на рис.2.5.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
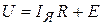 , (2.1)
, (2.1)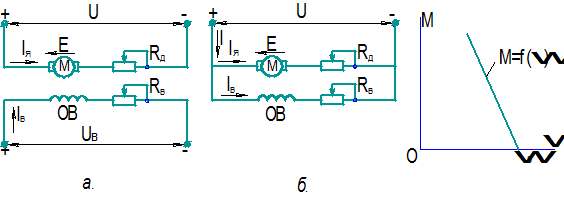
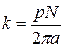 (р - число пар полюсов; N - число активных проводников обмотки якоря; а – число пар параллельных ветвей обмотки якоря); Ф, w – соответственно магнитный поток и угловая скорость двигателя.
(р - число пар полюсов; N - число активных проводников обмотки якоря; а – число пар параллельных ветвей обмотки якоря); Ф, w – соответственно магнитный поток и угловая скорость двигателя.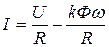 . (2.3)
. (2.3)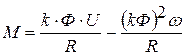 (2.5)
(2.5)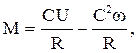 (2.6)
(2.6)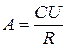 ;
; 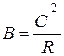 - постоянные коэффициенты.
- постоянные коэффициенты.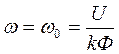 . (2.8)
. (2.8)