|
|
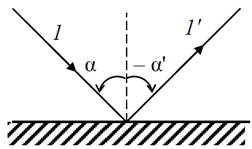
Идеальная оптическая системаГеометрическая оптика Предмет геометрической оптики Под геометрической оптикой понимают раздел оптики, в котором при решении оптических задач пренебрегают волновыми свойствами света. Так предполагается, что: - длина волны света пренебрежимо мала, - поляризация света не учитывается, - амплитудой волны можно пренебречь. Таким образом, этот метод имеет значительные ограничения или не применим вообще в случаях, когда нельзя пренебречь волновыми свойствами света. Основной задачей геометрической оптики является нахождение траекторий распространения лучей света в среде, траекторий лучей после отражения или прохождения границ раздела сред с целью построения изображения предмета. Основные законы геометрической оптики Законы геометрической оптики были установлены экспериментально. Закон прямолинейного распространения света «В однородной среде свет распространяется вдоль прямой линии». Этот закон нарушается в случаях, когда становятся существенными дифракционные эффекты. Закон независимости световых пучков «Световые лучи распространяются независимо друг от друга», т.е. не оказывают никакого влияния друг на друга. Этот закон нарушается в случаях, когда необходимо учитывать явления интерференции и зависимости оптических свойств среды от интенсивности света. Закон отражения от поверхности «Падающий луч, отраженный луч и нормаль к поверхности лежат в одной плоскости, а угол, под которым свет отражается от поверхности, равен по величине углу, под которым свет падает на эту поверхность». Угол отсчитывается от нормали к поверхности против часовой стрелки.
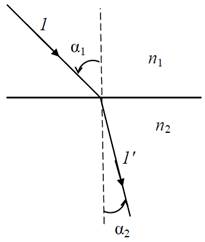
Рис. 1. Падающий луч – 1, отраженный луч – 1' Математически этот закон выражается формулами: -a' = a или |a' | =|a| (1) Закон преломления на границе раздела двух сред (Закон Снелла) «Падающий луч, преломленный луч и нормаль к поверхности раздела лежат в одной плоскости, а произведение показателя преломления среды на синус угла между нормалью не меняется при переходе через границу раздела двух сред».
Рис. 2. Падающий луч – 1, преломленный луч – 1' Математически этот закон выражается следующей формулой: n1sina1 = n2sina2 (2) Под показателем преломления среды n понимают отношение скорости света в вакууме – c к скорости света в среде – v: n = Из (2), с учетом знаков углов, для закона отражения должно выполняться равенство n1×sina = - n2 sina' , откуда следует: n1 = - n2. (4) Таким образом, результаты, полученные для преломления на поверхности можно применить для рассмотрения случая отражения сделав замену (4). Из уравнения (2) следует, что при n1 < n2 угол преломления меньше угла падения a1 > a2. В случае, когда n1 > n2, т.е. в случае падения света из оптически более плотной среды на границу среды с меньшей оптической плотностью, угол преломления больше угла падения a1 < a2. При угле падения a0 = arcsin Закон взаимности (Обратимости хода лучей) «При изменении направления распространения света в лучах на противоположное их взаимное расположение не меняется». То есть, при изменении направления стрелок на рисунках в законах отражения и преломления положения лучей не меняются. Фактически этот закон фиксирует тот факт, что распространение света между двумя точками в пространстве всегда происходит по одному и тому же пути, независимо от направления. Этот закон нарушается в случаях, когда требуется учитывать поляризацию света. Принцип Ферма Законы геометрической оптики, касающиеся направления лучей, как оказалось позднее, являются следствием принципа, установленного итальянским математиком Ферма: «Свет между двумя точками распространяется по пути, требующему наименьшего времени, в сравнении с любыми другими путями между этими точками». В настоящее время этот принцип формулируется следующим образом: «Путь, по которому распространяется свет, соответствует экстремуму времени распространения». Это означает, что время распространения по этому пути может быть как минимальным, так и максимальным или равным в сравнении со временем при распространении по всем другим возможным путям. Вывод законов геометрической оптики из принципа Ферма приведен ниже, чтобы прояснился смысл фразы «экстремум времени распространения». Закон прямолинейного распространения. Действительно, закон прямолинейного распространения света тривиальным образом следует из принципа Ферма, поскольку в однородной среде скорость распространения не меняется, то наименьшее время для прохождения между двумя точками будет иметь место при движении по наикратчайшему пути, т.е. вдоль прямой линии (показано стрелкой), соединяющей эти точки. Рис. 3. Из всех возможных траекторий (показаны штриховой линией) в однородной среде луч света пойдет по наикратчайшему пути АВ Закон отражения.Закон отражения выводится также как и в предыдущем случае, только с учетом того, что на отражающей поверхности происходит излом траектории. Действительно, из точки А в точку В можно попасть при отражении от любой точки поверхности. Возьмем на поверхности точку C, соответствующую отражению под тем же углом, под которым происходит падение, и любую точку D, от которой отражение происходит под углом не равным углу падения. Точка В' является отражением точки B относительно плоскости, т.е. расстояния от этих точек до плоскости равны. Из рисунка видно, что |CB| = |CB'| и |DB| = |DB'|, но тогда |АСВ| = |АСВ'| и |АDB| = |АDВ'|. Из рисунка видно, что |ACB'| < |ADB'|, и, следовательно, время на прохождение пути |АСВ| будет наименьшим. Таким образом, отраженный луч будет двигаться вдоль направления, которое составляет с нормалью угол, равный углу падения.
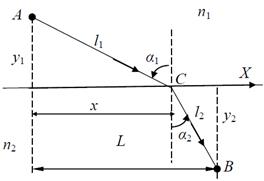
Рис. 4. Если зеркально отразить точку B относительно поверхности, то прямая AB' пересечет поверхность в точке, в которой будет выполняться закон отражения Закон преломления. Чтобы получить закон преломления из принципа Ферма, рассмотрим распространение света из точки A в точку B, находящиеся в средах с показателями преломления n1 и n2 , соответственно. Надо найти положение точки C на границе раздела, для которой выполняется принцип Ферма. Введем декартову систему координат как показано на рисунке. Тогда положение точки C будет зависеть только от координаты x. Тогда экстремум времени распространения между точками A и B определяется из равенства нулю производной Это время складывается из времен распространения в каждой из сред: t = t1 + t2, где t1 =
Из последнего равенства следует закон Снелла (2).
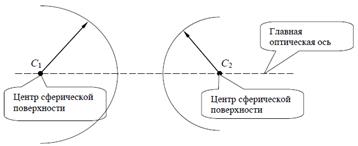
Рис. 5. Траектория распространения света из A в B, если эти точки находятся в средах с разными показателями преломления. В точке С должен выполняться закон преломления Принцип Ферма позволяет получать траекторию распространения света и в неоднородной среде. Например, из последнего рисунка видно, что если показатель преломления во второй среде будет увеличиваться с удалением от границы раздела, то угол преломления с удалением от поверхности будет уменьшаться, т.е. преломленный луч света в такой среде будет распространяться вдоль некоторой кривой. Основные понятия и приближения геометрической оптики С помощью законов геометрической оптики можно построить изображение предмета, получаемое любой оптической системой, в которой можно пренебречь волновыми свойствами света. Для этого каждую точку предмета, считают источником света и находят положение ее изображения после прохождения оптической системы. Совокупность изображений точек предмета дает изображение всего предмета. Но в общем случае сложной оптической системы построение изображения связано с громоздкими вычислениями, поэтому вводят ряд приближений, упрощающих построение. Под оптической системой здесь понимается набор чередующихся преломляющих или отражающих сферических поверхностей. Плоская поверхность является частным случаем сферической поверхности с радиусом R = ∞. Предполагается в дальнейшем, что все центры сферических поверхностей, которые составляют систему, лежат на одной прямой, которую называют главной оптической осью. В этом случае говорят, что система центрирована.
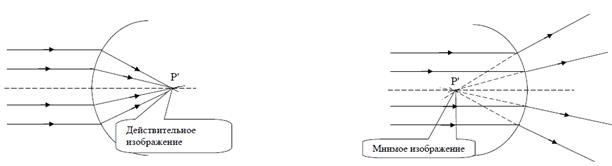
Рис. 6. Центрированная система, состоящая из двух сферических преломляющих поверхностей различного радиуса. Центры поверхностей обозначены как C, они находятся на одной прямой, называемой главной оптической осью В дальнейшем предполагается, что пучок света от источника состоит из приосевых лучей, т.е. лучей отклоняющихся на небольшой угол от главной оптической оси, для них тогда угол падения на преломляющую поверхность можно также считать малым. Пучок таких лучей называют параксиальным. Если лучи света, составляющие пучок, исходят из одной точки, то такой пучок называют гомоцентрическим. Частный случай гомоцентрического пучка – пучок параллельных лучей, в этом случае считается, что их источник находится в бесконечности. Если изображением любой точки предмета является также точка, то в этом случае говорят, что изображение стигматическое или точечное. Оптическая система, дающая стигматическое изображение, называется идеальной. Различают действительные и мнимые изображения. Действительное изображение – изображение, получившееся в результате пересечения лучей, прошедших через систему. Мнимое изображение – изображение, получившееся в результате пересечения продолжений лучей, прошедших через систему, в направлении, обратном распространению света.
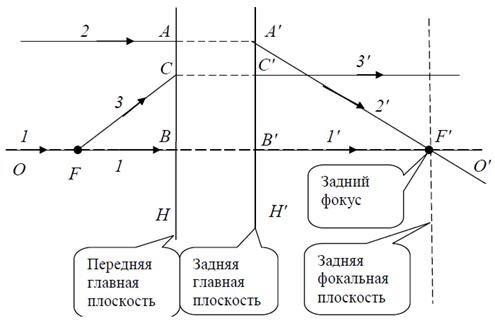
Рис. 7. На первом рисунке показано действительное изображение, полученное пересечением преломленных лучей, на втором рисунке мнимое изображение, полученное пересечением продолжений лучей, преломленных на сферической поверхности Точка P, в которой находится источник, и точка P', в которой получается его изображение, называют сопряженными точками, так как согласно закону взаимности их можно поменять местами, т.е. источник в точке P' даст изображение в точке P. Таким образом, оптическую систему можно рассматривать как систему, осуществляющую взаимно однозначное преобразование точек предмета в точки изображения. Идеальная оптическая система Общую теорию идеальных оптических систем развил немецкий математик и физик Гаусс на основе представления об оптической системе как некотором преобразовании точек предмета (еще говорят – пространства предметов) в точки изображения (пространство изображений). Поскольку в идеальной оптической системе точка в пространстве предметов преобразуется в единственную сопряженную точку в пространстве изображения, то прямая, в пространстве предметов должна преобразовываться в сопряженную прямую в пространстве изображений, при этом порядок следования трех точек на прямой в пространстве предметов в пространстве изображения не меняется. То есть идеальная оптическая система, из какого бы числа преломляющих поверхностей она не состояла, осуществляет только преобразование подобия и тогда эту систему можно рассматривать формально, пользуясь некоторыми правилами преобразования точек предмета в точки изображения. Для этого введем две параллельные плоскости H и H', перпендикулярные главной оптической оси системы. Для этих плоскостей должно выполняться следующее условие: отрезок ВА на первой плоскости преобразуется оптической системой в отрезок В'A' второй плоскости без изменения длины отрезка, т.е. для этих плоскостей коэффициент подобия V = 1, и для любой точки А плоскости H сопряженная ее точка A' на плоскости H' получается переносом точки А до H' параллельно главной оптической оси. Эти плоскости называют главными. Плоскость H на которую падает свет из пространства объектов называют первой (или передней). Все расстояния в плоскости предметов отсчитываются от этой плоскости, а все расстояния в плоскости изображения отсчитываются от второй (задней) плоскости H'. Поэтому их и назвали главными. При отсчитывании расстояний используют правило знаков: если отсчет расстояния ведется против направления распространения света, то эти расстояния берутся со знаком «–», если отсчет ведется по направлению распространения света, то эти расстояния берутся со знаком «+». Поскольку система идеальная, т.е. гомоцентрическая точка в пространстве предметов переходит в гомоцентрическую точку в пространстве изображения, то справедливы следующие два правила преобразования лучей в оптической системе: 1. Источник на бесконечности, лучи от которого идут параллельно оптической оси (лучи 1 и 2 до плоскости H), преобразуется системой в точку F' (получаемую пересечением сопряженных лучей 1' и 2' после плоскости Н’) на оптической оси. Точка F' называется задним фокусом. Расстояние |B'F'| = B'F' называют задним фокусным расстоянием. Плоскость, проходящая через точку F', перпендикулярная главной оптической оси, называется задней фокальной плоскостью. 2. На главной оптической оси существует точка F, из которой свет источника (лучи 1 и 3) после задней главной плоскости распространяется параллельно оптической оси (лучи 1' и 3'), т.е. преобразуется в точечное изображение, находящееся в бесконечности. Точка F называется передним фокусом. Расстояние |BF| = – BF называют передним фокусным расстоянием (знак минус перед BF появился по правилу знаков). Плоскость, проходящая через точку F, перпендикулярная главной оптической оси, называется передней фокальной плоскостью.
Рис. 8. Построение изображения в идеальной оптической системе: лучи 1 и 2, параллельные главной оптической оси, пересекутся в заднем фокусе системы F'; лучи 1 и 3, выходящие из фокуса F, после задней главной плоскости распространяются параллельно главной оптической оси 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (3)
. (3) , угол преломления становится равным 90° и при дальнейшем увеличении угла падения преломленного луча уже не существует. Эффект отсутствия преломленного луча называют полным внутренним отражением, а угол a0 наименьшим углом полного внутреннего отражения.
, угол преломления становится равным 90° и при дальнейшем увеличении угла падения преломленного луча уже не существует. Эффект отсутствия преломленного луча называют полным внутренним отражением, а угол a0 наименьшим углом полного внутреннего отражения.

 = 0, где t – время распространения между точками A и B.
= 0, где t – время распространения между точками A и B.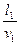 =
=  =
=  , а t2 =
, а t2 =  =
=  =
=  . Найдем производную и приравняем ее нулю:
. Найдем производную и приравняем ее нулю: -
-  =
= 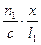 -
- 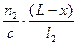 =
=  sina1 -
sina1 -  sina2 = 0.
sina2 = 0.