
|
|
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ И ПРИНЦИП ГАУССА12 Принцип Гаусса позволяет свести получение дифференциальных уравнений движения к выписыванию условий экстремума принуждения (6), являющегося функцией второй степени относительно ускорений. Рассмотрим пример.
Функция Z вычисляется по формуле
Так как Fx = mg, Fy = 0, а
То она может быть записана в виде
Из условия При помощи принципа Гаусса были найдены новые уравнения аналитической динамики, применимые к системам как с геометрическими, так и с дифференциальными неинтегрируемыми связями (последние системы называются неголономными). Это уравнения Гиббса-Аппеля, широко используемые, например, в динамике твердых тел, катящихся без скольжения по неподвижной или подвижной поверхности. ЗАКЛЮЧЕНИЕ Принцип наименьшего принуждения Гаусса исследовали многие математики, механики и физики. Для целей разного рода теоретических исследований и решения конкретных задач принципу были даны различные модификации и обобщения. В XIX веке благодаря трудам Г. Шеффлера, А. Риттера, Р. Липшица, Дж. Гиббса, Л. Больцмана и др. была получена аналитическая формулировка принципа Гаусса, уточнен характер варьирования движения, дано применение принципа к системам с неудерживающими связями, обнаружилось значение принципа Гаусса как наиболее общего принципа механики. Еще более существенное развитие принцип Гаусса получил в нашем столетии. Исследования А. И. Грдины развивали принцип Гаусса вообще и особенно применительно к динамике живых организмов. В его работах впервые рассмотрены связи, зависящие от переменных параметров, показано, что принцип Гаусса распространяется на неголономные системы с “волевыми связями”. Е.А. Болотов обобщил принцип Гаусса на случай частичного освобождения систем от голономных и линейных по скоростям неголономных связей, расширив тем самым высказанную еще Э. Махом мысль о частичной освобождаемости в случае голономных связей. (У Гаусса все связи удерживающие и предполагается полное освобождение системы.) Обобщенный принцип Гаусса в формулировке Болотова состоит в том, что отклонение действительного движения системы от действительного же ее движения, получающегося при отбрасывании всех неудерживающих связей и произвольного числа удерживающих, меньше, чем отклонение любого из возможных движений. Е.А. Болотов также показал справедливость обобщенного принципа Гаусса в некоторых задачах теории удара. Совсем недавно В.А. Синицын получил новую форму принципа Гаусса, предполагающую освобождение системы не от всех (как у Болотова), а только от части неудерживающих связей. Эта новая форма принципа Гаусса была применена Синицыным при анализе проблемы ослабления неудерживающих связей. Н.Г. Четаев дал новое (аксиоматическое) определение понятия виртуального перемещения для неголономных систем с нелинейными по скоростям связями. Он также предложил новую точку зрения на освобождение материальных систем. Че- таев показал, что при данном им определении виртуальных перемещений и освобождении принцип Гаусса справедлив и для нелинейных неголономных систем. Кроме того, Четаев дал новую энергетическую трактовку принципа Гаусса для систем с голономными и линейными неголономными связями. В последние десятилетия принцип Гаусса получил дальнейшее развитие в работах В.В. Румянцева. Он установил принцип Гаусса для систем с неидеальными связями, обобщил его на сплошные среды, на управляемые механические системы. Принцип наименьшего принуждения имеет не только теоретическую, но и большую практическую значимость. Область его приложений не ограничивается только задачами механики. Этот принцип находит приложения в теоретической физике и других смежных областях естествознания. Недавно Б. Вуяновичем (B. Vujanovic, 1976) принцип Гаусса был использован для получения приближенных решений дифференциальных уравнений (обыкновенных и в частных производных). Предложен компьютерный метод моделирования динамики сложных управляемых многозвенных механических систем без вывода уравнений движения на основе прямой реализации принципа наименьшего принуждения Гаусса (А.Ф. Верещагин, 1975). Принцип Гаусса и сейчас привлекает внимание исследователей, теоретиков и прикладников. В самом выражении “наименьшее принуждение” заключена какая-то неразгаданная тайна. Как и почему природа минимизирует принуждение? Наверное, на этот вопрос нет ответа. Возможности же практического использования идей, содержащихся в принципе наименьшего принуждения Гаусса, в прикладных задачах раскрыты далеко не полностью. Поиск продолжается...
Литература 1.Гаусс, К. Об одном новом общем принципе механики.Вариационные принципы механики. М. : Физ-матгиз, 1959: – С. 170-172с. 2.Четаев, Н.Г. Устойчивость движения.Работы по аналитической механике. М. : Изд-во АН СССР, 1962: – 535с. 3.Цыганова,Н.Я.Основные этапы развития принципа наименьшего принуждения.История и методология естественных наук. М. : Изд-во МГУ, 1970: - 122-134с. 4.Румянцев, В.В.О принципах Гаусса и Четаева для систем с неидеальными связями.Теоретическая и прикладная механика. 1974: – Т. 5, № 1.9-14с. 5.Синицын, В.А.О принципе наименьшего принуждения для систем с неудерживающими связями.Прикл. математика и механика. 1990: – Т. 54, вып. 6. 920-925с. 6.Маркеев, А.П. Теоретическая механика. М. : Наука, 1990: – 416с. 7. Веретенников, В.Г. Теоретическая механика: Дополнения к общим разделам / В. А. Синицын – М. : МАИ, 1996: – 340с.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Пример 6. Найдем дифференциальное уравнение плоского движения математического маятника. Маятник представляет собой точечную массу, прикрепленную при помощи невесомого стержня длины l к точке O, около которой стержень может вращаться без трения в вертикальной плоскости (рис. 4).
Пример 6. Найдем дифференциальное уравнение плоского движения математического маятника. Маятник представляет собой точечную массу, прикрепленную при помощи невесомого стержня длины l к точке O, около которой стержень может вращаться без трения в вертикальной плоскости (рис. 4).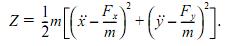
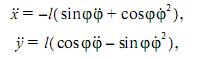
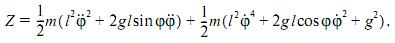
 получаем искомое уравнение
получаем искомое уравнение