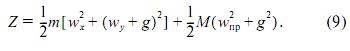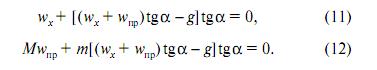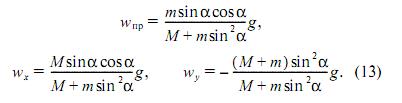|
|
ФОРМУЛИРОВКА ПРИНЦИПА НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ12 ВСПОМОГАТЕЛЬНЫЕ СВЕДЕНИЯ Для формулировки принципа Гаусса следует предварительно дать необходимые определения и понятия из теоретической механики. Рассмотрим систему материальных точек Pv, v = 1, 2, ..., N, с массами mv, радиусы-векторы и прямоугольные декартовы координаты которых в неподвижной системе координат обозначим через rv и xv, yv, zv, через vv и wv обозначим скорость и ускорение точки Pv. Очень часто при движении системы положения и скорости ее точек не могут быть произвольными. Ограничения, налагаемые на rv и vv, , которые должны выполняться при любых действующих на систему силах, называются связями. Если на систему не наложены связи, то она называется свободной. Системы со связями называют несвободными. В общем случае связь задается соотношением f(ru ..., rn, Vj, ..., vn, t) > 0. Если в нем реализуется только знак равенства, то связь называется удерживающей. Например, при движении точки P по сфере постоянного или переменного радиуса R с центром в начале координат имеем удерживающую связь x2 + y2 + z2 - R2 = 0. Если же в соотношении f > 0 реализуются как знак равенства, так и знак строгого неравенства, то связь называется неудерживающей. Пусть, например, две точки Р1 и Р2 связаны нерастяжимой нитью длины l. Здесь имеем неудерживающую связь, задаваемую соотношением l2 – (xJ – x2)2 – (yx – y2)2 – (z1 – z2)2 ≥ 0, которое означает, что точки не могут находиться одна от другой на расстоянии, большем l. Если соотношение, задающее связь, не содержит проекции скоростей точек системы, то эта связь называется геометрической (или голономной), в противном случае связь называется дифференциальной. Иногда дифференциальную связь можно представить в виде зависимости между координатами точек системы и временем (как в случае геометрической связи). Тогда ее называют интегрируемой. Неинтегрируемую дифференциальную связь называют еще неголономной. Точки несвободной системы не могут двигаться в пространстве совершенно произвольно. Их кинематически возможные (то есть допускаемые связями) координаты, скорости, ускорения и перемещения должны удовлетворять некоторым соотношениям, вытекающим из уравнений связей. Помимо перемещений, соответствующих действительному (истинному, реальному) движению, в механике важны еще так называемые виртуальные (воображаемые) перемещения. Виртуальным перемещением точки Р, называют такое ее малое перемещение Поясним это на примере. Рассмотрим систему, состоящую из одной материальной точки, которая должна оставаться на поверхности f(x, y, z, t) = 0. Пусть в момент времени t точка занимает положение P0 с координатами x0, y0, z0. Мысленно дадим точке бесконечно малое перемещение
где частные производные вычисляются в точке P0, а многоточие обозначает члены выше первого порядка малости относительно
определяющему виртуальные перемещения. Уравнение (1), в частности, показывает, что в отличие от действительного перемещения, которое единственно, число виртуальных перемещений бесконечно: мы имеем одно линейное уравнение (1) относительно трех неизвестных Бесконечно малые приращения Если система свободная, то ускорения av ее точек определяются из второго закона Ньютона: mv av = Fv, где Fv — равнодействующая сил, приложенных к точке Pv. Если же система несвободная, то на ускорения ее точек наложены вполне определенные ограничения. Величины av не будут, вообще говоря, удовлетворять этим ограничениям, то есть ускорения wv точек Pv несвободной системы будут отличаться от их ускорений av в случае свободной системы, у точки Pv появляется дополнительное ускорение wv - av. Это ускорение возникает за счет неизвестных сил, обусловленных наличием связей. Их называют реакциями связей. Силы Fv называют активными силами. Они являются известными функциями координат и скоростей точек системы, а также, возможно, и времени t. Обозначив через Rv равнодействующую реакций связей, приложенных к точке Pv, согласно второму закону Ньютона получим mv (wv - a) = Rv. Отсюда и из равенств mv av = Fv следуют уравнения движения точек системы mvwv = R + Fv, v = 1, 2, …, N. Связи называются идеальными, если работа реакций этих связей на любых виртуальных перемещениях равна нулю, то есть
Примерами систем с идеальными связями могут служить следующие системы: материальная точка на абсолютно гладкой поверхности; свободное твердое тело; тело, вращающееся вокруг неподвижной оси; два тела, соединенные точечным шарниром; два соприкасающихся тела при отсутствии проскальзывания; две точки, соединенные невесомой нерастяжимой нитью, не оказывающей сопротивления изменению ее формы (идеальная нить). Многие материальные объекты в природе и технике с приемлемой для практики точностью можно моделировать системой с идеальными связями. Далее рассматриваются только такие системы.
ФОРМУЛИРОВКА ПРИНЦИПА НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ Принцип наименьшего принуждения дает признак, отличающий действительное движение от класса других движений, кинематически возможных при тех же условиях. Гаусс дал следующую словесную формулировку своего принципа: “Движение системы материальных точек, связанных между собой произвольным образом и подверженных любым влияниям, в каждое мгновение происходит в наиболее совершенном, какое только возможно, согласии с тем движением, каким обладали бы эти точки, если бы все они стали свободными, то есть происходит с наименьшим возможным принуждением, если в качестве меры принуждения, примененного в течение бесконечно малого мгновения, принять сумму произведений масс каждой точки на квадрат величины ее отклонения от того положения, которое она заняла бы, если бы была свободной”. Пусть Pv — положение v-й точки в момент времени t (рис. 1), а Bv — положение, которое заняла бы эта точка через промежуток времени dt, если бы в момент t система была освобождена от связей. Приведенный принцип утверждает, что положения A, которые займут точки системы в момент t + dt в действительном движении, выделяются между всеми положениями, допускаемыми связями, тем, что для них величина G, определяемая по формуле
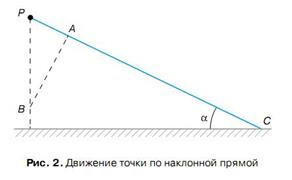
где sv — длина вектора BVAV, имеет минимальное значение. Таким образом, мерой принуждения Гаусс называет величину (4), характеризующую отклонение системы, движущейся под действием активных сил при наложенных на нее связях, от свободного движения, которое она имела бы начиная с рассматриваемого момента, двигаясь под действием тех же активных сил, с теми же начальными скоростями в момент времени t, если бы с этого момента были устранены наложенные на систему связи. Равновесие является частным случаем движения и также описывается принципом Гаусса. Пусть система занимает некоторое допускаемое связями положение и все ее точки имеют нулевые скорости. Тогда если каждое движение дает большее значение величине (4), то рассматриваемое положение будет положением равновесия. В этом случае состояние покоя является более близким к свободному движению, нежели любое кинематически возможное движение. Весьма интересно, что идея отклонения системы от свободного движения в форме (4) суммы величин, пропорциональных квадратам отклонений точек системы, заимствована Гауссом в им же построенной теории ошибок. Принцип наименьшего принуждения является механическим аналогом метода наименьших квадратов, лежащего в основе всех статистических исследований. Величина (4), будучи поделенной на массу всей системы, выразит квадрат среднего взвешенного из квадратов отклонений отдельных точек системы, причем множители mv соответствуют “весовому” множителю в методе наименьших квадратов. Выявляя замечательную внутреннюю связь идеи принципа наименьшего принуждения с методом наименьших квадратов, Гаусс замечает, что “свободное движение, если оно при наличии имеющихся условий не может иметь места, модифицируется природой в точности таким образом, каким вычисляющий математик, пользуясь методом наименьших квадратов, выравнивает результаты эксперимента, относящиеся к величинам, связанным некоторой зависимостью”. Следующий пример иллюстрирует принцип Гаусса Пример 1. Материальная точка движется под действием силы тяжести по гладкой прямой, наклоненной к горизонтальной плоскости под углом а (рис. 2). Найдем ускорение точки. Пусть в начальный момент точка занимает положение P и имеет скорость, равную нулю. При свободном движении точка двигалась бы по вертикали и за время dt прошла бы расстояние PB = 1/2 g(dt)2. В действительном несвободном движении по прямой PC точка движется с неизвестным ускорением w и за время dt проходит расстояние PA = 1/2 w(dt)2. Действительное движение наименее отклонится от свободного движения, если точка A будет основанием перпендикуляра, опущенного из точки B на прямую PC. Следовательно, PA = PB sin а. Отсюда с учетом выражений для PA и PB находим искомое ускорение: w = gsin а.
 Для применения принципа Гаусса к решению конкретных задач механики и физики целесообразно получить его аналитическое выражение в декартовых координатах. Пусть в момент времени t точка Pv несвободной системы имеет скорость vv, а Fv — равнодействующая всех активных сил, приложенных к точке Pv. Тогда (см. рис. 1) с точностью до членов второго порядка малости относительно dt имеем Для применения принципа Гаусса к решению конкретных задач механики и физики целесообразно получить его аналитическое выражение в декартовых координатах. Пусть в момент времени t точка Pv несвободной системы имеет скорость vv, а Fv — равнодействующая всех активных сил, приложенных к точке Pv. Тогда (см. рис. 1) с точностью до членов второго порядка малости относительно dt имеем
Отклонение sv = BVAV точки Pv при несвободном движении от ее положения при свободном движении вызвано действием связей, принуждающих точки системы отклоняться от движения, свойственного точкам свободной системы. Для квадрата длины вектора sv получаем выражение
и функция (4), следовательно, может быть записана в виде G = 1/2(dt)4Z, где
Функция Z называется принуждением (по-немецки Zwang). От меры принуждения (4) она отличается несущественным для существования экстремума множителем 1/2(dt)4. Отбрасывая этот множитель, получаем следующую формулировку принципа Гаусса: в каждый момент времени истинное движение системы, находящейся под действием активных сил и подверженной идеальным удерживающим связям, отличается от всех кинематически возможных движений, совершающихся из той же начальной конфигурации и с теми же начальными скоростями, тем свойством, что для истинного движения принуждение Z является минимальным. Математически это выражается равенством δZ = 0, причем вариация берется при неизменяемых координатах и скоростях точек системы, то есть варьируются только ускорения. В координатной форме принуждение записывается в виде
Рассмотрим несложный пример применения принципа наименьшего принуждения к решению задач механики. Пример 2. Три груза массы m каждый соединены невесомой нерастяжимой нитью, переброшенной через неподвижный блок (рис. 3, а). Два груза лежат на горизонтальной плоскости, а третий груз подвешен вертикально. Пренебрегая трением, найдем ускорения грузов.
Так как нить нерастяжима, то грузы движутся с одинаковыми по модулю ускорениями. Имеем w1 = w2 = wj, w3 = wi; F1 = F2 = F3 = mgi. Для принуждения (7) получаем
Функция Z является квадратным трехчленом относительно w. Из условия его минимума получаем w = = 1/3 g. Следующий пример иллюстрирует применимость принципа Гаусса к случаям равновесия. Пример 3. К концам невесомого горизонтального рычага с плечами l1 и l2 подвешены грузы P1 и P2 весами m1 g и m2g соответственно (рис. 3, б). Вначале система удерживалась в покое. Когда ее отпускают, грузы могут прийти в движение. В самом начале движения ускорения грузов будут вертикальны. Пусть ускорение w1 груза P1 равно w и направлено вниз. Тогда, очевидно, ускорение w2 груза P2 направлено вверх и равно w(l2/11). Для принуждения Z имеем выражение
Из условия минимума функции Z находим
Если веса грузов обратно пропорциональны плечам рычага, то есть m1 /m2 = l2/11, то w = 0 и рычаг находится в равновесии. В этом случае, следовательно, покой дает наименьшее отклонение от свободного движения. Теперь используем принцип Гаусса для решения несколько более сложных задач. Пример 4. Дана система из двух блоков, неподвижного A и подвижного B и трех грузов P1, P2, P3, подвешенных при помощи невесомых нерастяжимых нитей, как показано на рис. 3, в. Массы грузов соответственно равны m1, m2, m3, блоки невесомы, трения нет. При t = 0 скорости грузов равны нулю. При каком соотношении масс грузов груз P1 при t > 0 будет опускаться? Пусть x1, x2, x3 — координаты грузов P1, P2, P3, а xB — координата центра блока B. Тогда
а условия нерастяжимости нитей запишутся в виде равенств x1 + xB = const, x2 + x3 - 2xB = const. Отсюда получаем, что
Выразив
Из условий экстремума имеем два уравнения для нахождения ускорений
или (m1+4m3) 2m3 Из этих уравнений находим
Груз P1 будет опускаться, если
Пример 5. Призма А массы m скользит по боковой грани призмы B массы М, образуя угол α с горизонтом (рис. 3, г). Определить ускорение wпр призмы B и горизонтальную wx и вертикальную wy составляющие ускорения призмы А. Трением пренебречь. Так как призма А не отрывается от призмы B, то (см. рис. 3, г) wx = –wпр + wотн Для принуждения имеем выражение
Но из (8) следует, что wy = –(wx + wпр)tgα. (10) Поэтому Условие экстремума
дают уравнения
Из системы уравнений (10) – (12) получаем искомые величины:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 rv = (
rv = ( 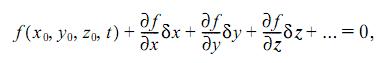
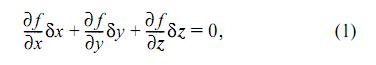


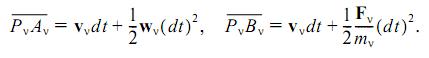
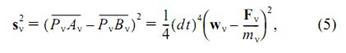
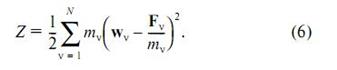
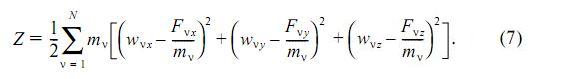

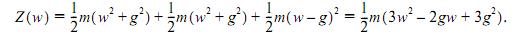
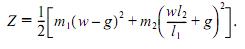
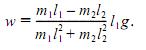
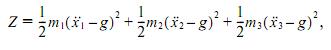
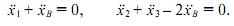
 3 получим, что функция Z будет функцией от двух переменных
3 получим, что функция Z будет функцией от двух переменных 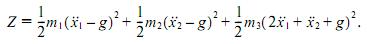
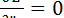
 +2m3
+2m3 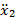 = (m1 – 2m3)g
= (m1 – 2m3)g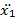 + (m2 + m3)
+ (m2 + m3) 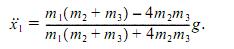
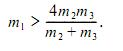
 , wy = –wотн
, wy = –wотн  . (8)
. (8)