
|
|
Гидравлическое уравнение количества движения для установившегося потокаВозьмем поток произвольной формы (рис. 3-38, а), наметим два живых сечения 1—1 и 2—2, покажем произвольную ось х. Поставим себе цель привести известную из теоретической механики теорему о количестве движения материальных точек к виду, удобному для расчета установившегося движения жидкости, когда в районе живых сечений 1—1 и 2—2 (рис. 3-38, а) имеет место плавно изменяющееся движение. Дополнительно будем считать, что распределения скоростей и в сечениях 1—1 и 2—2 примерно одинаковы, а поэтому можно считать, что
Рис. 3-38. К обоснованию гидравлического уравнения количества движения Напомним, что упомянутая теорема читается так: проекция на произвольно намеченную ось к приращения количества движения
Применим эту теорему к отсеку жидкости АВ, заключенному в начальный момент времени между сечениями /—1 и 2—2 и перемещающемуся за время dt в положение А'В'. 1°. Приращение количества движения [ Очевидно,
Известно, что количество движения (КД) тела равно КД = массе тела X скорость тела. Имея это в виду, найдем количества движения объемов жидкости 8Уг и 8V2, т. е. величины КД
Если бы все жидкие частицы этой массы проходили через живое сечение 1—1 с одинаковой скоростью v1 то количество движения
Так как в различных точках сечения 1—1 в действительности имеем разные скорости и, то согласно (3-87) искомое количество движения должно записаться в виде:
где vx — средняя скорость в живом сечении 1—1. Для величины
где v2 — средняя скорость в живом сечении 2—2. Подставив (3-117) и (3-118) в (3-114) и заменив v1 и v2 проекциями этих векторов на ось х, т. е. величинами v1x и v2x, получаем:
2°. Импульсы сил (ИС), приложенных к телу АВ. Известно, что импульс силы ИС = силе Рассмотрим все внешние силы, действующие на жидкое тело АВ при перемещении его в положение А'В'. Сила собственного веса тела АВ. Обозначим эту силу через G и ее проекцию на ось х через Gx. Проекция импульса этой силы равна Gx dt. (3-120) Сила внешнего трения Т0, приложенного к боковой поверхности жидкого тела АВ со стороны боковых стенок, ограничивающих это тело. Проекция импульса этой силы равна (Т0)х dt, (3-121) где (Т0)х — проекция данной силы на ось х. Сила реакции боковых стенок, ограничивающих жидкое телоЛВ (без учета сил трения, рассмотренных выше). Проекция импульса этой силы равна Rxdt, (3-122) где R* — проекция данной силы на ось х. Сила гидродинамического давления, действующего на торцовые сечения жидкого тела АЕ (на сечения 1—1 и 2—2) со стороны остальной жидкости (см. на чертеже силы Р1 и Ра). Проекция импульса этих двух сил ( где Рх — сумма проекций на ось х указанных двух сил. 3°. Гидравлическое уравнение количества движения. Подставляя в (3-113 выражения (3-119)—(3-123) и деля полученный результат на dt, искомое уравнение получаем в виде
где Проекции сил и скоростей, направленных против оси х, должны иметь з уравнении (3-124) отрицательную величину. Гидравлическое уравнение количества движения (3-124) — уравнение баланса секундного количества движения — можно прочесть так: при переходе от плоского живого сечения 1—1 к плоскому живому сечению 2—2 проекция (на какую-либо ось) секундного количества движения потока изменяется на величину, равную сумме проекций на ту же ось всех четырех внешних сил (G, T0, R, Р), действующих на отсек потока, заключенный между сечениями 1—1 и 2—2.
Рис. 3-39. Давление горизонтальной струи на вертикальную плоскую стенку Из сказанного ясно, что векторы всех внешних сил, действующих на рассматриваемый отсек жидкости (см. силы G, R, Т0, Р1 и Р2 на рис. 3-38, а), вместе с векторами секундного количества движения ( 4°. Пример использования уравнения количества движения. Уравнением (3-124) удобно пользоваться при решении различных практических задач Для примера рассмотрим случай, когда струя, выходящая из круглоцилиндрического сопла А, ударяется о плоскую стенку В, расположенную нормально к ней (рис. 3-39). Как видно, здесь (при достаточно больших скоростях истечения жидкости) получаем так называемую осесимметричную задачу растекания потока по стенке В. Живое сечение 2—2, показанное на чертеже, имеет круглоцилиндрическую форму: на вертикальную плоскость, нормальную к чертежу, контур этого сечения проектируется в окружность, причем линии тока пересекают такую окружность в радиальном направлении. Данный случай может рассматриваться как исключение: несмотря на наличие криволинейного живого сечения 2—2 и резко изменяющегося движения жидкости в нем, мы все же, рассматривая такое сечение, можем пользоваться понятием средней скорости, а следовательно, и уравнением (3-124). Чтобы найти давление Р0 струи на стенку В, намечаем ось х, как показано на чертеже, и затем выделяем сечениями 1—1 и 2—2 отсек жидкости, к которому и прилагаем уравнение (3-124). 1. Изменение проекции секундного количества движения при переходе от сечения 1—1 к сечению 2—2
Обычно насадку А делают несколько сходящейся по течению. При этом распределение скоростей и в сечении 1—1 оказывается весьма близким к равномерному (когда 2. Проекции на ось х сил, действующих на рассматриваемый отсек: Gx = 0;
3. Как видно, согласно уравнению (3-124), получаем: —pQvi = — Р0, откуда искомая сила давления струи на преграду P0 = pQv1 = Или 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (3-112)
(3-112)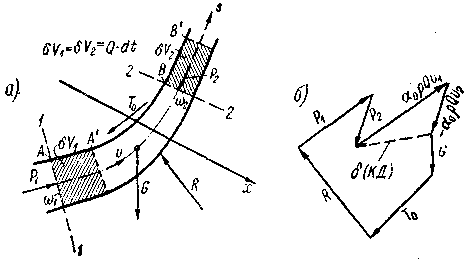
 (КД) движущегося тела равна сумме проекций на ось х импульсов внешних сил (ИС), действующих на тело, за соответствующий промежуток времени. Данную теорему условно можно написать в виде:
(КД) движущегося тела равна сумме проекций на ось х импульсов внешних сил (ИС), действующих на тело, за соответствующий промежуток времени. Данную теорему условно можно написать в виде: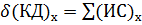 (3-113)
(3-113) (ЛТД)] тела АВ. Обозначим элементарные объемы, заштрихованные на чертеже, соответственно через 6V^ и SV2.
(ЛТД)] тела АВ. Обозначим элементарные объемы, заштрихованные на чертеже, соответственно через 6V^ и SV2. (3-114)
(3-114) и КД
и КД  Масса жидкости в объеме
Масса жидкости в объеме  есть та масса жидкости, которая за время dt проходит через сечение 1—1:
есть та масса жидкости, которая за время dt проходит через сечение 1—1: . (3-115)
. (3-115) выразилось бы в виде:
выразилось бы в виде: (3-116)
(3-116) (3-117)
(3-117) аналогично (3-117) можем написать:
аналогично (3-117) можем написать: (3-118)
(3-118)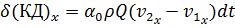 (3-119)
(3-119) время.
время. , (3-123)
, (3-123) (3-124)
(3-124) — масса жидкости, проходящая в единицу времени (в секунду) через любое живое сечение потока,
— масса жидкости, проходящая в единицу времени (в секунду) через любое живое сечение потока,  — количество движения указанной массы в данном плоском живом сечении, к которым относится скорость v; величина
— количество движения указанной массы в данном плоском живом сечении, к которым относится скорость v; величина  может быть названа секундным количеством движения потока (эта величина представляет собой как- бы расход количества движения). Размерность секундного количества движения потока — размерность силы.
может быть названа секундным количеством движения потока (эта величина представляет собой как- бы расход количества движения). Размерность секундного количества движения потока — размерность силы.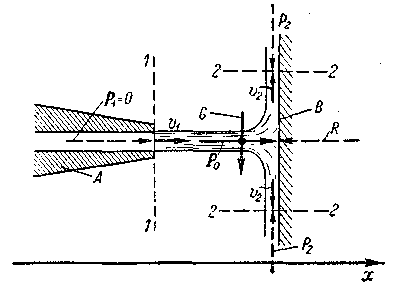
 ) и (
) и (  ) должны давать замкнутый многоугольник сил при условии, если вектор секундного количества движения (
) должны давать замкнутый многоугольник сил при условии, если вектор секундного количества движения ( 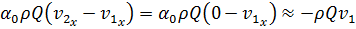
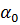 = 1,0).
= 1,0). (так как в сечении 1—1 давление атмосферное); Р2х = 0; Рх — Р1х + P2x = 0; (Т0)х
(так как в сечении 1—1 давление атмосферное); Р2х = 0; Рх — Р1х + P2x = 0; (Т0)х  0; Rx = R = -Р0.
0; Rx = R = -Р0. (
( 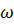 v1)v1
v1)v1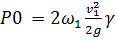 где a>j — площадь живого сечения струи (в сечении 1—1).
где a>j — площадь живого сечения струи (в сечении 1—1).