
|
|
Основные аналитические методы исследования движения жидкостиОСНОВЫ ГИДРОДИНАМИКИ Предварительные указания При рассмотрении движения жидкости, вообще говоря, приходится сталкиваться с двумя различными задачами: 1) с так называемой внешней задачей; здесь задан поток жидкости, требуется же найти силы, приложенные к тому или другому твердому телу, обтекаемому жидкостью; 2) с так называемой внутренней задачей; здесь, наоборот, заданы силы, действующие на жидкость (в частности, объемные силы, например, силы тяжести); требуется же найти так называемые гидродинамические характеристики потока. К числу гидродинамических характеристик потока относятся: а) скорость а движения жидких частиц; б) уже известная из предыдущего (см. гл.2) величина р, которая называется здесь гидродинамическим явлением.[1] В случае идеальной жидкости гидродинамическое давление имеет тот же смысл и обладает теми же свойствами, что и гидростатическое давление р. В случае же реальной (вязкой) жидкости гидродинамическому давлению р приходится придавать особое значение. Дело в том, что при рассмотрении элементарной призмы на рис. 2-4 в случае движения вязкой жидкости приходится учитывать касательные напряжения, возникающие по граням этой призмы (так же как и в случае твердого тела). При этом оказывается, что где Имея в виду такое положение, при анализе движения вязкой жидкости пользуются гипотезой, согласно которой
причем вычисленное таким образом значение р принимают в качестве характеристики давления напряжения) в рассматриваемой точке. Эту величину р и называют гидродинамическим давлением в точке. Как видно, в случае движения вязкой жидкости величина р не является реальным напряжением, а представляет собой среднеарифметическое значение из действительных нормальных напряжений, определенных для трех взаимно перпендикулярных площадок действия, произвольно намеченных в данной точке (считается, что величина р не изменяется с изменением ориентировки этих трех взаимно ортогональных площадок). Ниже, главным образом, будем иметь в виду вторую (внутреннюю) задачу. При этом, как отмечено, решая ее, будем отыскивать величины и и p (зная силы, действующие на жидкость). В отношении мир надо сказать, что в общем случае они для разных точек пространства, занятого жидкостью, имеют различную величину. Кроме того, они для данной точки пространства могут изменяться и во времени. Учитывая сказанное, можем написать:
где Если бы мы нашли функции 1) уравнение несжимаемости и неразрывности движущейся жидкости (иногда это уравнение называют уравнением баланса расхода жидкости); 2) уравнение баланса удельной энергии потока (уравнение Бернулли); 3) гидравлическое уравнение количества движения. Эти три уравнения и составляют основную теоретическую базу технической гидродинамики. В дальнейшем в этой главе мы дадим соответствующий вывод этих уравнений (для случая так называемого установившегося движения жидкости) и подробно их разъясним. Предварительно же остановимся на пояснении некоторых, исходных представлений в основном из области кинематики жидкости. Основные аналитические методы исследования движения жидкости Различают два принципиально разных аналитических метода исследования движения жидкости: метод Лагранжа и метод Эйлера. 1°. Метод Лагранжа. Представим себе некоторую область, занятую движущейся жидкостью (рис. 3-1). Наметим неподвижные оси координат Ох и Oz. Будем рассматривать ряд движущихся частиц жидкости: Мг, /И2, М3, . . ., находящихся в начальный момент времени на границе изучаемой области. Обозначим через х0 и z0 начальные координаты этих жидких частиц. Будем считать, что для каждой частицы М нам известны зависимости
Тогда, пользуясь этими зависимостями, легко можно построить траектории намеченных частиц жидкости. Далее можем в любом месте этих траекторий найти длину пути ds, проходимого частицей за время dt. Деля же ds на dt, можем найти скорость в данной точке; можно так же найти и ускорение любой частицы М в любой точке пространства в тот или другой момент времени. Как видно, в данном случае мы следим за отдельными частицами жидкости в течение времени t, за которое эти частицы, двигаясь по своим траекториям, проходят всю рассматриваемую область. Согласно Лагранжу, о потоке жидкости в целом мы судим по совокупному рассмотрению траекторий, описываемых жидкими частицами. Существенно подчеркнуть, что здесь (в отличие от метода Эйлера; см. ниже) х и zпредставляют собой текущие координаты жидких частиц. Поэтому величины dx и dz должны в данном случае рассматриваться как проекции пути ds на соответствующие координаты. В силу этого, согласно Лагранжу, можем написать:
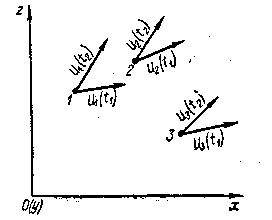
2°. Метод Эйлера. Представим себе снова некоторую область, занятую движущейся жидкостью (рис. 3-2). Согласно Эйлеру, мы не следим за движением отдельных частиц жидкости М и не интересуемся их траекториями.
Рис. 3-1. К методу Лагранжа
Рис. 3-2. К методу Эйлера В соответствии с предложением Эйлера мы намечаем точки 1, 2, 3, . . ., которые считаем скрепленными с рассматриваемым пространством. Эти точки неподвижны при протекании через них жидкости. Здесь величины х и zне есть текущие координаты частиц жидкости, а просто координаты неподвижных точек пространства. Рассмотрим момент времени t1. В этот момент времени в точке 1 (рис. 3-2) будет находиться некоторая частица жидкости, имеющая скорость и t (t1); в этот же момент времени в точке 2 будем иметь скорость и2 ( Как видно, для момента времени t1 поток оказывается представленным векторным полем скоростей, причем каждый вектор скорости относится к определенной неподвижной точке пространства (и к данному моменту времени t). В следующий момент времени в точках 1, 2, 3, ... получаем соответственно скорости и1 (t2), u2 (t2), и3 (t2),и т. д., причем в общем случае получаем другое поле скоростей. Как видно, согласно Эйлеру, поток в целом в данный момент времени оказывается представленным векторным полем скоростей, относящихся к неподвижным точкам пространства. Сопоставляя векторное поле скоростей, отвечающее моменту времени tlt с векторным полем скоростей, отвечающим моменту времени t2t легко можно себе представить, как рассматриваемый поток изменяется с течением времени. Выше было отмечено, что координаты х и z, согласно Эйлеру, являются координатами неподвижных произвольных точек пространства. Поэтому в данном случае величины dx и dz нельзя рассматривать как проекции элементарного пути ds, проходимого частицами жидкости за время dt. Величины dx и dz здесь являются просто произвольными приращениями координат х и z. В связи с этим зависимости (3-4) в случае метода Эйлера — неприемлемы. 3°. Метод исследования движения жидкости, применяемый в гидравлике.Метод Лагранжа ввиду его сложности не нашел широкого применения втехнической механике жидкости. Далее в основном будем пользоваться методом Эйлера. Однако, применяя его, все же не будем совершенно отрешаться от рассмотрения движения частиц жидкости М. Мы будем следить за их движением, но не в продолжение времени t (как это следует по Лагранжу), а в продолжение только элементарного отрезка времени dt, в течение которого данная частица жидкости проходит через рассматриваемую точку пространства. Принимая такую постановку вопроса, можем считать, что в каждой точке пространства за время dt соответствующая частица жидкости проходит путь ds, проекции которого равны dx и dz. При этом, очевидно, для определения проекций скорости их ииг можно будет пользоваться соотношениями (3-4). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 - действительные нормальные напряжения в рассматриваемой точке, относящиеся к трем произвольно намеченным в этой точке взаимно ортогональным площадкам действия.
- действительные нормальные напряжения в рассматриваемой точке, относящиеся к трем произвольно намеченным в этой точке взаимно ортогональным площадкам действия.
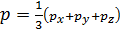
 (3-1)
(3-1) (3-2)
(3-2)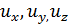 проекции скорости и на оси декартовой (прямоугольной) системы координат.
проекции скорости и на оси декартовой (прямоугольной) системы координат.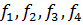 то тем самым и решили бы нашу задачу. Действительно, зная эти функции, мы могли бы для каждой точки пространства найти и и р и установить, чему для данной точки пространства равны величины и и р в различные моменты времени. Однако указанные функции очень часто отыскать нет возможности. Поэтому в гидравлике, как правило, отказываются от использования зависимостей (3-1) и (3-2) и идут по иному пути. В основу решений, приводимых в гидравлике (в технической механике жидкости), полагают другие уравнения, которые все же имеют достаточно общий характер. К числу таких основных уравнений гидравлики относятся следующие три уравнения:
то тем самым и решили бы нашу задачу. Действительно, зная эти функции, мы могли бы для каждой точки пространства найти и и р и установить, чему для данной точки пространства равны величины и и р в различные моменты времени. Однако указанные функции очень часто отыскать нет возможности. Поэтому в гидравлике, как правило, отказываются от использования зависимостей (3-1) и (3-2) и идут по иному пути. В основу решений, приводимых в гидравлике (в технической механике жидкости), полагают другие уравнения, которые все же имеют достаточно общий характер. К числу таких основных уравнений гидравлики относятся следующие три уравнения: (3-3)
(3-3)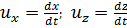 (3-4)
(3-4)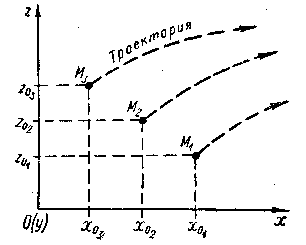
 ) точке 3 — скорость и3(
) точке 3 — скорость и3(  ) и т. д.
) и т. д.