
|
|
НАПРЯЖЕННОЕ СОСТОЯНИЕ ЖИДКОСТИОднородная жидкость, которую мы далее, как правило, и рассматриваем, представляет собой не сплошное (не непрерывное) тело, а тело, состоящее из молекул, расположенных на некотором (весьма небольшом) расстоянии друг от друга. Как видно, жидкость имеет, строго говоря, прерывную (дискретную) структуру. Однако при решении различных гидромеханических задач пренебрегают отмеченным обстоятельством и рассматривают жидкость как сплошную (непрерывную) среду — континуум (от лат. continuum — непрерывное, сплошное). Как видно, при рассмотрении жидкости поступают так же, как и при рассмотрении твердых тел (в строительной механике) или при рассмотрении сыпучих тел (песка — в механике грунта). Модель сплошной среды имеет свою теорию, одинаково применимую (разумеется до определенного предела) и к твердым, и к сыпучим телам, и к жидкости. Выше мы видели, что только в редких случаях жидкость получает существенные разрывы (см. § 1-5). Однако часто и такие разрывы мы исключаем из рассмотрения, причем и здесь пользуемся моделью сплошной среды. Существенно подчеркнуть, что заменив для расчета жидкость сплошной средой, мы приписываем этой сплошной среде те механические свойства, которые были найдены экспериментальным путем для действительной жидкости (в данном случае — для воды); при этом, оперируя сплошной средой, обладающей указанными физическими (механическими) свойствами, мы такое воображаемое тело всюду далее условно называем жидкостью (водой).2 Что касается сил, действующих на воду (рассматриваемую в виде описанной сплошной среды), то их необходимо разделить на две различные группы: внутренние силы, именуемые иногда усилиями, и внешние силы. Внутренними силами называются силы взаимодействия между материальными точками (частицами) жидкости (рассматривая жидкость, как сплошную среду, мы, разумеется, имеем право говорить о «частицах» жидкости, т. е. об элементарных объемах жидкости). Внешние силы — суть силы, приложенные к частицам рассматриваемого объема жидкости со стороны других вещественных тел (или физических полей), в частности, со стороны жидкости, окружающей рассматриваемый ее объем. Внешние силы, действующие на данный объем жидкости, в свою очередь, могут быть разделены также на две группы: 1) Силы массовые. Эти силы действуют на все частицы, составляющие рассматриваемый объем жидкости: величина этих сил пропорциональна массе жидкости. В случае однородной жидкости, т. е. жидкости, имеющей всюду одинаковую плотность
где 2) Силы поверхностные. Эти силы приложены к поверхности, ограничивающей рассматриваемый объем жидкости, выделенный, например, внутри покоящейся или движущейся жидкости (см. объем ABCD жидкости на рис. 1-9). При равномерном распределении этих сил по данной поверхности величина их пропорциональна площади этой поверхности. К числу таких сил относятся, например, атмосферное давление, действующее на так называемую свободную поверхность жидкости, а также силы трения, о которых говорили в § 1-3 (действующие по поверхности, намеченной внутри жидкости). Изучая механическое действие жидкости на поверхность - какого-либо твердого тела, можно говорить о реакции этой поверхности, т. е. реактивной силе, приложенной к жидкости со стороны твердого тела. Такая сила также должна рассматриваться как внешняя поверхностная сила (по отношению к объему жидкости, ограниченному поверхностью упомянутого твердого тела). В общем случае плотность распределения поверхностной силы (т. е. напряжение) в различных точках рассматриваемой поверхности может быть различной. В частном случае, когда поверхностная сила
где Само собой разумеется, что при изучении сил, действующих на жидкое тело, так называемые сосредоточенные силы должны исключаться из рассмотрения. Что касается напряженного состояния жидкости, рассматриваемой как сплошная среда, то этот вопрос легко себе представить на основе тех сведений, которые сообщались, например, в курсе сопротивления материалов применительно к твердому телу. Имеем объем
Рис. 1-9. Объем ABCD, выделенный внутри жидкости (движущейся со скоростью
Рис. 1-10. Напряжение в заданной точке М сплошной среды: (I-I) и (II-II) - главные оси деформации; (
Напряжение в точке М, принадлежащей площадке а) нормальное (к площадке действия) напряжение через б) касательное (к площадке действия) напряжение через Известно, что для данной точки М сплошной напряженной среды можно построить, рассматривая плоскую задачу, так называемый эллипс напряжений (эллипс Ляме), при помощи которого поясняется, как в зависимости от ориентировки площадки действия Рассматривая для точки М некоторую произвольно ориентированную площадку действия вектор нормаль отрезок Следует запомнить, что эллипс напряжений очерчивается по концу вектора а, а не по концу вектора При рассмотрении пространственной задачи вместо эллипса напряжений получаем в общем случае трехосный эллипсоид напряжений, причем в этом случае будем иметь уже не два главных напряжения ( Известно, что в частном случае, когда в рассматриваемом напряженном теле отсутствуют касательные напряжения (такой случай может иметь место, например, когда данное твердое тело является невесомым, причем оно подвергнуто всестороннему равномерному сжатию) эллипсоид напряжений обращается в шаровую поверхность (рис. 1-10, б). Следовательно, при отсутствии касательных напряжений (в рассматриваемом теле) значение (модуль) полного напряжения в любой точке данного тела не зависит от ориентировки площадки действия.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 = const), величина массовых сил будет пропорциональна также объему жидкости; поэтому при
= const), величина массовых сил будет пропорциональна также объему жидкости; поэтому при 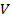 жидкости, равна
жидкости, равна (1-10)
(1-10) — масса объема
— масса объема  и
и 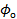 — интенсивность (плотность распределения) рассматриваемой внешней силы, причем
— интенсивность (плотность распределения) рассматриваемой внешней силы, причем 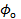 является удельной объемной силой, отнесенной к единице объема жидкости и
является удельной объемной силой, отнесенной к единице объема жидкости и  — удельной объемной силой, отнесенной к единице массы жидкости (по существу величина
— удельной объемной силой, отнесенной к единице массы жидкости (по существу величина  распределяется равномерно по рассматриваемой поверхности площадью S, величина этой силы
распределяется равномерно по рассматриваемой поверхности площадью S, величина этой силы (1-11)
(1-11) — напряжение, вызываемое рассматриваемой внешней поверхностной силой. Из дальнейшего будет видно, что напряжения
— напряжение, вызываемое рассматриваемой внешней поверхностной силой. Из дальнейшего будет видно, что напряжения  ) оказываются не ортогональными к площадкам
) оказываются не ортогональными к площадкам  , на которые они действуют (см. рис. 1-9). В этом случае напряжение
, на которые они действуют (см. рис. 1-9). В этом случае напряжение 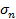 и б) касательную составляющую, которую можно назвать касательным напряжением
и б) касательную составляющую, которую можно назвать касательным напряжением  .
. причем у точки М намечаем элементарную площадку
причем у точки М намечаем элементарную площадку  («площадку действия») определенной ориентировки (т. е. определенного наклона).
(«площадку действия») определенной ориентировки (т. е. определенного наклона).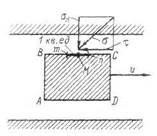
 );
);  - напряжение поверхностной силы, действующей на грань ВС
- напряжение поверхностной силы, действующей на грань ВС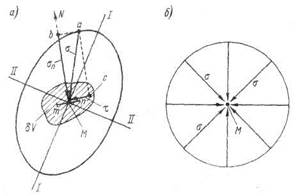
 - эллипс напряжений, б — «шаровая поверхность напряжений» (
- эллипс напряжений, б — «шаровая поверхность напряжений» (  )
) ) - произвольно ориентированная «площадка действия», намеченная в точке М;
) - произвольно ориентированная «площадка действия», намеченная в точке М;  и
и  - нормальное и касательное напряжения в точке М для «площадки действия»
- нормальное и касательное напряжения в точке М для «площадки действия» 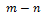
 ;
; .
. и
и 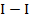 и II —II эллипса будем называть главными осями деформаций элементарного объема
и II —II эллипса будем называть главными осями деформаций элементарного объема 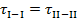 = 0; нормальные напряжения для этих площадок называются главными напряжениями и обозначаются через
= 0; нормальные напряжения для этих площадок называются главными напряжениями и обозначаются через  (большее напряжение) и через
(большее напряжение) и через 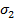 (меньшее напряжение).
(меньшее напряжение).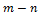 , имеем для нее (рис. 1-10, а):
, имеем для нее (рис. 1-10, а):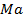 , конец которого (точка
, конец которого (точка  ) лежит на эллипсе; этот вектор дает нам значение (модуль) и направление напряжения
) лежит на эллипсе; этот вектор дает нам значение (модуль) и направление напряжения 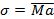
 , вдоль которой действует в данной точке нормальное напряжение
, вдоль которой действует в данной точке нормальное напряжение 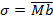
 , ортогональный к нормали
, ортогональный к нормали 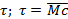
 ), а три главных напряжения (
), а три главных напряжения (  ).
).