
|
|
ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА РЕАЛЬНЫХ ЖИДКОСТЕЙМногие физические свойства жидкостей изучаются в общей физике, а не в гидравлике. Гидравлика, представляя собой особый раздел профессиональной физики, занимается вопросами механики жидкости. Разумеется, при рассмотрении таких вопросов приходится интересоваться численными характеристиками различных свойств разных жидкостей. 1.Плотность жидкости Возьмем некоторый объем Как известно, плотностью жидкости
следовательно,
Введем обозначение:
где
Нам известно, что
где
откуда получаем следующую важную зависимость:
Величины р и у являются числами именованными:
Где Численные значения
Таблица 1-1 Плотность
Для пресной чистой воды
(или 2. Сжимаемость (или объемная упругость) жидкости. Представим себе некоторый объем жидкости Упругой сжимаемостью жидкости называется способность её принимать свой прежний объем V после снятия внешней нагрузки При небольших значениях
причем К называют модулем объемной упругости жидкости. Для воды (в обычных условиях) К = 22 3. Сопротивление жидкости растягивающим усилиям. Особыми физическими опытами было показано, что покоящаяся жидкость (в частности, вода, ртуть) иногда способна сопротивляться очень большим растягивающим усилиям; например, вода в определенных условиях может выдерживать растягивающие напряжения до 2,8 Такого рода сопротивление растягивающим усилиям получается только, когда жидкость находится в особых условиях, не имеющих места в обыденной жизни. В § 1-5 будет отмечено, что жидкость в обычных условиях даже при наличии сжимающих напряжений, приближающихся к нулю, начинает уже обращаться в пар, т. е. перестает существовать. Имея это в виду, в гидравлике считают, что жидкость вовсе не способна сопротивляться растягивающим усилиям.
Рис. 1-2. Условная схема взаимного притяжения тел
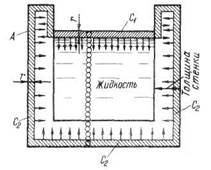
Рис. 1-3. Молекулярное давление C1 — поверхностный слой жидкости, обусловливающий молекулярное давление
4. Сопротивление движущейся жидкости касательным усилиям. Выше было отмечено, что в движущейся реальной жидкости обычно возникают силы трения. Эти силы уравновешивают внутренние касательные усилия, возникающие в жидкости под действием внешних сил. Величина сил трения зависит как от рода жидкости, так и от скорости относительного перемещения частиц жидкости. Этот вопрос подробно разъясняется далее на стр. 134—138; там же попутно приводятся соответствующие численные характеристики так называемой вязкости жидкости, от которой зависит величина сил трения. 5. Молекулярное давление. Жидкость состоит из молекул, которые при определенных условиях с некоторой силой притягиваются друг к другу. Если представить ряд шариков (рис. 1-2), притягивающихся друг к другу с силой F, то ясно, что все они, за исключением крайних (А и В), будут находиться в безразличном состоянии: две силы F, приложенные к каждому внутреннему шарику (со стороны соседних), взаимно уравновешиваются. Что касается крайних шариков А и В, то на каждый из них будет действовать только одна внешняя сила F, причем ясно, что весь «столбик», образованный взаимно притягивающимися шариками (рис. 1-2), должен быть сжат силой F. Имея в виду условную схему на рис. 1-2, можно утверждать, что жидкость, находящаяся в сосуде (рис. 1-3), должна быть сжата своим поверхностным слоем Давление, развиваемое тонким поверхностным слоем Малая сжимаемость жидкости, о чем говорилось ранее, и объясняется тем, что в большинстве случаев внешние силы сравнительно с молекулярным давлением являются незначительными. Важно обратить внимание на следующие обстоятельства.
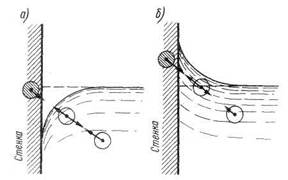
Рис. 1-4. Молекулярное давление поверхностной пленки различной кривизны
а) Считая, что поверхностный слой
Это положение в курсах общей физики доказывается (для «плоской задачи») следующим образом. Рассматриваем молекулу жидкости m, находящуюся вблизи свободной поверхности жидкости Силы притяжения, приложенные к молекуле m со стороны молекул, находящихся в области А (см. чертеж), уравновешиваются силами притяжения молекул, находящихся в области В (симметричной области А). Как видно, можно считать, что рассматриваемая молекула притягивается книзу только теми молекулами, которые находятся в области С, ограниченной сверху горизонтальной линией Так как площадь С, ограниченная сверху линией Рассуждая аналогично, получаем, что Ппл < Пвып. б) Молекулы жидкости, покоящейся в сосуде А (рис. 1-3), следует рассматривать в совокупности с частицами (атомами или ионами) того материала, из которого выполнены стенки сосуда А. При этом легко понять, что система «жидкость — стенки сосуда» будет равномерно сжата поверхностными слоями со всех сторон (см. заштрихованные поверхностные слои: жидкости С1 и материала стенок сосуда С2). Отсюда вытекает следующее: молекулярное давление, как бы оно ни было велико, не может разрушить сосуд, в котором находится жидкость. Это давление внешне не проявляется и не может быть измерено каким-либо простым
Рис. 1-5. Капиллярное поднятие, обусловливаемое разностью молекулярных давлений (
Рис. 1-6. «Несмачиваемая» (а) и «смачиваемая» (б) стенки
Выше в п. 3 было отмечено, что в жидкости иногда могут возникнуть растягивающие усилия. Подчеркнем теперь, что такое растяжение следует понимать только как снижение молекулярного сжимающего давления, обусловленного плоской поверхностной пленкой. 6. Капиллярное поднятие жидкости. Вопросы капиллярности являются весьма существенными в области гидротехники. Покажем на рис. 1-5 сосуд А, наполненный жидкостью, и капиллярную трубку К, один конец которой опущен в жидкость. Выше было показано, что жидкость в сосуде находится под давлением Ппл (развиваемым своим собственным плоским поверхностным слоем). Обратимся теперь к рассмотрению жидкости в капиллярной трубке. Как видно из рис. 1-6, в районе примыкания поверхности жидкости к стенке трубки можем получить одну из следующих картин: если взаимное притяжение двух молекул жидкости велико сравнительно с притяжением молекул жидкости к частице твердой стенки, то получаем схему рис. 1-6, а (случай «несмачиваемой стенки»); если же взаимное притяжение двух молекул жидкости мало сравнительно с притяжением молекул жидкости к частице твердой стенки, то получаем схему на рис. 1-6,6 (случай «смачиваемой стенки»), В том случае, когда диаметр трубки уменьшается, противоположные стенки трубки сближаются, причем схема на рис. 1-6, а приводит нас к выпуклой поверхностной пленке — к выпуклому мениску (рис. 1-7,а); схема же на рис. 1-6,б — к вогнутой поверхностной пленке, т. е. к вогнутому мениску в трубке (рис. 1-7,6). Имея это в виду, можем сказать, что если на поверхность жидкости в сосуде (рис. 1-5) наложен как бы поршень (пресс), развивающий давление Под действием разности давлений Жидкость, находящаяся в трубке (рис. 1-5) и расположенная выше уровня жидкости в сосуде, называется капиллярной, в отличие от остальной жидкости, которая иногда называется здесь гравитационной. Надо подчеркнуть, что никакого различия между капиллярной и гравитационной жидкостями в отношении их физических свойств нет. Законы равновесия и движения жидкости совершенно одинаковы для капиллярной и гравитационной областей. Единственное отличие капиллярной жидкости от гравитационной заключается в том, что первая названная жидкость сжимается несколько меньшим поверхностным молекулярным давлением.
Рис. 1-7. Мениск в случае «несмачиваемой» (а) и «смачиваемой» (б) трубки
Величина Помимо изложенного выше объяснения причин капиллярности, в литературе часто приводится и иная (условная) точка зрения на данный вопрос, в основу которой кладется представление о гипотетической (предположительной, в данном случае несуществующей) силе так называемого поверхностного натяжения. Здесь предполагается, что поясненное выше молекулярное давление обусловливается не взаимным притяжением молекул (см. выше), а натяжением («поверхностным натяжением») некоторой несуществующей (воображаемой) упругой пленки, обтягивающей рассматриваемый объем жидкости; при этом сила растяжения («натяжения») этой пленки принимается такой, чтобы она вызвала реально существующие силы поверхностного молекулярного давления, обусловленные взаимным притяжением молекул (притяжением, которое в этом случае исключается из непосредственного рассмотрения). Как видно, гипотетическое поверхностное натяжение имитируют силы взаимного притяжения молекул, которые в отличие от «поверхностного натяжения» реально существуют. При этом, исходя из этих сил (зная величину молекулярного давления), можно решать (вовсе не используя условное понятие «поверхностного натяжения») все интересующие нас практические задачи на основании обычных правил механики. Важно подчеркнуть, что непосредственно на внутренней поверхности капиллярной трубки (диаметром D), по-видимому, образуется весьма тонкий слой воды (толщиной 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ; вес единицы объема жидкости у.
; вес единицы объема жидкости у.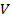 жидкости, имеющий массу
жидкости, имеющий массу  и вес G.
и вес G. (1-1)
(1-1) (1-1')
(1-1') (1-2)
(1-2) — есть вес единицы объема жидкости (ранее эту величину называли «удельным весом» или «объемным весом»); как видно
— есть вес единицы объема жидкости (ранее эту величину называли «удельным весом» или «объемным весом»); как видно (1-2')
(1-2') (1-3)
(1-3) — ускорение свободного падения тела (ускорение силы тяжести). Подставляя в (1-3) выражение (1-
— ускорение свободного падения тела (ускорение силы тяжести). Подставляя в (1-3) выражение (1-  ) и (1-2'), имеем:
) и (1-2'), имеем: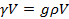 (1-4)
(1-4) (1-5)
(1-5) (1.6)
(1.6) — символы соответственно массы, длины, силы и времени.
— символы соответственно массы, длины, силы и времени.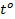 в градусах Цельсия (°С) приводятся в табл. 1-1]. Зависимостью
в градусах Цельсия (°С) приводятся в табл. 1-1]. Зависимостью  и вес, отнесенный к единице объема жидкости («удельный вес»),
и вес, отнесенный к единице объема жидкости («удельный вес»),  , кг/м3
, кг/м3

 внешнего всестороннего давления (напряжения), действующего на него, уменьшается (снижается) на
внешнего всестороннего давления (напряжения), действующего на него, уменьшается (снижается) на 
 р.
р.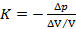
 105 кПа, т. е. К
105 кПа, т. е. К  220 кН/см2 или К
220 кН/см2 или К  22000 кгс/см2.
22000 кгс/см2.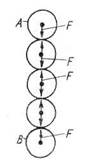
 толщина которого равна радиусу г молекулярного действия. Напомним, что радиус г есть расстояние от центра данной молекулы до точки, где сила притяжения, вызываемая этой молекулой, пренебрежимо мала. Величина г весьма мала.
толщина которого равна радиусу г молекулярного действия. Напомним, что радиус г есть расстояние от центра данной молекулы до точки, где сила притяжения, вызываемая этой молекулой, пренебрежимо мала. Величина г весьма мала.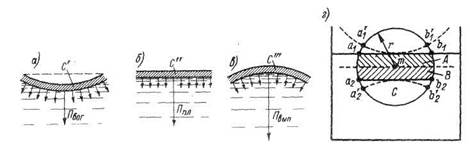
 жидкости (рис. 1-3)2 является совокупностью притягивающихся молекул А (рис. 1-2), можно доказать (основываясь на самых простых соображениях механики), что молекулярное давление Ппл, развиваемое плоской поверхностной пленкой С" (равное для воды 11
жидкости (рис. 1-3)2 является совокупностью притягивающихся молекул А (рис. 1-2), можно доказать (основываясь на самых простых соображениях механики), что молекулярное давление Ппл, развиваемое плоской поверхностной пленкой С" (равное для воды 11  5 кПа, т.е. 11000 кгс/с2 = 11000 атм; рис. 1-4,б), всегда должно быть меньше молекулярного давления ПВЫП) развиваемого выпуклой поверхностной пленкой С" (рис. 1-4, в), и больше молекулярного давления Пвог, развиваемого вогнутой поверхностной пленкой
5 кПа, т.е. 11000 кгс/с2 = 11000 атм; рис. 1-4,б), всегда должно быть меньше молекулярного давления ПВЫП) развиваемого выпуклой поверхностной пленкой С" (рис. 1-4, в), и больше молекулярного давления Пвог, развиваемого вогнутой поверхностной пленкой  (рис. 1-4,а):
(рис. 1-4,а):
 (рис. 1-4,г). Другие молекулы, находящиеся в пределах окружности, описанной радиусом молекулярного действия
(рис. 1-4,г). Другие молекулы, находящиеся в пределах окружности, описанной радиусом молекулярного действия  (см. чертеж), притягивают рассматриваемую молекулу m. Притяжением молекул воздуха пренебрегаем.
(см. чертеж), притягивают рассматриваемую молекулу m. Притяжением молекул воздуха пренебрегаем. (в случае плоской свободной поверхности
(в случае плоской свободной поверхности  (в случае вогнутой свободной поверхности
(в случае вогнутой свободной поверхности  ).
). прибором. В связи с этим, говоря о давлении внутри жидкости или о давлении жидкости на ту или другую стенку, мы далее не будем учитывать молекулярного давления, считая, что оно как бы совсем не существует. Исключение здесь будет составлять только вопрос о капиллярности (см. п. 6).
прибором. В связи с этим, говоря о давлении внутри жидкости или о давлении жидкости на ту или другую стенку, мы далее не будем учитывать молекулярного давления, считая, что оно как бы совсем не существует. Исключение здесь будет составлять только вопрос о капиллярности (см. п. 6).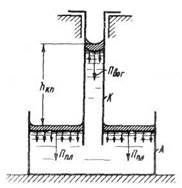
 )
)
 (для воды
(для воды  кПа) то на поверхность жидкости в трубке наложен поршень, развивающий давление или или (рис. 1-5).
кПа) то на поверхность жидкости в трубке наложен поршень, развивающий давление или или (рис. 1-5).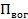 и происходит поднятие жидкости в «смачиваемой» трубке на высоту
и происходит поднятие жидкости в «смачиваемой» трубке на высоту  (рис. 1-5); под действием же разности давлений
(рис. 1-5); под действием же разности давлений  и
и 
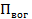 или
или  , измеряемый, возможно, долями миллиметра), механические характеристики которого отличны от механических характеристик обычной воды. Согласно модели, предлагаемой отдельными специалистами, указанный слой может быть назван слоем «твердой воды». Считают, что такая твердая вода, рассматриваемая как сплошная среда, способна, находясь в покое, выдерживать (в отличие от обычной воды) касательные напряжения
, измеряемый, возможно, долями миллиметра), механические характеристики которого отличны от механических характеристик обычной воды. Согласно модели, предлагаемой отдельными специалистами, указанный слой может быть назван слоем «твердой воды». Считают, что такая твердая вода, рассматриваемая как сплошная среда, способна, находясь в покое, выдерживать (в отличие от обычной воды) касательные напряжения  . Отсюда ясно, что в соответствии с отмеченной моделью, когда D
. Отсюда ясно, что в соответствии с отмеченной моделью, когда D  , вода в тонкой трубке при определенных условиях не в состоянии будет двигаться (преодолевая касательные напряжения
, вода в тонкой трубке при определенных условиях не в состоянии будет двигаться (преодолевая касательные напряжения