Указания и подсказки к решению задач
1. Возможно, вы находили среднюю скорость как среднее арифметическое и потому получили одинаковые ответы. Запишите определение средней скорости и обратите внимание, что в первом случае автомобиль двигался половину времени, а во втором – половину пути со скоростью  . .
2. Выберите систему координат, сделайте схематический чертеж и попробуйте записать уравнение движения. Если вам это удастся, из него можно будет найти начальную скорость. Если есть сложности с записью закона движения, см. п. 19.
3. Найдем время, которое необходимо для подъема на высоту  м при начальной скорости м при начальной скорости  м/с. Из уравнения (1.6) м/с. Из уравнения (1.6)
 . (1.6) . (1.6)
найдем  с, с,  с. Таким образом, камень будет на данной высоте дважды: первый раз через 1 с (когда поднимается) и второй – через 6 с (когда опускается). Аналогично и во втором случае найдем с. Таким образом, камень будет на данной высоте дважды: первый раз через 1 с (когда поднимается) и второй – через 6 с (когда опускается). Аналогично и во втором случае найдем  с, с,  с. Окончательный анализ можно проверить в п. 55. с. Окончательный анализ можно проверить в п. 55.
4. Пусть лодка начинает движение из точки О, которую примем за начало координат. Направим ось  вдоль движения реки, тогда ось вдоль движения реки, тогда ось  совпадет с тем направлением, в котором двигалась бы лодка, если бы не было течения, т.е. она попала бы на противоположный берег в точке совпадет с тем направлением, в котором двигалась бы лодка, если бы не было течения, т.е. она попала бы на противоположный берег в точке  . В действительности лодка попадает в некоторую точку, которая находится ниже по течению от точки . В действительности лодка попадает в некоторую точку, которая находится ниже по течению от точки  . Скорость лодки относительно воды совпадает с направлением оси . Скорость лодки относительно воды совпадает с направлением оси  , скорость течения – с направлением оси , скорость течения – с направлением оси  , результирующую скорость , результирующую скорость  можно найти по правилу сложения векторов (п. 47). Сравните свой чертеж с чертежом на рис. к п. 58. Если вы не знаете, как найти результирующую скорость, – см. п. 34. можно найти по правилу сложения векторов (п. 47). Сравните свой чертеж с чертежом на рис. к п. 58. Если вы не знаете, как найти результирующую скорость, – см. п. 34.
17. Время движения камня вверх равняется времени его падения на землю, значение скорости начала движения камня равняется значению скорости его падения.
18. Чему равняется координата  , когда камень упадет на землю? Понятно, как найти время? Если нет – см. п. 36. , когда камень упадет на землю? Понятно, как найти время? Если нет – см. п. 36.
19. Ось  направим вертикально вверх, начало координат выберем в точке, где находилось тело в начальный момент времени. Тогда в уравнении (1.6) направим вертикально вверх, начало координат выберем в точке, где находилось тело в начальный момент времени. Тогда в уравнении (1.6)
 . (1.6) . (1.6)
начальная скорость будет иметь знак «+», а ускорение свободного падения – знак «–».
20. По определению средняя скорость равняется отношению всего пути ко всему времени движения. Путь и время в задаче не заданы, но известно, что первую половину времени (пути во втором случае) автомобиль двигался со скоростью  , а вторую половину времени (пути) – с , а вторую половину времени (пути) – с  . Попробуйте выразить путь или время через скорости. Если все-таки не понятно, что делать дальше, – см. п. 31. . Попробуйте выразить путь или время через скорости. Если все-таки не понятно, что делать дальше, – см. п. 31.
21. По условию задачи надо найти максимальную высоту подъема. Запишите уравнение движения и вспомните, что математически означает максимум или чему равняется Vy в верхней точке траектории (п. 44). Если вы вспомните условие максимума, тогда из него можно будет найти  – время, которое отвечает максимальной высоте подъема – время, которое отвечает максимальной высоте подъема  , а потом и само значение , а потом и само значение  . .
26. Движение лодки относительно берега состоит из движения лодки относительно воды и движения воды относительно берега. Выполните чертеж и примените закон сложения скоростей (п. 43). Если вы не можете сделать чертеж для пунктов а) и б) – см. п. 53, для пункта в) – п. 4. Проверить чертеж можно в пп. 57-58.
29. Найдем скорость камня через 6 с.  м/с. Знак «–» указывает на то, что в этот момент камень будет иметь скорость, направленную не вверх, а вниз. Другими словами, если бросить камень вверх со скоростью м/с. Знак «–» указывает на то, что в этот момент камень будет иметь скорость, направленную не вверх, а вниз. Другими словами, если бросить камень вверх со скоростью  м/с, то он достигнет высоты м/с, то он достигнет высоты  м не за 6 с, а раньше, и в момент м не за 6 с, а раньше, и в момент 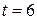 с он будет на этой высоте вторично. Найдите момент времени, когда тело проходит высоту с он будет на этой высоте вторично. Найдите момент времени, когда тело проходит высоту  м в первом и втором случаях. Проверить ваши соображения можно в п. 3. Окончательный анализ результата приведен в п. 55. м в первом и втором случаях. Проверить ваши соображения можно в п. 3. Окончательный анализ результата приведен в п. 55.
30. Из условия максимума высоты следует, что Vy = 0, откуда 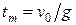 . .
31. Рассмотрим первый случай. Из условия задачи следует, что 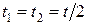 . Автомобиль двигается равномерно прямолинейно, тогда пути можно рассчитать как . Автомобиль двигается равномерно прямолинейно, тогда пути можно рассчитать как 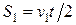 и и  . Остается лишь подставить эти выражения в формулу для расчета средней скорости. Аналогично действуйте и во втором случае. Если не получилось, – см. п. 45. . Остается лишь подставить эти выражения в формулу для расчета средней скорости. Аналогично действуйте и во втором случае. Если не получилось, – см. п. 45.
33. а) 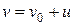 ; б) ; б)  . .
34.  . .
35. Средняя скорость движения в общем случае не равняется средней арифметической от скоростей на разных участках пути.
36. Когда тело упадет на землю, его координата  . Уравнение . Уравнение  имеет два решения имеет два решения  и и  , второй ответ соответствует началу движения. , второй ответ соответствует началу движения.
43. Если известна скорость тела  в системе отсчета, которая двигается относительно некоторой условно неподвижной системы отсчета со скоростью в системе отсчета, которая двигается относительно некоторой условно неподвижной системы отсчета со скоростью  , то при переходе к неподвижной системе отсчета результирующая скорость тела в этой системе отсчета , то при переходе к неподвижной системе отсчета результирующая скорость тела в этой системе отсчета  определяется: определяется: 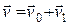 . .
44. Математически условие экстремума означает, что касательная к графику горизонтальна или Vy = 0, а функция изменяет свой знак при переходе через точку экстремума.
45. Из условия задачи следует, что 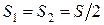 . Автомобиль двигается равномерно прямолинейно, тогда время можно рассчитать как . Автомобиль двигается равномерно прямолинейно, тогда время можно рассчитать как  и и  . .
46. Для анализа полученного результата сделаем дополнительные расчеты. Найдите скорость камня через 6 с после начала движения. Теперь можете объяснить результат? Если нет – см. п. 29.
 47. В этом случае удобно воспользоваться правилом треугольника или, как называют его в иностранной литературе, методом «хвост к голове». Ведь для того, чтобы сложить векторы 47. В этом случае удобно воспользоваться правилом треугольника или, как называют его в иностранной литературе, методом «хвост к голове». Ведь для того, чтобы сложить векторы  и и  (рис. к п. 47 а), надо переместить вектор (рис. к п. 47 а), надо переместить вектор  параллельно самому себе так, чтобы его начало совпадало с концом вектора параллельно самому себе так, чтобы его начало совпадало с концом вектора  (рис. к п. 47 б), тогда их суммой будет вектор (рис. к п. 47 б), тогда их суммой будет вектор  , начало которого совпадает с началом вектора , начало которого совпадает с началом вектора  , а конец – с концом вектора , а конец – с концом вектора  (рис. к п. 47 в). Результат не изменится, если поменять векторы (рис. к п. 47 в). Результат не изменится, если поменять векторы  и и  местами. местами.
53. Пусть лодка начинает движение из точки О, которую примем за начало координат. Направим ось  вдоль движения лодки. В случае а) направление течения совпадает с направлением движения лодки, а в случае б) направлено в противоположную сторону. Примените правило сложения скоростей (п. 43), проверить уравнение в проекции на ось вдоль движения лодки. В случае а) направление течения совпадает с направлением движения лодки, а в случае б) направлено в противоположную сторону. Примените правило сложения скоростей (п. 43), проверить уравнение в проекции на ось  можно в п. 33. можно в п. 33.
54. Надо применить уравнения (1.6).
 . (1.6) . (1.6)
Время вы нашли раньше.
55. Таким образом, оба рассмотренных случая относятся не к подъему, а к спуску. Но для того, чтобы достичь таким путем высоты  за 3 с нужна, очевидно, меньшая начальная скорость, чем для того, чтобы сделать это за 6 с. Из анализа также следует, что достичь высоты за 3 с нужна, очевидно, меньшая начальная скорость, чем для того, чтобы сделать это за 6 с. Из анализа также следует, что достичь высоты  м за 6 с или за 3 с можно лишь при спуске. При подъеме это невозможно сделать при любой начальной скорости. м за 6 с или за 3 с можно лишь при спуске. При подъеме это невозможно сделать при любой начальной скорости.
 56. Перечитайте внимательно п. 21 и п. 44, если все-таки не ясно – п. 30. 56. Перечитайте внимательно п. 21 и п. 44, если все-таки не ясно – п. 30.
57. Рис. к п. 57.
58. Рис. к п. 58.
70. Возможно, вы не применили закон сложения скоростей. Проверьте ваше решение в п. 4.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
. м при начальной скорости
м при начальной скорости  м/с. Из уравнения (1.6)
м/с. Из уравнения (1.6) . (1.6)
. (1.6) с,
с,  с. Таким образом, камень будет на данной высоте дважды: первый раз через 1 с (когда поднимается) и второй – через 6 с (когда опускается). Аналогично и во втором случае найдем
с. Таким образом, камень будет на данной высоте дважды: первый раз через 1 с (когда поднимается) и второй – через 6 с (когда опускается). Аналогично и во втором случае найдем  с,
с,  с. Окончательный анализ можно проверить в п. 55.
с. Окончательный анализ можно проверить в п. 55. вдоль движения реки, тогда ось
вдоль движения реки, тогда ось  совпадет с тем направлением, в котором двигалась бы лодка, если бы не было течения, т.е. она попала бы на противоположный берег в точке
совпадет с тем направлением, в котором двигалась бы лодка, если бы не было течения, т.е. она попала бы на противоположный берег в точке  . В действительности лодка попадает в некоторую точку, которая находится ниже по течению от точки
. В действительности лодка попадает в некоторую точку, которая находится ниже по течению от точки  можно найти по правилу сложения векторов (п. 47). Сравните свой чертеж с чертежом на рис. к п. 58. Если вы не знаете, как найти результирующую скорость, – см. п. 34.
можно найти по правилу сложения векторов (п. 47). Сравните свой чертеж с чертежом на рис. к п. 58. Если вы не знаете, как найти результирующую скорость, – см. п. 34. . Попробуйте выразить путь или время через скорости. Если все-таки не понятно, что делать дальше, – см. п. 31.
. Попробуйте выразить путь или время через скорости. Если все-таки не понятно, что делать дальше, – см. п. 31. – время, которое отвечает максимальной высоте подъема
– время, которое отвечает максимальной высоте подъема  , а потом и само значение
, а потом и само значение  м/с. Знак «–» указывает на то, что в этот момент камень будет иметь скорость, направленную не вверх, а вниз. Другими словами, если бросить камень вверх со скоростью
м/с. Знак «–» указывает на то, что в этот момент камень будет иметь скорость, направленную не вверх, а вниз. Другими словами, если бросить камень вверх со скоростью 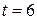 с он будет на этой высоте вторично. Найдите момент времени, когда тело проходит высоту
с он будет на этой высоте вторично. Найдите момент времени, когда тело проходит высоту 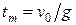 .
.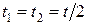 . Автомобиль двигается равномерно прямолинейно, тогда пути можно рассчитать как
. Автомобиль двигается равномерно прямолинейно, тогда пути можно рассчитать как 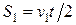 и
и  . Остается лишь подставить эти выражения в формулу для расчета средней скорости. Аналогично действуйте и во втором случае. Если не получилось, – см. п. 45.
. Остается лишь подставить эти выражения в формулу для расчета средней скорости. Аналогично действуйте и во втором случае. Если не получилось, – см. п. 45.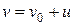 ; б)
; б)  .
. .
. . Уравнение
. Уравнение  имеет два решения
имеет два решения  и
и  , второй ответ соответствует началу движения.
, второй ответ соответствует началу движения. в системе отсчета, которая двигается относительно некоторой условно неподвижной системы отсчета со скоростью
в системе отсчета, которая двигается относительно некоторой условно неподвижной системы отсчета со скоростью  , то при переходе к неподвижной системе отсчета результирующая скорость тела в этой системе отсчета
, то при переходе к неподвижной системе отсчета результирующая скорость тела в этой системе отсчета 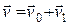 .
.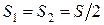 . Автомобиль двигается равномерно прямолинейно, тогда время можно рассчитать как
. Автомобиль двигается равномерно прямолинейно, тогда время можно рассчитать как  и
и  .
. 47. В этом случае удобно воспользоваться правилом треугольника или, как называют его в иностранной литературе, методом «хвост к голове». Ведь для того, чтобы сложить векторы
47. В этом случае удобно воспользоваться правилом треугольника или, как называют его в иностранной литературе, методом «хвост к голове». Ведь для того, чтобы сложить векторы  и
и  (рис. к п. 47 а), надо переместить вектор
(рис. к п. 47 а), надо переместить вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  56. Перечитайте внимательно п. 21 и п. 44, если все-таки не ясно – п. 30.
56. Перечитайте внимательно п. 21 и п. 44, если все-таки не ясно – п. 30.