
|
|
Задачи для работы в аудитории12 Практическое занятие 1 КИНЕМАТИКА. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Примеры решения задач
Задача 1.1. Велосипедист ехал из одного города в другой. Половину пути он ехал со скоростью
Среднюю скорость найдем как
Будем иметь в виду, что по условию задачи
то есть
а
Тогда средняя скорость на всем пути
Задача 1.2. Два поезда идут навстречу друг другу со скоростями Решение. Выберем систему координат, связанную с первым поездом. Тогда относительно этой системы отсчета второй поезд движется со скоростью
Задача 1.4. Тело бросили вертикально вверх с начальной скоростью Решение. Ось
а для второго
По условию задачи
где
Решив систему относительно
1.14. Первую половину времени своего движения автомобиль двигался со скоростью – Средняя скорость в обоих случаях у меня одинаковая – п. 1. – Не знаю, с чего начинать – п. 20. – Не понимаю, как получить рабочую формулу для второго случая – п. 45. – Не могу проанализировать ответ – п. 35. 1.15.Найти скорость – Не знаю, с чего начинать – п. 26. – Алгоритм решения понятен, но ответ не совпадает – п. 70. 1.16. Камень бросили вертикально вверх с поверхности земли со скоростью – Не знаю, с чего начинать – п. 2. – Нет плана решения – п. 21. – Не могу найти время подъема – Не могу найти время – Не знаю, как найти скорость – Не могу проанализировать решение – п. 17. 1.17. Камень бросили вертикально вверх. Какая должна быть начальная скорость, чтобы его подъем на высоту – Не знаю, с чего начинать – п. 2. – Не могу записать уравнения движения – п. 19. – Из решения следует, что для более быстрого подъема на одну и ту же высоту нужна меньшая скорость. Не могу объяснить такой результат – п. 46.
Задачи для работы в аудитории
1.23. Человек последовательно прошел на север 3 км, на восток – 4 км, на север – 1 км и на запад – 1 км. Чему равен пройденный путь и модуль перемещения? 1.24. Самолет пролетел по прямой 150 км, а потом повернул на 90° и пролетел еще 200 км. Найдите пройденный самолетом путь и модуль перемещения. 1.27. Самолет, взлетевший с аэродрома на антарктической научной станции, взял курс на восток. Пролетев 300 км, он повернул на юг и, пролетев еще 300 км, достиг Южного полюса. На каком расстоянии от Южного полюса находится аэродром? Нарисуйте примерный вид траектории движения. 1.30. Велосипедист проехал 3/4 расстояния от поселка А до поселка В за один час. С какой скоростью он двигался, если, увеличив скорость до 25 км/ч, он за следующий час добрался до поселка В и вернулся в поселок А? 1.36. Пешеход две трети времени своего движения шел со скоростью 3 км/ч, а оставшееся время – со скоростью 6 км/ч. Какова была его средняя скорость на всем пути? 1.37. Точка прошла половину пути со скоростью v0. На оставшейся части пути она половину времени двигалась со скоростью v1, а последний участок прошла со скоростью v2. Найти среднюю за все время движения скорость точки. 1.43. Катер, двигаясь вниз по реке, обогнал плот в пункте А. Через τ = 60 мин. после этого он повернул обратно и затем встретил плот на расстоянии l = 6,0 км ниже пункта А. Найти скорость течения, если при движении в обоих направлениях мотор катера работал одинаково. 1.51. Корабль движется по экватору на восток со скоростью v0 = 30 км/ч. С юго-востока под углом φ = 60° к экватору дует ветер со скоростью u = 15 км/ч. Найти скорость v' ветра относительно корабля и угол φ' между экватором и направлением ветра в системе отсчета, связанной с кораблем. 1.65. Расстояние между двумя станциями s = 3 км поезд метро проходит со средней скоростью vср = 54 км/ч. При этом на разгон он затрачивает время t1 = 20 с, затем идет равномерно некоторое время t2 и на замедление до полной остановки тратит время t3 = 10 c. Построить график скорости движения поезда и определить наибольшую скорость vмакс поезда.
Задачи для самостоятельного решения
1.33. Первую половину времени своего движения автомобиль движется со скоростью 80 км/ч, а вторую половину времени – со скоростью 40 км/ч. Какова средняя скорость движения автомобиля? 1.34. Первую половину своего пути автомобиль двигался со скоростью 80 км/ч, а вторую половину пути – со скоростью 40 км/ч. Какова средняя скорость движения автомобиля? 1.45. Колонна войск длиной 400 м движется со скоростью 4 км/ч. Командир на коне ездит вдоль колонны со скоростью 20 км/ч. Сколько времени уходит у него на то, чтобы проехать от одного конца колонны до другого и обратно? 1.54. Поезд начал тормозить при скорости 72 км/ч. Какова его скорость после прохождения двух третей тормозного пути?
1.58. График зависимости ускорения тела от времени имеет форму, изображенную на рисунке. Начертить графики зависимости скорости и пути, пройденного телом, от времени. Начальная скорость тела равна нулю (на участке разрыва ускорение равно нулю). 1.64. Пройдя 3/8 длины моста, собака услышала сигнал догоняющего её автомобиля. Если собака побежит назад, то встретится с автомобилем у одного конца моста, а если побежит вперед, то встретится с ним у другого конца моста. Во сколько раз скорость автомобиля больше скорости собаки? 1.66. Поезд метро прошел отрезок между двумя станциями за t = 3 мин. со средней скоростью vср = 55 км/ч. При этом на разгон в начале движения и торможение перед остановкой ушло в общей сложности t1 = 0,5 мин., а остальное время поезд двигался с постоянной скоростью. Чему равна эта скорость u?
ОТВЕТЫ 1.14. 1.15.а) г) 1.16. 1.17. 1.18. 1.19. 1.20. 1.21.Время полета не изменится, дальность увеличится в два раза. 1.22. 1.23.9 км; 5 км. 1.24.350 км; 250 км. 1.25. 1.26.а) 1,57 км; 1,41 км; б) 3,14 км; 2 км; в) 6,28 км; 0; г) 9,42 км; 2 км. 1.27.См. рисунок. Аэродром находится на расстоянии 300 км от Южного полюса. 1.28.9 км/ч. 1.29.Через 2 ч. 1.30.15 км/ч. 1.31.2 км/ч; 4 км/ч. 1.32.55 км/ч. 1.33.60 км/ч. 1.34.53,3 км/ч. 1.35.Первый. 1.36.4 км/ч. 1.37. 1.38.1 мин; 15 с. 1.39. 1.40.За 2 ч. 40 мин. 1.41.6 ч. 1.42.Увеличилась в 3 раза. 1.43.3 км/ч. 1.44.4 км/ч; 16 км/ч. 1.45.2,5 мин. 1.46.1,5 мин. 1.47. 1.48.600 м/с. 1.49.а) на 120 м; 40 с; б) вверх по реке под углом 53º к берегу; 50 с. 1.50.Увеличилась в 1.51.40 км/ч; 19º. 1.52.174 км/ч; на северо-запад под углом 4º27' к меридиану. 1.53.10 м/с2; 300 м/с. 1.54. 1.55.Да; 30 с:, 325 м. 1.56. 1.57.См. график. 1.58.См. график. 1.59. 1.60.15 с. 1.61.114 км/ч. 1.62.За 2 с; за 40 с. 1.63.Нет. 1.64.В 4 раза. 1.65.16,2 м/c; см. график. 1.66.60 км/ч. 1.67.17 м/с. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 км/ч. Далее половину оставшегося времени он прошел со скоростью
км/ч. Далее половину оставшегося времени он прошел со скоростью  км/ч, а потом снова ехал со скоростью
км/ч, а потом снова ехал со скоростью 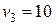 км/ч. Определить среднюю скорость велосипедиста на всем пути.
км/ч. Определить среднюю скорость велосипедиста на всем пути. Решение.На каждом участке велосипедист движется равномерно прямолинейно. Сделаем схематический чертеж (рис. 1.3), на котором обозначим всю траекторию движения. Начало отсчета движения – точка 0, движение разобьем на три отрезка
Решение.На каждом участке велосипедист движется равномерно прямолинейно. Сделаем схематический чертеж (рис. 1.3), на котором обозначим всю траекторию движения. Начало отсчета движения – точка 0, движение разобьем на три отрезка  . На каждом из них обозначим скорости
. На каждом из них обозначим скорости  и время движения
и время движения 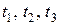 . Запишем уравнение движения для каждого отрезка пути
. Запишем уравнение движения для каждого отрезка пути .
. .
.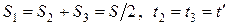 ,
, ,
, .
. км/ч.
км/ч. = 36 км/ч и
= 36 км/ч и  км/ч. Пассажир в первом поезде замечает, что второй поезд проходит мимо него за время
км/ч. Пассажир в первом поезде замечает, что второй поезд проходит мимо него за время  с. Какова длина второго поезда?
с. Какова длина второго поезда?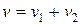 , т.е. относительно пассажира первого поезда второй поезд движется со скоростью
, т.е. относительно пассажира первого поезда второй поезд движется со скоростью  . Таким образом, длина второго поезда равняется:
. Таким образом, длина второго поезда равняется: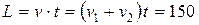 м.
м. . Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определить, на каком расстоянии
. Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определить, на каком расстоянии  от точки броска эти тела встретятся. Сопротивлением воздуха пренебречь.
от точки броска эти тела встретятся. Сопротивлением воздуха пренебречь. направим вверх, начало координат расположим в точке броска. Высоту, на которой тела встретились, обозначим через
направим вверх, начало координат расположим в точке броска. Высоту, на которой тела встретились, обозначим через  , а второе -
, а второе - 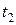 . Запишем уравнение движения для первого тела в виде
. Запишем уравнение движения для первого тела в виде ,
, .
. . Второе тело бросили позже на время, которое равняется времени максимального подъема, т.е.
. Второе тело бросили позже на время, которое равняется времени максимального подъема, т.е. ,
, .
. .
.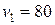 км/ч, а вторую половину времени – со скоростью
км/ч, а вторую половину времени – со скоростью  км/ч. Чему равна средняя скорость
км/ч. Чему равна средняя скорость  движения автомобиля? Как изменится ответ, если первую половину своего пути автомобиль двигался со скоростью
движения автомобиля? Как изменится ответ, если первую половину своего пути автомобиль двигался со скоростью 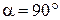 к течению; г) лодки, которая плывет под углом
к течению; г) лодки, которая плывет под углом  м/с, скорость лодки относительно воды
м/с, скорость лодки относительно воды 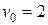 м/с.
м/с. , время
, время 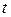 , за которое камень упадет на землю, и скорость
, за которое камень упадет на землю, и скорость  – п. 56.
– п. 56. 29,4 м длился
29,4 м длился 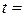 6 с? Как изменится ответ, если сократить время подъема до 3 с? Проанализируйте ответ. Сопротивлением воздуха пренебречь.
6 с? Как изменится ответ, если сократить время подъема до 3 с? Проанализируйте ответ. Сопротивлением воздуха пренебречь. 1.67. По графику vx(t) (см. рис.) найдите среднюю скорость прямолинейного движения (в течение первой и третьей минут движения график представляет собой четверть окружности). Может ли приведенный график точно описывать какое-либо реальное движение?
1.67. По графику vx(t) (см. рис.) найдите среднюю скорость прямолинейного движения (в течение первой и третьей минут движения график представляет собой четверть окружности). Может ли приведенный график точно описывать какое-либо реальное движение? 1.57. График зависимости скорости некоторого тела от времени изображен на рисунке. Начертить графики зависимости ускорения и координаты тела, а также пройденного им пути от времени.
1.57. График зависимости скорости некоторого тела от времени изображен на рисунке. Начертить графики зависимости ускорения и координаты тела, а также пройденного им пути от времени. км/ч,
км/ч, 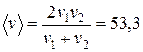 км/ч.
км/ч.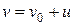 = 3 м/с; б)
= 3 м/с; б)  = 1 м/с; в)
= 1 м/с; в)  м/с;
м/с;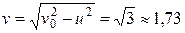 м/с.
м/с.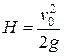 ,
, 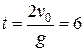 с,
с,  .
. м/с,
м/с,  м/с.
м/с. с,
с,  м,
м,  .
.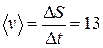 м/с,
м/с, 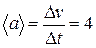 м/с2.
м/с2.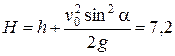 м,
м,  .
. см.
см. 110 м; 50 м.
110 м; 50 м.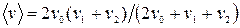 .
.
 За 20 с. (ответ не зависит от скорости поездов)
За 20 с. (ответ не зависит от скорости поездов) 45 с.
45 с. раз.
раз.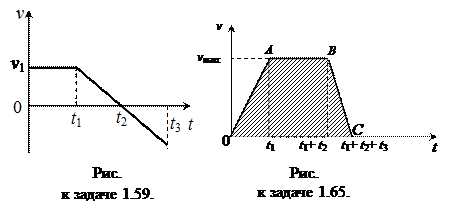 42 км/ч.
42 км/ч. ; см. график.
; см. график.