
|
|
ЛЕКЦИЯ № 5 ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
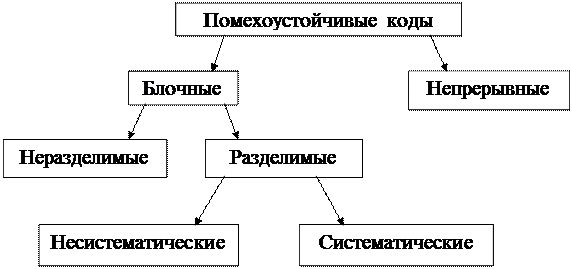
5.1 Классификация помехоустойчивых кодов. Помехоустойчивое (канальное, избыточное, корректирующее) кодирование позволяет обнаруживать и исправлять ошибки, возникающие при передаче сообщения по каналу связи или в ходе других информационных процессов. Помехоустойчивое кодирование за счет введения в состав передаваемых кодовых слов достаточного большого объема избыточной информации, например, в форме проверочных символов. Операцию введения избыточности для повышения помехоустойчивости называют собственно помехоустойчивым кодированием. По способу кодирования помехоустойчивые коды можно разделить на:
Блочное (блоковое) кодирование состоит в том, что каждой букве сообщения или последовательности из k символов, соответствующей этой букве сообщения, ставится в соответствие блок из n символов, причем n > k, а каждый символ блока формируется из k символов исходной последовательности по определенному правилу. На практике блок может достигать от 3 до нескольких сотен единиц. Непрерывные коды характеризуются тем, что кодирование и декодирование информационной последовательности символов осуществляется без разбиения на блоки. Каждый символ выходной последовательности как результат некоторой операции над символами входной последовательности. В таких кодах результат декодирования предыдущих и последующих символов может влиять на декодирование текущего символа. Наиболее широкое распространение среди непрерывных кодов получили сверточные коды. Блочные коды подразделяются на разделимые и неразделимые. К разделимым кодам относятся те, у которых кодовая комбинация состоит из двух частей, а именно информационной и проверочной частей. Обычно проверочные символы получаются посредством некоторых операций над информационными символами. Разделимые коды обозначают (n, k). К неразделимым относятся коды, у которых кодовую комбинацию нельзя разделить на эти две части - информационную и проверочную. Например, код с постоянным весом. Самый большой класс разделимых кодов составляют систематические, у которых значение проверочных символов определяется в результате проведения некоторых операций над информационными символами, поэтому эти коды часто называют линейными. Последовательность линейных операторов и число проверочных символов определяются тем, сколько ошибок может обнаружить и исправить данный код. Проверочные символы могут располагаться в любом месте кодовой комбинации, чаще их располагают справа, т.е. в младших разрядах. Пример формирования блокового разделимого системного кода.
Исходная комбинация k=4
   0 0
Кодовая последовательность n=5
Код (5,4) В примере всего один проверочный символ, который формируется путем сложения по модулю 2 всех информационных символов. Такой код называется кодом с проверкой на четность. Причем, если новую так называемую разрешенную кодовую комбинацию систематического кода можно получить линейным преобразованием двух разрешенных комбинаций, то код называется линейным. К несистематическим кодам относятся те, в которых проверочные символы формируются за счет нелинейных операций над информационными символами (код Бергера).
5.2 Параметры (характеристики) помехоустойчивых кодов и их границы. Корректирующие свойства кодов. Основными характеристиками помехоустойчивых кодов являются: 1. Длина кода n; 2. Основание кода m; 3. Общее число кодовых комбинаций N; 4. Число разрешенных кодовых комбинаций Nр; 5. Избыточность кода 6. Кодовое расстояние d.
Длина кода - число символов в кодовой комбинации n. Если кодовые комбинации содержат одинаковое число символов, то они называются равномерными. Основание кода - это число различных символов кода, т.е это основание системы счисления, которую используют для кодирования.
Если коды двоичные, то Число разрешенных кодовых комбинаций Nр для разделимых определяется из общего числа выходных последовательностей только последовательностями, соответствующими входным.
Главное, что запрещенные кодовые комбинации для передачи информации не используются.
Избыточность кода
Избыточность кода показывает, какая доля кодовых комбинаций не используется для передачи информации, а используется для повышения помехоустойчивости. Для двоичных кодов
Кодовое расстояние d - число позиций, в которых две кодовые комбинации отличаются друг от друга. Кодовое расстояние можно найти в результате сложения по модулю 2 одноименных разрядов кодовой комбинации.
Например. A=01101 B=10111 11010 → d=3
Кодовое расстояние часто называют кодом Хемминга. Кодовое расстояние между различными комбинациями конкретного кода может быть различным. Минимальное кодовое расстояние Декодирование после приема может производиться таким образом, что принятая комбинация отождествляется с той разрешенной, которая находится от нее на наименьшем кодовом расстоянии. Такое декодирование называется декодированием по методу максимального правдоподобия. Например, при d=1 все кодовые комбинации называют разрешенными. Пусть n=3 , кодовые комбинации: 000, 001, 010, 100, 110, 111, 101. Любая одиночная ошибка в таком коде переводит заданную разрешенную комбинацию в другую разрешенную комбинацию. Это случай без избыточного кода, не обладающего корректирующей способностью. Если предположить, что d=2, и для n=3 сформируем набор разрешенных комбинаций: 000, 011, 101, 110 - разрешенные комбинации; 001, 010, 100, 111 - запрещенные комбинации. При этом однократная ошибка переведет кодовую комбинацию из категории разрешенных в категорию запрещенных. Этот факт позволяет обнаружить наличие ошибки. Эти ошибки будут обнаружены, если кратность их нечетная. При d=2 и более в кодах появляется корректирующее свойство. В общем случае при необходимости обнаружения ошибки с кратностью s очевидно, что Для исправления одиночной ошибки в разрешенной кодовой комбинации необходимо составить подмножества кодовых комбинаций, зная, в каком подмножестве запрещенных кодовых комбинаций окажется принятая, можно точно восстановить переданную комбинацию, т.е. исправить ошибки. Рассмотрим случай, когда d=3 и n=3.
100
  000 000
Тогда по принятой комбинации 011 и факту её попадания в запрещенную кодовую комбинацию ошибка будет обнаружена, а зная, что подмножество запрещенных комбинаций соответствует разрешенной комбинации 111, мы можем исправить принятую комбинацию на разрешенную. Код при этих условиях обладает свойствами исправления ошибок. В общем случае для обеспечения возможности исправления всех ошибок кратности до t включительно при декодировании при методе максимального правдоподобия, каждая из ошибок декодирования должна приводить к запрещенной комбинации, относящейся к подмножеству исходных разрешенных кодовых комбинаций:
Общая граница обнаружения и исправления ошибок с соответствующей кратностью:
Таким образом, задача построения помехоустойчивой корректирующей способностью сводится к обеспечению необходимого минимального кодового расстояния. Увеличение минимального кодового расстояния приводит к росту избыточности кода, при этом желательно, чтобы число проверочных символов было минимальным. Это противоречие разрешается через определение верхней и нижней границ числа проверочных символов. В настоящее время известен ряд границ, которые устанавливают взаимосвязь между кодовым расстоянием и числом проверочных символов. Кроме того, эти границы позволяют определить вероятность ошибки декодирования. Граница Хемминга находится из соотношения известного для числа разрешенных комбинаций:
Применение границы Хемминга дает результаты близкие к оптимальным для высокоскоростных кодов Для низкоскоростных кодов, т.е. R =
Граница Варшамова – Гильберта:
Таким образом, граница Хемминга и Плоткина определяют необходимое количество проверочных символов, а граница Варшамова- Гильберта достаточное их количество. Если количество проверочных символов выбрано так, что оно удовлетворяет эти границам, то код считается близким к оптимальному. Коды, в которых число проверочных символов выбирается равным границам Хемминга или Плоткина называется совершенным или полноупакованным.
5.3.Линейные (систематические) коды.
5.3.1.Механизмы кодирования и синдромного декодирования.
В линейных систематических кодах информационные символы при кодировании не изменяются, а проверочные символы получаются в результате суммирования по модулю 2 определенного числа информационных символов. Запишем некоторые разрешенные кодовые комбинации систематического кода (n, k) Тогда Обнаружение и исправление ошибок систематическим кодом сводится к определению и последующему анализу синдрома или вектора ошибок. Под синдромом понимают некую совокупность символов
Если при приеме информационных и проверочных символов (принятое считается полная кодовая комбинация, состоящая из информационных и проверочных символов) не произошло ошибок, то принятые вычисленные проверочные символы будут совпадать. В этом случае все разряды синдрома будут равны нулю. Таким образом, нулевой синдром соответствует случаю отсутствия ошибок. Если в принятых кодовых комбинациях есть ошибки, то в разрядах синдрома появятся 1. Это и есть способ обнаружения ошибок систематическим кодом, который лежит в основе синдромного декодирования. Если код имеет минимальное кодовое расстояние Процедура построения систематического кода, способного обнаруживать ошибки, сводится к выбору весовых коэффициентов Пусть требуется построить систематический код длиной n=7, способный исправлять одиночные ошибки, т.е.
Выберем r=3, следовательно, код (7,4)- совершенный и близкий к оптимальному. Тогда кодовая комбинация
Найдем весовые коэффициенты
000, 001, 010, 100, 011, 101, 110, 111
Если ошибки отсутствуют, то синдром должен быть нулевым. Допустим, что появление одной 1 в синдроме будет связано с ошибками в проверочных символах кодовой комбинации. Тогда 100 → ошибка в b1, 010→ ошибка в b2, 001→ ошибка в b3. Появление большего числа единиц в синдроме будет связано с ошибками в информационных символах. Теперь присвоим информационным символам с ошибками оставшиеся синдромы, причем в порядке возрастания их двоичных символов: 011→ ошибка в 101→ ошибка в 110→ ошибка в 111→ ошибка в Для определения коэффициентов их надо подобрать таким образом, чтобы при возникновении ошибки в информационном символе аi появлялся бы соответствующий этой ошибке синдром. Например, для ошибки в символе
Тогда по этим коэффициентам строятся уравнения формирования проверочных символов, которые будут иметь вид:
5.3.2. Матричное представление линейных (систематических) кодов. В матричной форме систематическое кодирование задается некоторой порождающей матрицей Gk×n. Тогда можно записать следующее соотношение: B1×n= A1×k • Gk×n, где B1× n= [ Порождающая матрица может быть представлена в следующем виде, если учесть, что для проверочных символов мы выбираем синдром с одной единицей, и использовать правило формирования проверочных символов, тогда: Gk×n= (Ik×k Pk×r), где Ik×k - единичная матрица по числу информационных символов; Pk×r - правило формирования проверочных символов. Заметим, что в матрице Pk×r включаются именно коэффициенты Для рассмотренного ранее примера порождающая матрица будет иметь вид:
Тогда можно определить любой вектор кодовой комбинации В по заданному вектору информационных символов А. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|





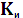 ;
;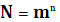
 .
.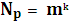
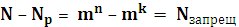
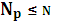
 в общем случае определяется выражением:
в общем случае определяется выражением: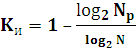
 - относительная скорость кода
- относительная скорость кода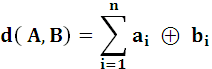

 - это минимальное расстояние между разрешенными кодовыми комбинациями данного кода.
- это минимальное расстояние между разрешенными кодовыми комбинациями данного кода.  является основной характеристикой корректирующей способности кода.
является основной характеристикой корректирующей способности кода.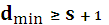 (граница обнаружения ошибки кратностью s).
(граница обнаружения ошибки кратностью s). 001
001 - граница исправления ошибок кратностью t.
- граница исправления ошибок кратностью t. .
. , где n=k+r – число символов; t =
, где n=k+r – число символов; t =  - кратность исправляемых ошибок;
- кратность исправляемых ошибок;  - число сочетаний из n по i.
- число сочетаний из n по i.
 > 0,3.
> 0,3. ≤ 0,3, границу числа проверочных символов называют границей Плоткина:
≤ 0,3, границу числа проверочных символов называют границей Плоткина: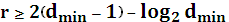

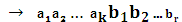 , где
, где  - информационные символы;
- информационные символы;  - проверочные символы.
- проверочные символы. , где
, где 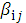 - некоторый коэффициент принимающий значение 0 или 1 в зависимости от того, участвует или нет данный информационный символ
- некоторый коэффициент принимающий значение 0 или 1 в зависимости от того, участвует или нет данный информационный символ  в формировании проверочного символа
в формировании проверочного символа  .
. сформированную, путем сложения по модулю 2 принятых проверочных символов и вычисленных проверочных символов. Вычисленные проверочные символы получаются из принятых информационных символов
сформированную, путем сложения по модулю 2 принятых проверочных символов и вычисленных проверочных символов. Вычисленные проверочные символы получаются из принятых информационных символов  по тому же правилу, которое используется для формирования проверочных символов.
по тому же правилу, которое используется для формирования проверочных символов.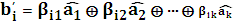
 , то такой код способен исправлять ошибки. Это значит, что по виду синдрома можно определить номер ошибочной позиции принятой кодовой комбинации.
, то такой код способен исправлять ошибки. Это значит, что по виду синдрома можно определить номер ошибочной позиции принятой кодовой комбинации.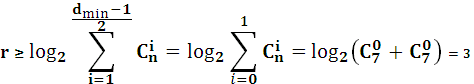
 - это и есть кодовая комбинация (7,4). Для нашего случая получим:
- это и есть кодовая комбинация (7,4). Для нашего случая получим: ,
, ,
, .
. ,
, ,
, ,
,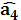 .
. =0,
=0, 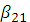 = 1,
= 1,  =1,
=1,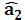 →
→  =1,
=1,  =0,
=0,  =1,
=1, →
→  =1,
=1,  =1,
=1,  =0,
=0, →
→ 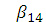 =1,
=1,  =1,
=1,  =1.
=1. ,
, ,
, .
.





















 ] - вектор-строка кодового слова; A1× k = [
] - вектор-строка кодового слова; A1× k = [  ] - вектор-строка информационного слова; Gk×n- порождающая матрица.
] - вектор-строка информационного слова; Gk×n- порождающая матрица. 1
1
 1
1