
|
|
Энтропия всегда неотрицательна.
2.Энтропия равна нулю в том крайнем случае, когда вероятность одного из событий равна 1.Это случай, когда о сообщении все известно и результат не приносит никакой информации.
0 0,5 p
Энтропия сообщения максимальна, если события равновероятны. Т.е., если Это свойство определяется в падении информации по Шеннону и по Хартли. В случае неравновероятности событий количество информации по Шеннону всегда меньше потенциальной информативной емкости. 4.Энтропия аддитивна. Пусть задано два сообщения A= C=
Кроме аксиом Шеннона, которые использовались для формулировки понятия энтропии, им были использованы специальные подходы. Подходы Шеннона к определению количества информации сообщения длиной L в условиях заданной вероятностной схемы сопровождается специальными требованиями: 1. Пустое сообщение не содержит информации.
2. Количество информации, содержащейся в сообщении, пропорционально его длине.
Если есть некоторое сообщение T длиной L символов некоторого алфавита А объемом n, то количество информации
Хинчен и Фадеев через задание своих аксиом показали, что энтропия конечной вероятностной схемы однозначно определяется с точностью до постоянного множителя.
Аксиомы Хинчена 1.Энтропия конечной вероятностной схемы ненулевая, непрерывная по вероятностям pi при условиях: 1. 2.
2.Энтропия, заданная конечной вероятностной схемой, симметрична по pi.
3. Энтропия, заданная конечной вероятностной схемой, при наличии пустого сообщения равна энтропии, заданная конечной вероятностной схемой без этого сообщения.
4.Энтропия объединенной вероятностной схемы:
5. Энтропия конечной вероятностной схемы при равновероятных событиях: Аксиомы Фадеева 1. 2. 3. При В дальнейшем все эти подходы Шеннона, Хинчена, Фадеева позволяют характеризовать производительность источника, оценивать возможности сжатия информации и анализировать пропускную способность канала.
2.3. Взаимная информация и её свойства. Условная энтропия. Для непрерывных величин Рассмотрим два связанных источника:
   С= С= 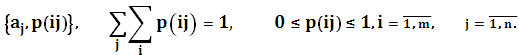
B=
Если два источника считать связанными друг с другом, то следует ожидать, что событие одного источника позволяют делать некоторые предположения о событиях другого. В терминах теории информации это означает, что неопределенность второго источника снижается, т.е. источники обмениваются взаимной информацией. Известно, что для совместных событий между собственной, условной и совместной вероятностями существует зависимость, имеющая вид:
Прологарифмируем данное выражение:
Из полученных выражений видно, что собственная информация пары событий
Если взять I(A;B)= Свойства взаимной информации. 1. Взаимная информация положительна. 2. Взаимная информация симметрична относительно пары вероятностных схем. I(А;B)=I(B;A)
3. Если сообщение A и B – независимы, т.е. не совместны, то взаимная информация I(А;B)=0. Если сообщения A и B полностью зависимы, а именно совпадают, т.е. A и B содержат одну и ту же информацию, то взаимная информация:
I(А;B)=I(A)+I(B)
Пример. Если A и B рассматривать как сообщение, порожденные различными источниками (например, публикации в различных газетах ), тогда для получения взаимно большей совместной ( суммарной) информации взаимная, т.е. одинаковая в данном случае информация, должна быть минимальной. Если A и B сообщения соответственно на входе и выходе канала связи с помехами, то для получения взаимно большей информации её получателем необходимо, чтобы взаимная информация была наибольшей. В то же время для описания воздействия помех в канале связи на полученное сообщение используется понятие условной информации и условной энтропии. Для определения условной информации и условной энтропии в заданной объединенной вероятностной схеме вернемся к соотношению:
При этом совместная информация пары событий складывается из собственной информации каждого из этих событий и некоторой информации, добавленной вторым событием при условии, что произошло первое событие. Поэтому
тогда математическое ожидание этой случайной величины и будет являться условной энтропией объединенной вероятностной схемы:
Найдем соотношение между условной энтропией и ее взаимной информаций:
Рассмотрим взаимную информацию опять как случайную величину и, усредняя её, т.е. определяя математическое ожидание по объединенной вероятностной схеме, получим: I(А;B) = E
2.4 Понятие совместной энтропии. Для двух источников, образующих объединенную вероятностную схему, используя понятие совместной вероятности пары событий, можно определить среднюю информацию всех пар событий: H(AB) = E Не сложно показать, что совместная энтропия складывается из: H(AB)=H(A)+H(A/B)=H(B)+H(B/A). Если источники не совместны, то: H(A/B)=H(A), H(B/A)=H(B). Если источники считаются связанными, тогда: H(A/B) H(B/A) Поэтому в общем случае совместная энтропия определяется следующим образом: H(AB)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
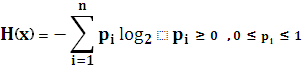
 H(p)
H(p)



 1 H0
1 H0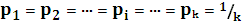 , то
, то  .
. и B=
и B=  .
.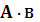 , A и B являются независимыми и составляют полную группу, т.е.
, A и B являются независимыми и составляют полную группу, т.е. 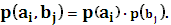
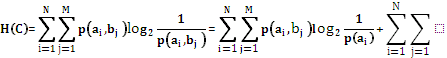
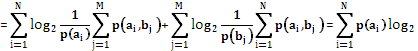
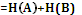
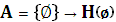 =0
=0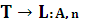 , то
, то  .
. .
. , C
, C  .
. ;
; .
.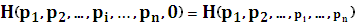
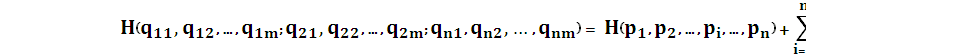 , где
, где  ,
, 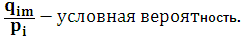
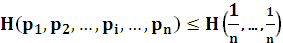
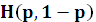 – непрерывна при условиях:
– непрерывна при условиях:  и положительна хотя в одной точке.
и положительна хотя в одной точке. - симметрична по
- симметрична по  .
.
 где
где  .
. .
.

 A=
A= 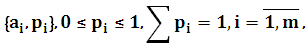
 .
.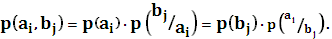
 =
= 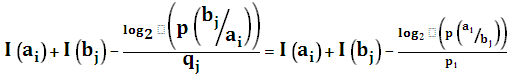 .
.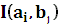 определяется суммой собственных информаций каждого из событий за вычетом некоторой неотрицательной величины, которая снижает неопределенность, т.е. она сама в свою очередь является информацией. Эту величину называют взаимной информацией пары событий:
определяется суммой собственных информаций каждого из событий за вычетом некоторой неотрицательной величины, которая снижает неопределенность, т.е. она сама в свою очередь является информацией. Эту величину называют взаимной информацией пары событий: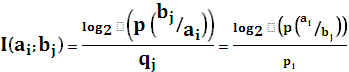 .
.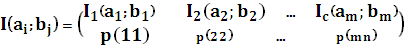 , тогда для этой случайной величины можно использовать понятие математического ожидания.
, тогда для этой случайной величины можно использовать понятие математического ожидания.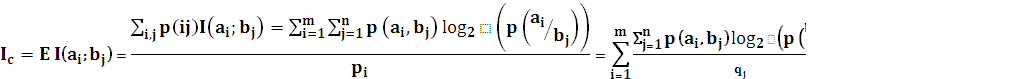
 =
=  =
= 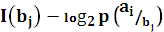 .
. I
I  называют условной информацией пары случайных событий. Если аналогично тому, как мы это делали ранее, составить вероятностную схему для условной вероятности пары событий как для случайной величины:
называют условной информацией пары случайных событий. Если аналогично тому, как мы это делали ранее, составить вероятностную схему для условной вероятности пары событий как для случайной величины: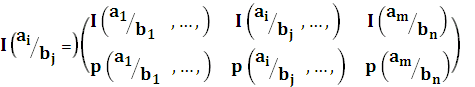 ,
,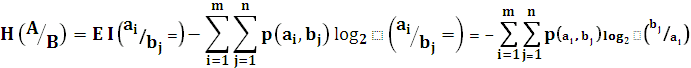

 H(A) - H(A/B) = H(B) - H(B/A).
H(A) - H(A/B) = H(B) - H(B/A). .
. H(A);
H(A);