|
|
Алгоритм Блейка-Порецкого.Начало. Задана произвольная ДНФ булевой функции. Шаг 1. Построим список троичных векторов, представляющих конъюнкции ДНФ. Удалим из списка все векторы, поглощаемые другими. Если останется лишь один вектор, пойдем на конец. Иначе обозначим второй из оставшихся векторов через α. Шаг 2. Найдем для вектора α очередной смежный вектор β среди векторов, расположенных в списке выше α. Если такого вектора β нет, то идем на шаг 5. Иначе обобщенно склеим а и β и полученный вектор γ припишем к списку последним. Шаг 3. Если вектор γ поглощается хотя бы одним вектором из списка, то удалим γ (в частном случае γ может совпадать с одним из векторов списка, тогда удалим именно приписанный вектор γ, иначе произойдет "зацикливание" алгоритма, так как вектор γ будет вновь появляться в списке) и идем на шаг 2. Если вектор γ не поглощается, то удалим все векторы, поглощаемые им. Шаг 4. Если вектор α не удален, то идем на шаг 2. Шаг 5. Если вектор α удален, но был не последним в списке, то выберем в качестве нового α следующий по списку вектор и вернемся на шаг 2. Конец. Векторы, оставшиеся в списке, задают сокращенную ДНФ исходной функции. Алгоритм Блейка-Порецкого отличается от алгоритма Квайна-МакКласки прежде всего тем, что оперирует с произвольной ДНФ, в то время как алгоритм Квайна-МакКласки требует на входе совершенную ДНФ. Конечно, можно перейти от произвольной ДНФ к совершенной, но она может оказаться очень длинной, и применение алгоритма Квайна-МакКласки станет неэффективным. [24, 25] Определение. Булевой матрицей назовем матрицу, элементами которой являются булевы константы (другими словами, строками и столбцами которой являются булевы векторы). Прежде всего рассмотрим, как в явном виде показать, используя булеву матрицу, из каких точек функции состоят ее максимальные интервалы. Определение. Таблицей Квайна булевой функции f(x1,..., хn) назовем булеву матрицу, строкам которой поставим в соответствие конъюнкции сокращенной ДНФf (все максимальные интервалы функции), а столбцам - конъюнкции совершенной ДНФf (все точки). Элемент матрицы, стоящий на пересечении i-й строки и j-то столбца, положим равным единице тогда и только тогда, когда i-я конъюнкция сокращенной ДНФ поглощает j-ю конъюнкцию совершенной ДНФ (i-й максимальный интервал функции содержит ее j-ю точку). Определение.Будем говорить, что строка таблицы Квайна покрывает столбец, если она содержит единицу в этом столбце. Любое покрытие таблицы Квайна функции f(x1,..., хп) задает подмножество максимальных интервалов, достаточное для функции, так как каждая точка функции принадлежит хотя бы одному из ее максимальных интервалов. Другими словами, любое покрытие таблицы Квайна задает ДНФf. В частности, покрытие, состоящее из всех строк таблицы, задает сокращенную ДНФ. Определение.Длиной покрытия назовем количество строк, образующих покрытие. Определение. Покрытие таблицы Квайна называется безызбыточным, если при удалении из него хотя бы одной строки оно перестает быть покрытием. Определение.Кратчайшим покрытием таблицы Квайна назовем покрытие минимальной длины. Определение.Рангом, строки таблицы Квайна назовем ранг приписанной ей простой импликанты. Определение. Минимальным покрытием таблицы Квайна назовем покрытие с минимальной суммой рангов строк. Определение.Столбец булевой матрицы назовем ядерным, если он содержит ровно одну единицу. Строку булевой матрицы назовем ядерной, если она покрывает ядерный столбец. Правило ядерной строки. Если в матрице есть ядерная строка, то она включается в любое искомое покрытие и удаляется из матрицы вместе со всеми столбцами, которые ядерная строка покрывает. Удаляются также пустые строки (целиком состоящие из нулей), которые при этом могут появиться. Начало.Задана булева матрица. Шаг 1. Применим к матрице правило ядерной строки многократно, пока это возможно. Если матрица стала пустой, то идем на конец. Иначе из равных столбцов оставим по одному, пронумеруем столбцы упрощенной матрицы и припишем строкам булевы переменные s1,...,sm. Шаг 2. Выберем очередной (j-й) столбец матрицы. Если столбцы исчерпаны, идем на шаг 3. Иначе построим дизъюнкцию Dj переменных, приписанных строкам, содержащим единицы в j-м столбце, и возвратимся на шаг 2. Шаг 3. Из полученных дизъюнкций построим конъюнктивную нормальную форму D1· ...·Dk Шаг 4. Раскроем скобки в КНФ, выполняя поглощения конъюнкций. Получим ДНФ=K1 v...v Kt. Конец. Конъюнкции K1,..,Kt задают все безызбыточные покрытия упрощенной на первом шаге матрицы. Добавив к каждому из них ядерные строки (выделенные на первом шаге), получим все безызбыточные покрытия исходной матрицы.
Поискминимальных и кратчайших покрытий Зная все безызбыточные покрытия матрицы, выбрать из них кратчайшие или минимальные не составляет труда. Однако поиск всех безызбыточных покрытий булевой матрицы становится излишне трудоемким, если требуется найти одно кратчайшее покрытие. В этом случае можно ограничиться поиском только некоторых безызбыточных покрытий, лишь бы среди них содержалось хотя бы одно кратчайшее. И тогда применимы следующие два правила упрощения булевой матрицы. Правило строки-предшественницы. Если в булевой матрице есть такие строки а и β, что а≤ β, то строка-предшественница а удаляется из матрицы (при этом кратчайшее покрытие не теряется, так как в любом покрытии строку а можно заменить строкой β, и оно останется покрытием). Правило столбца-последователя.Если в булевой матрице есть такие столбцы γ и δ, что γ ≤ δ, то столбец-последователь δ удаляется из матрицы (так как любое покрытие столбца γ одновременно покрывает столбец δ). Заметим, что удаление столбцов-последователей может привести к появлению строк-предшественниц, и наоборот, поэтому эти два правила стоит выполнять "циклически" друг за другом. Определение.Булеву матрицу, не содержащую ни ядерных строк, ни строк-предшественниц, ни столбцов-последователей, назовем циклическим остатком. [25] Алгоритм поиска одного кратчайшего покрытия булевой матрицы(основан на построении циклического остатка и поиске всех его безызбыточных покрытий). Начало. Задана булева матрица. Шаг 1. Если в матрице есть однострочное покрытие, то включим его в покрытие, идем на конец. Шаг 2. Применим правило ядерной строки. Если ядерная строка обнаружилась, идем на шаг 1. Шаг 3. Применим правило строки-предшественницы. Если такая строка обнаружилась, идем на шаг 2. Шаг 4. Применим правило столбца-последователя. Если такой столбец обнаружился, идем на шаг 3. Шаг 5. Построим КНФ функции покрытия полученного циклического остатка и преобразуем КНФ в ДНФ, раскрывая скобки и выполняя поглощения. Шаг 6. Конъюнкция минимального ранга полученной ДНФ задает кратчайшее покрытие циклического остатка. Добавим к этому покрытию ядерные строки, выделенные на шаге 2. Конец. Получено кратчайшее покрытие исходной матрицы. 26. Частичные булевы функции, способы их задания, доопределение Определение. Неполностью определенной (частичной) булевой функцией fх(x1,... ,xn) назовем однозначное отображение подмножества M булева пространства Bn в булево множество B, т.е. Как видно из определения, частным случаем неполностью определенной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией. Неполностью определенная булева функция может быть задана различными способами, аналогичными способам задания булевой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами. 1) Задание неполностью определенной булевой функции таблицей истинности.В левой части таблицы истинности представляются, как и раньше, все векторы булева пространства, а в ее правой части либо перечисляются значения функции, либо указывается специальный символ х (если набор в область определения не входит). 2) Задание неполностью определенной булевой функции характеристическими множествами.Кдвум известным нам характеристическим множествам 3) Задание неполностью определенной булевой функции матрицей Грея.В матрице Грея тем же символом х отмечаются клетки, не входящие в область определения. Неполностью определенная булева функция не может быть задана формулой, так как значение формулы может быть вычислено на всех наборах из Bn.
Определение. Доопределением неполностью определенной булевой функции fх(x1,...,xn) назовем любую булеву функцию f(x1,..., xn), удовлетворяющую условиям:
Это означает, что значения любого доопределения должны совпадать со значениями неполностью определенной булевой функции fх(x1,... ,xn) на наборах из характеристических множеств Утверждение о числе доопределений.Число различных доопределений неполностью определенной булевой функции Пример.
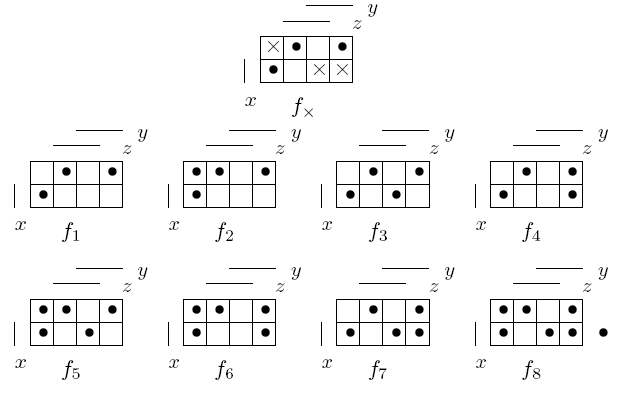
27.Частичные булевы функции, точный метод их минимизации Определение. Неполностью определенной (частичной) булевой функцией fх(x1,...,xn) назовем однозначное отображение подмножества M булева пространства Bn в булево множество B, т.е. Как видно из определения, частным случаем неполностью определенной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией. Неполностью определенная булева функция может быть задана различными способами, аналогичными способам задания булевой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами. Определение. Минимизировать неполностью определенную булеву функцию - это значит выбрать среди кратчайших ДНФ всех ее доопределений самую короткую ДНФ. Пример.Для рассмотренной в предыдущем примере (26 билет) неполностью определенной булевой функции fх(x, y, z) перебор кратчайших ДНФ всех восьми доопределений приводит к следующему результату: самой короткой оказывается кратчайшая ДНФ доопределения f6(x,y,z).
Таким образом, тот факт, что неполностью определенная булева функция задается не на всем булевом пространстве, а лишь на его подмножестве, мы используем для такого "выгодного" доопределения функции, которое приводит к наиболее короткой ДНФ и к наиболее простой схеме, реализующей функцию. Конечно, как и в случае булевых функций, возможны другие постановки задачи минимизации неполностью определенных булевых функций - можно, например, искать ее приближенную кратчайшую ДНФ. Определение.Интервал I назовем допустимым для неполностью определенной булевой функции fх(x1,..., xn), если он удовлетворяет условиям: Определение.Интервал I назовем максимальным для неполностью определенной булевой функции, если он допустим для этой функции, и не существует другого допустимого для нес интервала I' такого, что Пример.На левой матрице Грея изображены два недопустимых интервала
28. Частичные булевы функции, их минимизация по матрицам в коде Грэя. Метод Закревского Определение. Неполностью определенной (частичной) булевой функцией fх(x1,... ,xn) назовем однозначное отображение подмножества M булева пространства Bn в булево множество B, т.е. Как видно из определения, частным случаем неполностью определенной булевой функции является булева функция: ее областью определения является все булево пространство. Булеву функцию также называют полностью определенной булевой функцией. Неполностью определенная булева функция может быть задана различными способами, аналогичными способам задания булевой функции, в частности, таблицей истинности, матрицей Грея и характеристическими множествами. Для нахождения всех максимальных интервалов неполностью определенной функции fх(x1,..., xn) можно применить алгоритм Квайна-Мак-Класки или алгоритм Блейка-Порецкого к ее доопределению f(x1,...,xn), которое удовлетворяет условию: Алгоритм поиска кратчайшей ДНФ неполностью определенной булевой функции(основан на нахождении всех максимальных интервалов функции, построении таблицы Квайна и поиске кратчайшего покрытия этой таблицы). Начало. Задана частичная булева функция fх(x1,..., xn). Шаг 1. Находим любым алгоритмом все максимальные интервалы функции fх(x1,..., xn). Шаг 2. Строим таблицу Квайна функции fx(x1, . . . ,xn). Шаг 3. Находим кратчайшее покрытие таблицы Квайна, а по покрытию - кратчайшую ДНФ функции fх(x1,..., xn). Конец.
Алгоритм Закревского(ориентирован на матричное представление функции и визуальный способ решения). Начало. Задана матрица Грея неполностью определенной булевой функции fх(x1,...,xn). Шаг 1. Для каждой точки вычислим цену - количество соседних ей векторов из множества Шаг 2. Среди неотмеченных точек рассмотрим точку минимальной цены и найдем все максимальные интервалы, которым она принадлежит. Выберем из них тот максимальный интервал, который содержит наибольшее число неотмеченных точек. Если таких интервалов несколько, то выберем из них интервал максимальной мощности. Шаг 3. Включим выбранный интервал в решение и отметим его точки. Если не все точки отмечены, то идем на шаг 2. Конец. Включенные в решение интервалы задают приближенную кратчайшую ДНФ функции
29. Метод конкурирующих интервалов для минимизации частичной булевой функции. Метод конкурирующих интервалов. Этот метод поиска приближенной кратчайшей ДНФ неполностью определенной булевой функции не ориентирован на ее представление матрицей в коде Грея, а значит, может применяться к булевой функции большого числа переменных. Перед изложением метода введем необходимые определения. Рассмотрим частичную булеву функцию fх(x1,..., xn), ее точку α и допустимый интервал I. Определение.Минимальным расширением интервала I до точки α (обозначается [I,α]) называется интервал I' минимальной мощности, удовлетворяющий условиям: Как следует из определения, интервал [I, α] строится так: - внутренние компоненты интервала I остаются внутренними и в интервале [I, α], - внешние компоненты интервала I сохраняют свое значение в интервале [I, α], если они совпадают с соответствующими компонентами α, - внешние компоненты интервала I становятся внутренними в интервале [I, α], если они ортогональны соответствующим компонентам α. Пример.
Определение.Интервал I и точка α называются совместимыми, если интервал [I,α] является допустимым для функции fх (xi, . . . , xn). Перейдем теперь к изложению метода конкурирующих интервалов. Метод является итерационным. На каждой итерации метода имеется некоторое частичное решение поставленной задачи, которое улучшается по определенным правилам. В данном случае частичным решением является множество допустимых интервалов функции. На каждой итерации будем изменять решение, либо добавляя в него новый интервал, либо расширяя один из имеющихся интервалов. При этом желательно как можно меньше изменять частичное решение, то есть добавлять интервал наименьшей мощности или расширять интервал по наименьшему числу компонент. Пусть на k-й итерации имеются частичное решение Uk и множество Mk точек функции, не содержащихся ни в одном интервале из Uk (на первой итерации Пусть строка α матрицы совместимости не содержит единиц. Это означает, что в множестве Uk нет ни одного интервала, совместимого с точкой α, то есть ни один интервал не может быть расширен на множестве Правило строки без единиц. Если в матрице совместимости есть строка, не содержащая ни одной единицы, то она удаляется из матрицы. В матрицу добавляется столбец, которому сопоставляется вектор из удаленной строки. Правило столбца без единиц. Если в матрице совместимости есть столбец, не содержащий ни одной единицы, то он удаляется из матрицы. Интервал из удаленного столбца расширяется до максимального и добавляется в окончательное решение. Правило столбца с одной единицей. Если в матрице совместимости есть столбец I, содержащий ровно одну единицу (в строке α), то эта строка удаляется из матрицы, а интервал I заменяется на интервал [I, α]. Определение. Рангом столбца матрицы совместимости назовем ранг сопоставленного столбцу интервала. Правило столбца наибольшего ранга. Если к матрице совместимости не применимо ни одно из трех предыдущих правил, то в ней выбирается столбец I наибольшего ранга. Среди совместимых с ним точек находится точка α с минимальным числом компонент, ортогональных внешним компонентам интервала I. Из матрицы удалются строки, которым сопоставлены точки из [I, α]. Интервал I заменяется на [I, α] и столбец I пересчитывается.
30.Система булевых функций. Кратчайшая и безызбыточная системы ДНФ. Определение.Множество булевых функций,
зависящих от одних и тех же переменных и рассматриваемых как единый объект, называется системой булевых функций. Система булевых функций может рассматриваться как математическая модель дискретного устройства. В этом случае ставится задача построения схемы из логических элементов, реализующей эту систему функций. Определение. Длиной системы ДНФ называется число различных конъюнкций, входящих во все ДНФ системы. Определение. Рангом системы ДНФ называется сумма рангов различных конъюнкций, входящих во все ДНФ системы. Пример.Рассмотрим систему ДНФ.
В ДНФ системы входят шесть различных конъюнкций, сумма их рангов равна 15. Значит, длина этой системы 6, ранг 15. Определение.Кратчайшей системой ДНФ (Dкрат) системы булевых функций Определение. Безызбыточной системой ДНФ(Dбез) системы булевых функций - удаление любой конъюнкции K из любой ДНФ Di приводит к тому, что Di перестает задавать функцию fi(x1,... ,xn), - если конъюнкция K входит в ДНФ Di1,...,Dik, то удаление любой буквы из K приводит к тому, что по крайней мере одна из этих ДНФ Понятно, что система безызбыточных ДНФ будет также и безызбыточной системой ДНФ, обратное же не всегда верно.
31. Получение приближенной кратчайшей системы ДНФ методом конкурирующих интервалов. Определение. Минимизировать систему булевых функций это значит построить ее кратчайшую систему ДНФ. Конечно, как и в случае одной булевой функции, возможны и другие постановки задач: построить все кратчайшие системы ДНФ, систему наименьшего ранга и так далее. Кроме того, так как минимизация системы булевых функций более сложна, чем минимизация одной функции, часто на практике строится приближенная кратчайшая система ДНФ, то есть система ДНФ, близкая по длине к кратчайшей. Кроме того, часто ставится задача построения безызбыточной системы ДНФ. Это связано как с тем, что безызбыточные системы ДНФ часто оказываются близкими по длине к кратчайшим, так и с тем, что схемы, построенные по безызбыточным системам ДНФ, удобны для диагностики. Как было показано ранее, кратчайшая система ДНФ и система кратчайших ДНФ не являются равнозначными понятиями. Поэтому при минимизации системы булевых функций все функции необходимо рассматривать как единый объект. Как правило, для решения этой задачи модифицируются методы минимизации одной булевой функции. Рассмотрим метод конкурирующих интервалов в применении к системе булевых функций. Во-первых, точки и интервалы сопровождаются обозначениями или номерами функций. Так, запись α(1) означает точку α функции f1(x1,..., xn), а запись I(1, 3) - интервал I, допустимый для функций f1(x1,..., xn) и f3(x1,..., xn) и включенный в достаточное множество этих функций. Во-вторых, расширение интервала I(j1, . . . ,jk) до точки α(i) сопровождается номерами функций (i, j1,..., jk). В-третьих, интервал I(j1, . . ., jk) и точка α(i) совместимы, если и только если интервал I'(i,j1, ...,jk) = [I(j1, . . .,jk),α(i)] допустим для функции fi(x1, . . . , xn), fj1 (x1, . . . , xn),. . ., fjk (x1,...,xn). Пример.Рассмотрим систему F из предыдущих примеров.
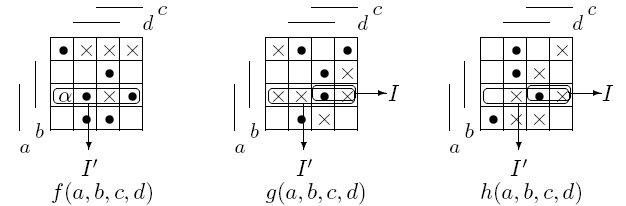
Рассмотрим точку α(f) = 1100 и интервал I(g,h) = 111-. Минимальное расширение интервала I(g,h) до точки α(f) (интервал I'(f,g,h) = 11 ) не является допустимым для функции h(a, b, c, d) и, следовательно, не может быть включен в решение. Однако если рассмотреть интервал I(g) = 111- и ту же точку α(f), то интервал I'(f,g) = [I(g),α(f)] = 11-- будет допустимым для функций f(a, b, c, d), g(a, b, c, d) и может быть включен в решение для этих функций. В-четвертых, интервал I(j1,... ,jk) при применении правила столбца без единиц расширяется так, чтобы он оставался допустимым для всех функций fj1(x1,...,xn),..., fjk(x1,...,xn).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.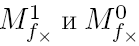 добавляатся третье,
добавляатся третье, 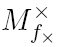 , состоящее из наборов, на которых функция не определена (для задания функции достаточно указать любые два из трех множеств).
, состоящее из наборов, на которых функция не определена (для задания функции достаточно указать любые два из трех множеств).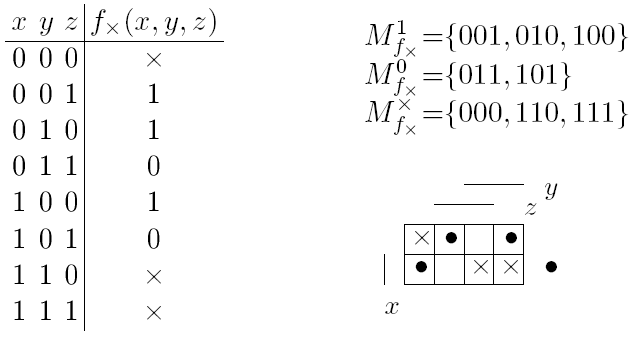

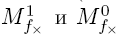 , и, в то же время, доопределение может принимать любые значения на наборах из множества
, и, в то же время, доопределение может принимать любые значения на наборах из множества 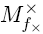 . Из этого и из теоремы о числе векторов с очевидностью следует утверждение.
. Из этого и из теоремы о числе векторов с очевидностью следует утверждение.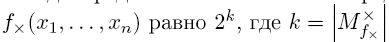
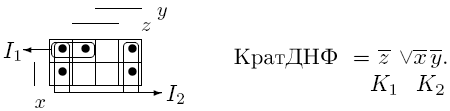
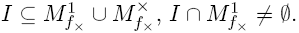

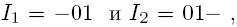 на средней – допустимый интервал I = -00 (но не максимальный), на правой - максимальный I' =--0.
на средней – допустимый интервал I = -00 (но не максимальный), на правой - максимальный I' =--0.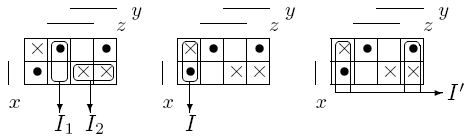
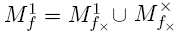 , а затем исключить из найденных интервалов те, которые не содержат ни одной точки функции fх(x1,..., xn). Таблица Квайна неполностью определенной функции fx(x1,... ,xп) строится аналогично таблице Квайна булевой функции.
, а затем исключить из найденных интервалов те, которые не содержат ни одной точки функции fх(x1,..., xn). Таблица Квайна неполностью определенной функции fx(x1,... ,xп) строится аналогично таблице Квайна булевой функции.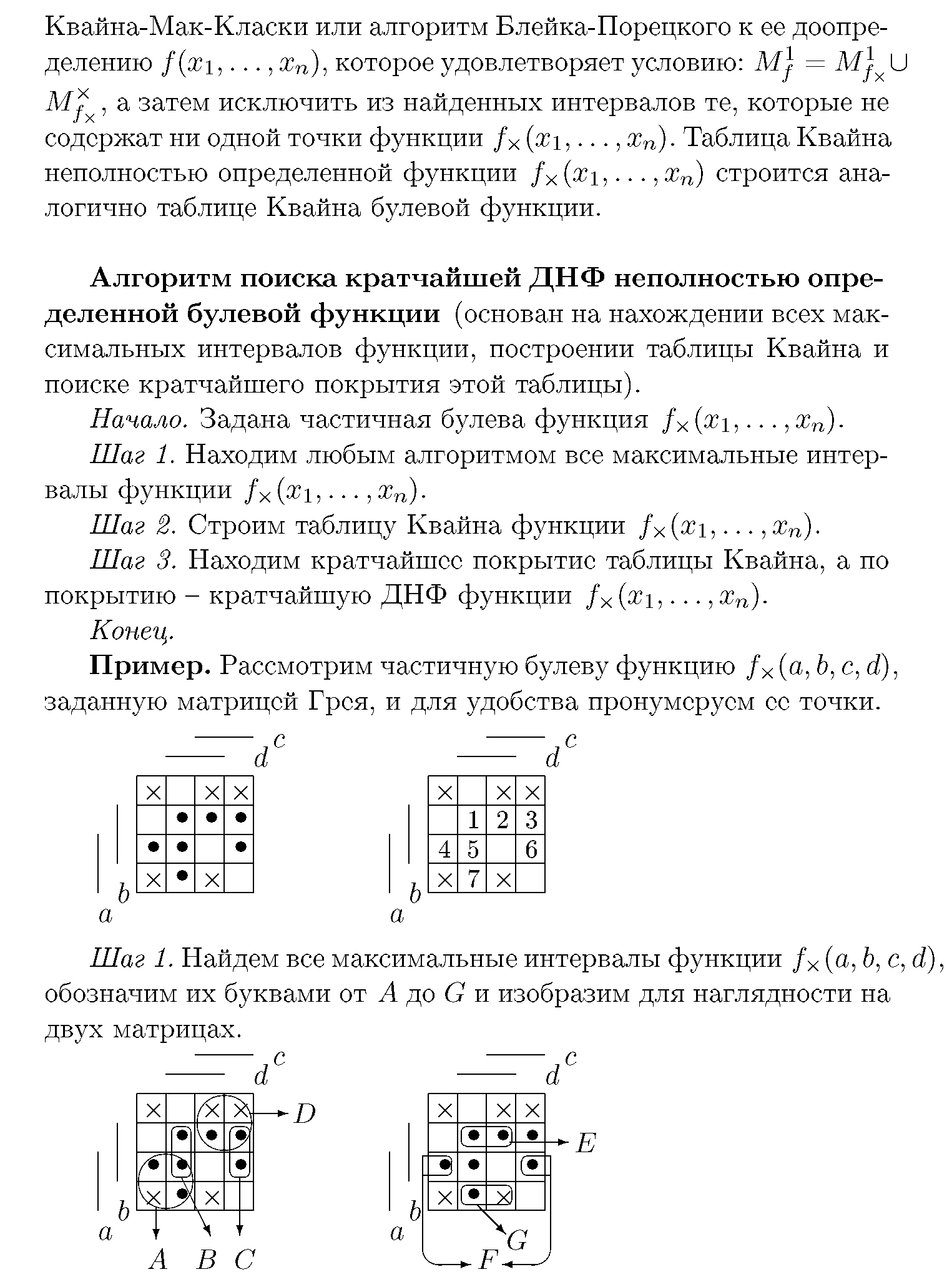
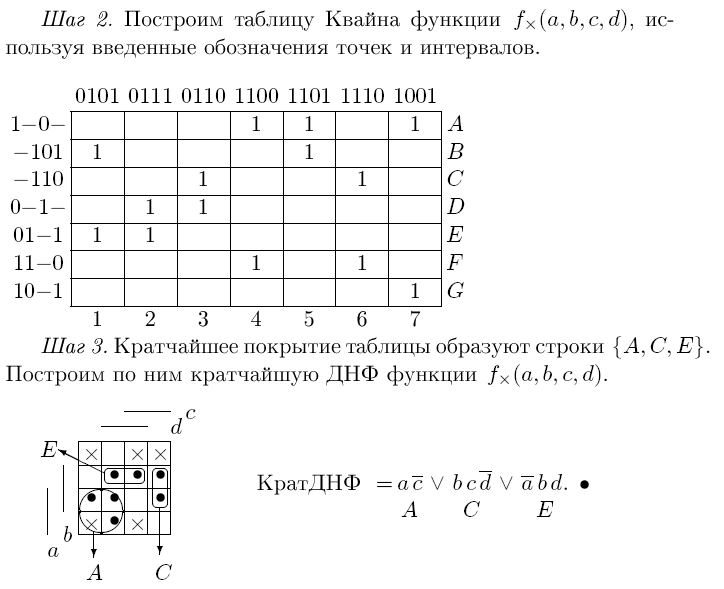
 . Все точки будем считать неотмеченными.
. Все точки будем считать неотмеченными.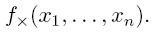
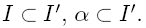

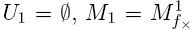 ). Построим булеву матрицу совместимости Rk, строкам которой сопоставим точки из Mk, а столбцам - интервалы из Uk. Элемент, стоящий на пересечении i-й строки и j-ro столбца, равен единице, если i-я точка совместима с j-м интервалом. Далее будем обозначать строки и столбцы матрицы совместимости символами сопоставленных им точек и интервалов.
). Построим булеву матрицу совместимости Rk, строкам которой сопоставим точки из Mk, а столбцам - интервалы из Uk. Элемент, стоящий на пересечении i-й строки и j-ro столбца, равен единице, если i-я точка совместима с j-м интервалом. Далее будем обозначать строки и столбцы матрицы совместимости символами сопоставленных им точек и интервалов.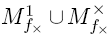 так, чтобы расширение включало точку α. Значит, в множество Uk следует добавить интервал, совместимый с α. Такой интервал наименьшей мощности это сама точка. Отсюда вытекает следующее правило.
так, чтобы расширение включало точку α. Значит, в множество Uk следует добавить интервал, совместимый с α. Такой интервал наименьшей мощности это сама точка. Отсюда вытекает следующее правило.
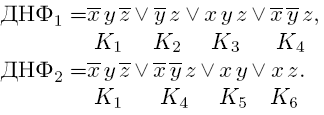
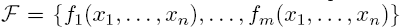 называется система ДНФ наименьшей длины из всех систем ДНФ, задающих систему F.
называется система ДНФ наименьшей длины из всех систем ДНФ, задающих систему F.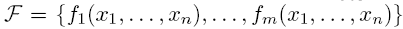 называется система
называется система  такая, что:
такая, что: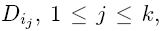 перестает задавать функцию fij (x1, . . . , xn).
перестает задавать функцию fij (x1, . . . , xn).