|
|
Утверждение о единственности СовДНФЛюбая булева функция, кроме константы 0, представима совершенной дизъюнктивной нормальной формой, единственной для данной функции. Алгоритм построения СовДНФ (по таблице истинности) вытекает из определения СовДНФ и состоит в циклическом выполнении следующих шагов: Шаг 1: в векторе – столбце значений функции выбирается очередная единица. Если единицы исчерпаны, то идем на конец. Шаг 2: по набору значений аргументов выбранной строки формируется конъюнкция всех аргументов с соблюдением следующего правила: если i – я компонента набора 0, то i – я переменная входит в конъюнкцию в степени 0 (с инверсией), иначе – в степени 1 (без инверсии). Полученная конъюнкция добавляется в формулу как очередное слагаемое. Идем на шаг 1. Конец.
Соединив полученные конъюнкции знаками дизъюнкции, получим:
14) Получение СовКНФ из разложения функции по переменным. Утверждение о существовании и единственности СовКНФ. Алгоритм построения СовКНФ по таблицк истинности. Пусть дана функция f(x1, x2, ... , xn). Представим ее инверсию СовДНФ:
Инвертируем обе части этого равенства: По законам двойного отрицания и де Моргана имеем: [заметив, что
Определение.Совершенная дизъюнктивная нормальная форма функции f(x1, x2, ... , xn), или СовКНФ, — это формула вида: Сформулируем утверждение с очевидностью вытекающее из СовКНФ. Утверждение о единственности СовКНФ Любая булева функция, кроме константы 1, представима cовершенной конъюнктивной нормальной формой, и она единственна для данной функции. Алгоритм построения СовКНФ по таблице истинности вытекает из определения СовКНФ и состоит в циклическом выполнении следующих шагов: Шаг 1: в векторе - столбце значений функции выбирается ноль. Если нули исчерпаны, то идем не конец. Шаг 2: по набору значений аргументов выбранной строки формируется дизъюнкция всех аргументов с соблюдением следующего правила: если i-я компонента набора равна 0, то i-я переменная входит в дизъюнкцию в степени 1 (без инверсии), иначе – в степени 0 (с инверсией). Полученная дизъюнкция добавляется в формулу как очередной сомножитель. Идем на шаг 1. Конец. Пример.
Соединив полученные дизъюнкции знаками конъюнкции, имеем:
15) Двойственная функция и двойственная формула.Принцип двойственности. Определение.Булева функция f*(x1, ...,xn) называется двойственной булевой функции f(x1,..., хп), если она получена из функции f(x1, ...,хп) инверсией всех аргументов и самой функции, т.е.
Определение.Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций. Теорема(принцип двойственности.) Если формула F задает булеву функцию f(x1, ...,xn), то двойственная ей формула F* задает двойственную функцию f*(x1, ...,xn). Пример.Рассмотрим формулу
16) Двойственная функция. Построение двойственной функции по таблице истинности. Определение.Булева функция f*(x1, ...,xn) называется двойственной булевой функции f(x1,..., хп), если она получена из функции f(x1, ...,хп) инверсией всех аргументов и самой функции, т.е.
Алгоритм построения таблицы истинности двойственной функции(основан на определении двойственной функции). Инверсия всех переменных превращает наборы в их антиподы. Поскольку в таблице истинности антипод первого набора расположен последним, антипод второго набора - предпоследним и так далее, то для построения функции Пример.Построим функцию, двойственную импликации.
17) Элементарная конъюнкция.Ортогональные, соседние и смежные конъюнкции Пусть имеем множество переменных X = {x1,x2, ...,xn}. Определение. Элементарной конъюнкцией назовем конъюнкцию переменных множества X, в которую каждая переменная входит не более одного раза (с инверсией или без инверсии). Примеры.Пусть X = {x1,x2,x3,x4}, тогда Определение.Две конъюнкции называются ортогональными по переменной xi, если эта переменная входит в одну конъюнкцию с инверсией, а в другую без инверсии. Пример.Конъюнкции Определение. Две конъюнкции называются соседними, если они ортогональны по одной и только одной переменной xi и совпадают по остальным. Пример.Конъюнкции Определение.Две конъюнкции называются смежными, если они ортогональны по одной и только одной переменной xi . Пример.Конъюнкции
18) Утверждение о конъюнкции и интервале. ДНФ и достаточное множество интервалов Утверждение о конъюнкции и интервале.Каждая элементарная конъюнкция K ранга r может быть задана интервалом IK ранга r следующего вида: если переменная xi не входит в K, то i-я компонента интервала IK является внутренней; иначе i-я компонента является внешней, она равна 0, если переменная xi входит в конъюнкцию K с инверсией, и равна 1, если переменная xi входит в K без инверсии. ДНФ и достаточное множество интервалов: Рассмотрим ДНФf = К1 V ... V Кm. По определению дизъюнкции, булева функция f(x1, ...,xn) принимает значение 1 тогда и только тогда, когда хотя бы одна из конъюнкций К1,..., Кm принимает значение 1. Это означает, что соответствующие интервалы I1,..., Im образуют множество, достаточное для функции f(х1, ...,хn). Таким образом и в этом случае можно пользоваться двумя "параллельными" языками: языком ДНФ и языком интервалов. Последний оказывается наиболее наглядным при задании булевых функций матрицами Грея. 19) Импликанты и простые импликанты функции Рассмотрим булевы функции f(x1, ...,xn) и g(x1, ...,xn). Определение.Булева функция g(x1, ...,xn) называется импликантой функции f(x1, ...,xn), если Так как x → у = 0 только на наборе 10, то для того, чтобы функция g(x1, ...,xn) была импликантой функции f(x1, ...,xn) достаточно, чтобы на всех тех наборах α, на которых g(α) = 1, функция f(x1, ...,xn) также принимала значение 1. Определение.Элементарная конъюнкция К называется простой импликантой функции f(x1, ...,xn), если она является импликантой этой функции, и не существует другой конъюнкции К', которая является импликантой функции f(x1, ...,xn) и поглощает конъюнкцию К. Другими словами, простая импликанта функции - это такая импликанта-конъюкция, которая не может быть упрощена выбрасыванием из нее переменных, то есть неупрощаемая конъюнкция. Это означает, что всякая простая импликанта К булевой функции f(xi,...,xn) задается максимальным для этой функции интервалом IK. 20) Cокращённая, кратчайшая, минимальная и безызбыточная ДНФ Определение.ДНФ, состоящая из всех простых импликант булевой функции f(x1, ...,xn), называется сокращенной ДНФ этой функции (СокрДНФf). Определение.Кратчайшей ДНФ (КратДНФf) булевой функции f(x1, ...,xn) называется ДНФ наименьшей длины из всех ДНФ, задающих функцию f(x1, ...,xn). Теорема о кратчайшей ДНФ.Существует кратчайшая ДНФ булевой функции, состоящая из простых импликант. Определение.Простой кратчайшей ДНФ булевой функции f(x1, ...,хn) назовем ее кратчайшую ДНФ, состоящую из простых импликант. Определение. Минимальной ДНФ (МинДНФf) булевой функции f(x1, ...,xn) называется ДНФ наименьшего ранга из всех ДНФ, задающих функцию f(x1, ...,xn). Теорема о минимальных ДНФ.Любая минимальная ДНФ булевой функции состоит из простых импликант. Итак, если булева функция задана матрицей Грея, то: - для построения сокращенной ДНФ необходимо выделить все - для построения кратчайшей ДНФ - их достаточное множество минимальной мощности; - для построения минимальной ДНФ - такое достаточное множество максимальных интервалов, сумма рангов которых минимальна. Определение.ДНФ булевой функции f(x1, ...,xn) называется безызбыточной ДНФ (БезДНФf, если из нее нельзя удалить ни одной конъюнкции и ни одной переменной из конъюнкции так, чтобы она оставалась равносильной исходной ДНФ. В частности, безызбыточной является любая минимальная и любая кратчайшая ДНФ (не простая кратчайшая ДНФ явно избыточна).
21. Метод Закревского получения приближенной кратчайшей ДНФ Существуют различные методы поиска приближенных кратчайших ДНФ, но мы остановимся лишь на одном из них. Как показало его тестирование на функциях небольшого числа аргументов, метод находит чаще всего либо кратчайшую ДНФ, либо отличающуюся от кратчайшей на одну конъюнкцию. Алгоритм Закревского(ориентирован на матричное представление функции и визуальный способ решения). Начало.Задана матрица Грея булевой функции. Шаг 1. Для каждой точки вычислим цену - количество соседних ей точек. Все точки будем считать неотмеченными. Шаг 2. Среди неотмеченных точек рассмотрим точку минимальной цены и найдем все максимальные интервалы, которым она принадлежит. Выберем из них тот максимальный интервал, который содержит наибольшее число неотмеченных точек. Если таких интервалов несколько, то выберем из них интервал максимальной мощности. Шаг 3. Включим выбранный интервал в решение и отметим на матрице его точки. Если не все точки отмечены, то идем на шаг 2. Конец. Включенные в решение интервалы задают приближенную кратчайшую ДНФ.
22. Поиск сокращенной ДНФ: теорема Квайна и алгоритм Квайна-МакКласки. Теорема (Квайна). Чтобы получить сокращенную ДНФ булевой функции из совершенной ДНФ, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций. Опираясь на теорему Квайна, МакКласки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме. Алгоритм Квайна-МакКласки: Начало. Задана совершенная ДНФ булевой функции. Шаг 1. Построим список всех точек функции (булевых векторов) и упорядочим их по неубыванию числа единиц - веса. Шаг 2. Разобьем список на подмножества (классы) векторов одинакового веса. Обозначим через Сi класс векторов веса i. Шаг 3. Выполним неполные склеивания всех соседних векторов классов Ci и Ci+1, i=0,1, ...,n-1. Векторы, участвующие в склеивании (α и β), отметим, а полученные векторы (γ) занесем в новый список и приведем в нем подобные. Шаг 4. Если новый список векторов не пуст, возвратимся с ним на шаг 2 (заметим, что троичные векторы списка оказываются уже упорядоченными по числу единиц). Конец. Выписав из всех списков неотмеченные векторы, получим множество всех максимальных интервалов, оно задает сокращенную ДНФ исходной функции.
Сравнивая алгоритм Квайна-МакКласки с теоремой Квайна, оценим предложения МакКласки. Во-первых, представление конъюнкций булевыми и троичными векторами делает вычисления более простыми и более приспособленными для компьютерной реализации. Во-вторых, разбиение на классы позволяет не искать соседей в тех парах классов, в которых их не может быть, то есть в классах, номера которых отличаются более чем на единицу. В-третьих, отметка склеиваемых соседей (но не вычеркивание их, так как один и тот же вектор может быть соседом нескольким векторам) позволяет свести поглощение к выписыванию неотмеченных векторов. 23. Поиск сокращенной ДНФ: теорема Блэйка и алгоритм Блэйка-Порецкого. Теорема (Блейка).Чтобы получить сокращенную ДНФ булевой функции из произвольной ДНФ, надо выполнить всевозможные обобщенные склеивания смежных конъюнкций, а затем всевозможные поглощения конъюнкций. На основе теоремы Блейка сформулирован алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
, так как при c = 0 `x = x, а при c = 1`x =`x , получим ]
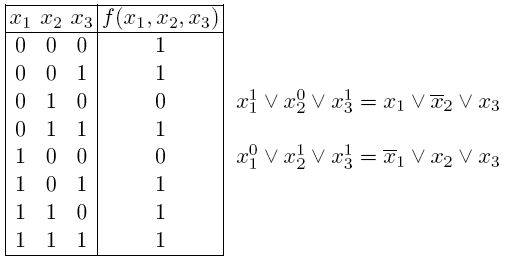
, задающую функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула 
должна задавать функцию, двойственную стрелке Пирса - это штрих Шеффера: в самом деле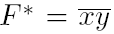 
- это функция НЕ-И, то есть штрих Шеффера.
нужно перевернуть вектор-столбец значений исходной функции 
, a для получения функции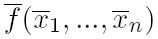 
еще и инвертировать компоненты столбца.
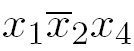, x1x3, x1, 1 - элементарные конъюнкции, a 
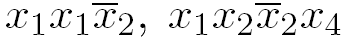не являются элементарными.
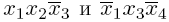ортогональны по переменным x1 и x3.
являются соседними по переменной x3 (ортогональны только по x3 и совпадают по x1 и x2).
являются смежными по переменной x3 (ортогональны только по x3).