|
|
Расширение множества действительных чиселОпределение 2.1. Если множество R (действительных чисел) дополнить символами + 1. 2. 3. 4. Если x>0, то 5. 6. Операции Тогда полученное множество называется расширенным множеством действительных чисел и обозначается
МОДУЛЬ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
Определение 3.1. Модуль (абсолютная величина) действительного числа х обозначается | х| и определяется следующим образом:
Модуль числа х равен расстоянию от точки х до начала отсчёта 0. Свойства модуля Для любого действительного числа х выполняются следующие неравенства и равенства: 1о. Доказательство.
2о. Пусть а>0, тогда Доказательство.
3о. Пусть а>0, тогда 4о. Доказательство.
5о. Доказательство.
6о. 7о. Доказательство 6о и 7о вытекает из правил умножения и деления действительных чисел и Опр.3.1.
ПРОМЕЖУТКИ
Определение 4.1. Пусть a,b – действительные числа, причём a<b. Промежутком (числовым промежутком) называется каждое из следующих множеств отрезок интервал полуинтервал полупрямая (луч) открытая полупрямая (открытый луч) прямая Множество [a;b] называется отрезком с началом a и концом b; (a;b) – интервалом с началом a и концом b; [a;b), (a;b] – полуинтервалом с началом a и концом b; любое число х (a<x<b) называется внутренней точкой этих промежутков. Множества Изобразим эти множества на числовой прямой:
[a;b] [a;a] (a;b) [a;b) (a;b]
Определение 4.2. Окрестностью точки а называется любой интервал, содержащий точку а. Геометрически окрестность изображают следующим образом:
Определение 4.3. Пусть Геометрически
Определение 4.4. Пусть Геометрически
Пример.Построить на координатной прямой U(2; 0,5)
ОГРАНИЧЕННЫЕ И НЕОГРАНИЧЕННЫЕ МНОЖЕСТВА В этом параграфе будем рассматривать только числовые множества и кратко будем называть их «множества». Определение 5.1.Множество Х называется ограниченным сверху (снизу), если существует такое число M (m), что Пример 5.1.Найти верхнюю и нижнюю границы множеств:
Определение 5.2.Множество Х называется ограниченным, если оно ограничено и сверху и снизу, т.е. существуют такие числа M и m , что Это определение равносильно следующему Определение 5.3.Множество Х называется ограниченным, если существует такое число M >0, что Определение 5.4.Наименьшая (наибольшая) из верхних (нижних) границ ограниченного сверху (снизу) множества Х называется верхней (нижней) гранью множества Х и обозначается sup X (inf X), читается supremum (infimum). Свойства верхней и нижней граней множества 1о. Если a* = sup X, то 1) 2) 2о. Если 1) 2) Теорема 5.1.Всякое ограниченное сверху (снизу) множество имеет верхнюю (нижнюю) грань и при том только одну.
Замечание 5.1. Если множество Х неограниченно сверху (снизу), то будем считать sup X =+ В заключение приведем Аксиому Архимеда.Каким бы ни было действительное число k, всегда есть натуральное число n, которое больше k. Из этой аксиомы следует, что множество натуральных чисел неограниченно. Пример 5.2.Найти верхнюю и нижнюю грани множеств:
ДЕЙСТВИТЕЛЬНЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ П.1. Понятие функции На практике мы часто встречаемся с зависимостями между разными величинами. Изучение зависимости между объектами состоит в том, что между ними устанавливается соответствие. Определение 6.1. Соответствие между множествами X и Y, при котором каждому элементу х множества Х соответствует один и только один элемент у множества Y, называется функцией, заданной на множестве X со значением в множестве Y. Функция обозначается при помощи латинской (а иногда греческой) буквы, например, буквы f. Элемент х Î Х называется аргументом или независимой переменной функции f. Множество всех таких элементов х Î Х называют областью определения функции f и обозначают D(f) (D(f) Заметим, что если у Î Е(f), то существует по крайней мере один такой х Î D(f), что f(х) = у. Функцию f, заданную на множестве X со значениями в множестве Y, обозначают также следующим образом:
Определение 6.2. Две функции f и g называют равными (пишут f = g), если D(f) = D(g) и f(х) = g(х) для каждого х Î D(f). Функции называются также отображениями. Если функция f задана на паре множеств Х и Y, т.е. f Ì Х ´ Y, то говорят, что f есть отображение из Х в Y. Если X = D(f) и Е(f) Ì Y, то говорят, что f есть отображение множества Х в Y. Если X = D(f) и Y = Е(f), то говорят, что f есть отображение множества Х на Y. Определение 6.3. Функция f , область определения и область значений которойсостоят из некоторого множества действительных чисел, называется действительной функцией одной действительной переменной. Ниже для краткости будем говорить «функция», подразумевая действительную функцию одной действительной переменной. Функция считается заданной, если выполнены следующие два условия: 1) заданы два числовых множества Х и Y; 2) задан способ (правило), при помощи которого каждому числу х Î Х ставится в соответствие единственное число y Î Y. П.2. Способы задания функции. 1. Аналитический, т. е. с помощью формулы. Если функция задана формулой и не дано дополнительных ограничений, то областью определения функции считают множество всех значений переменной, при которых эта формула имеет смысл. Иногда функция задается в области определения не одной формулой, а несколькими разными формулами. Пример 6.1.Функция
задана аналитическим способом на множестве действительных чисел при помощи трех разных формул. Пример 6.2. Функция Дирихле
Пример 6.3. y=sgn x 2. Табличный способ. 3. Словесный (описывают словами закон, по которому находятся значения функции). Пример 6.4. Функция f каждому квадрату со стороной а ставит в соответствие его площадь.S(a)=a2, a>0. Пример 6.5. Каждому действительному числу х поставим в соответствие наибольшее целое число, которое не превосходит y. Эта функция – Антье, обозначается E(x)=[x], её график.
4. Графами.
5. Графический (только для числовых функций числового аргумента). Определение 6.4. Графиком функции Заметим, для того чтобы некоторое множество точек плоскости являлось графиком какой–либо функции, необходимо, чтобы это множество имело не более одной общей точки с любой прямой, параллельной оси Оу. Рис. 10 Рис. 11 П.3. Основные свойства 1.Монотонныефункции Определение 6.5.Пусть функция
Иначе: функция f называется возрастающей (убывающей) на множестве Е, если большему значению аргумента из этого множества соответствует большее (меньшее) значение функции (рис. 12). Рис.12 Если же для любых значений х1, х2, взятых из некоторого множества Е Ì D(f) и удовлетворяющих условию х1 < х2, вытекает некоторое неравенство f(х1) £ f(х2) (или f(х1) ³ f(х2)), то функция называется неубывающей (невозрастающей) на множестве Е. Пример 6.6. Доказать, что сумма двух возрастающих ( убывающих ) на множестве Е функции есть функция возрастающая ( убывающая) на этом множестве.
2. Функции чётные и нечётные Определение 6.6.Функция 1) 2) Из курса СШ известны чётные функции
нечётные функции
Есть функции, которые не являются ни четными, ни нечетными
Есть функции, которые одновременно являются четными и нечетными
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Пример 6.7. Доказать, что произведение чётной функции на нечётную есть функция нечётная.
3. Периодические функции Определение 6.7. Функция 1) 2) Из курса СШ известны периодические функции Наименьший из положительных периодов называют основным и обозначают Т. Есть периодические функции, для которых нельзя указать основной период. Например,
Пример 6.8. Доказать, что если число l - период функции, то число kl (k=–1, ±2, …) также является периодом.
4. Ограниченные и неограниченные функции Определение 6.8. Функция Определение 6.9. Функция Из курса СШ известны ограниченные функции 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
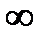и –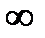 
, и ввести операции «сложения», «умножения», отношение порядка следующим образом:
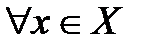выполняется неравенство – 
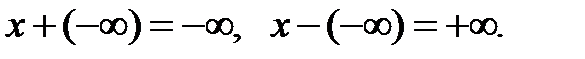
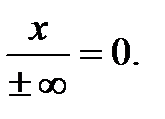
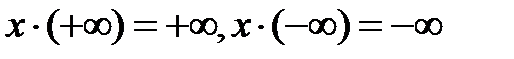; если x<0, то 
.
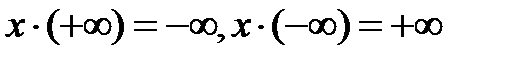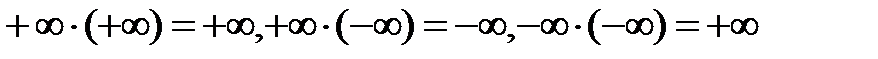
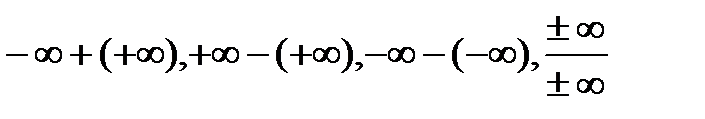неопределенны.
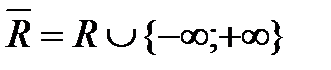или 
.
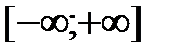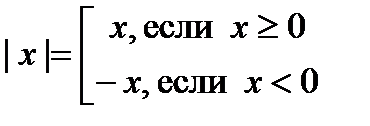
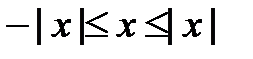
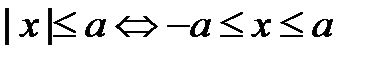
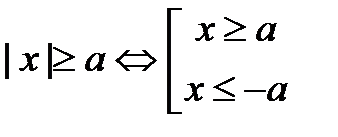
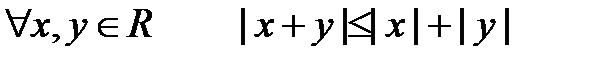
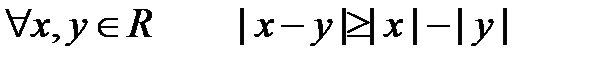
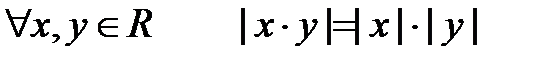
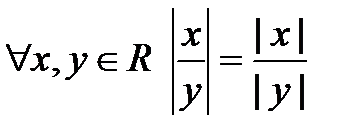
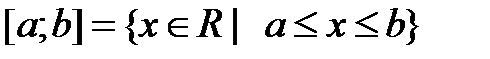
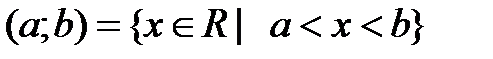
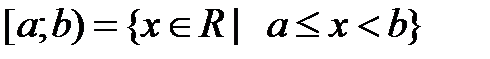или 
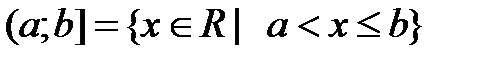
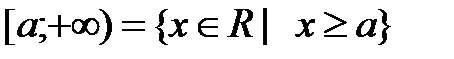
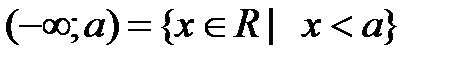или 
или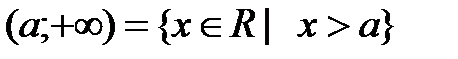 
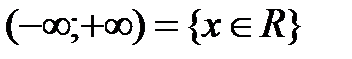
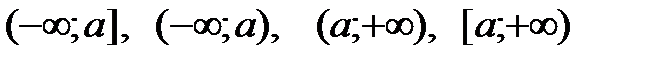называются бесконечными промежутками.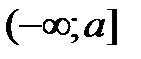
. 
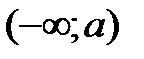
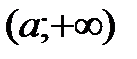
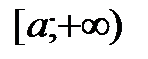
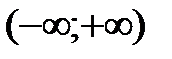
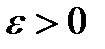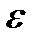-окрестностью точки а называется интервал 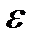(а – 
; а +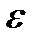 
), т.е. множество всех действительных х, удовлетворяющих неравенству |х – а|< 
. При этом число 
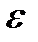называется радиусом окрестности, а точка а – центром окрестности. Обозначают U(a; 
).
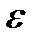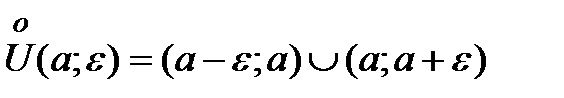
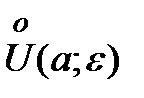изображают следующим образом:
( 
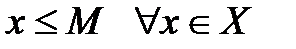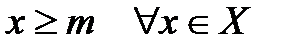). Число M (m), называется верхней (нижней) границей множества Х.
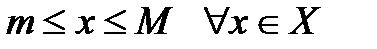. В противном случае оно называется неограниченным.
. Множество Х называется неограниченным, если для любого числа M >0 существует такое числ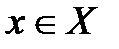о 
, что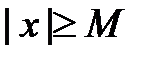 
.
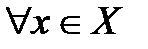выполняется неравенство 
.
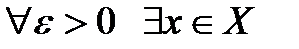такое, что выполняется неравенство 
.
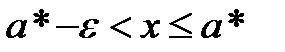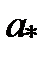= inf X то
.
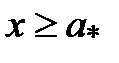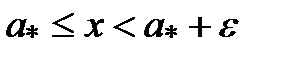
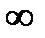(inf X =– 
).
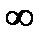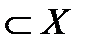). А элемент y Î Y, соответствующий элементу х, называется значением функции f и обозначается f(х). Множество, состоящее из всех значений функции f, называют областью (множеством) значений функции f и обозначают Е(f)(Е(f)
).
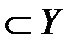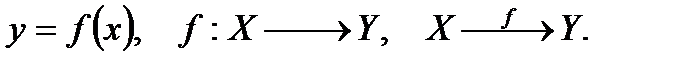
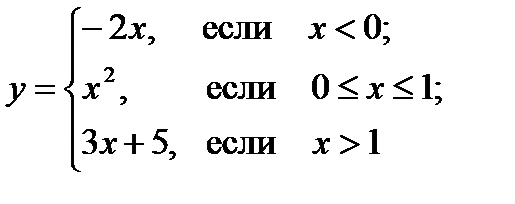
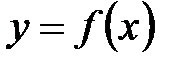, заданной на множестве Х, называется множество всех точек плоскости с координатами 
, где х Î D(f).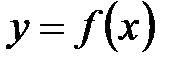
задана на некотором множестве D(f). Данная функция называется возрастающей (убывающей) на множестве Е Ì D(f), если для любых х1 и х2 из множества Е, таких что х1 < х2, выполняется неравенство
.
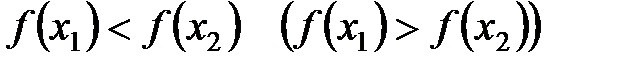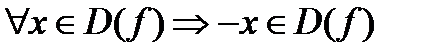т.е.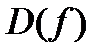 
– симметричное множество относительно 0;
.
.
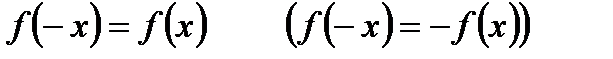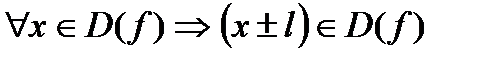
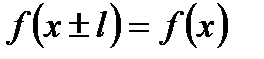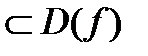, если существует такое число М>0, что для каждой точки из множества Е выполняется неравенство: 
.